10th Maths Question Bank
Chapter 1
Objective Type Question Answer
Q1. Choose the correct option
1. The HCF of `96` and `404` will be
a) `120` b) `4` c) `10` d) `3`
2. The HCF of `12` and `15` will be
a) `3` b) `4` c) `10` d) `5`
3. Product of numbers `= 32` and their LCM `= 8`, then their HCF Will be
a) `4` b) `8` c) `32` d) `256`
4. The HCF of `4` and `7` will be
a) `1` b) `2` c) `3` d) `4`
5. For some integer m, every sum integer is of the form
a) `2m+3` b) `2m + 1` c) `2m` d) `2m+ 5`
6. The rato of LCM and HCF for the numbers `5, 15, 20` Will be
a) `9: 1` b) `4:3` c) `11:1` d) `12:1`
Answer
1(b), 2.(a), 3.(a), 4.(a), 5.(c), 6.(d)
Q2. Fill in the blanks
1) Dividend = divisor×qutient+_____.
2) The value of HCF of the numbers `8,9` and `25` will be______ .
Answer
1. Remainder, 2. 1
Q3. Write True/False
1) Two positive integers a and b, there exist whole numbers q and r satisfying `a = bq+r, 0le r ltb.`
2) A prime factorisation of a natural number is unique apart from the order of its factors
Q4. Answer in one word/sentence
1) Write the HCF of `94` and `404`.
2) For an integer `P, 2p+1` will be even or odd.
Answer
1) 2, 2) Odd.
Ex 1.1
Q1. Use Euclid's division algorithm to find the HCF of `135` and `225`.
Q2. Use Euclid's division algorithm to find the HCF of `867` and `255`.
Q3. An army contingent of `616` members is to march behind an army band of `32` members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Q4. Show that every positive even integer is of the form `2q,` and that every positive odd integer is of the form `2q + 1,` where `q` is some integer.
Q5. Show that any positive odd integer is of the form `4q + 1` or `4q + 3,` where `q` is some integer.
Q6. A sweet seller has `420` kaju barfis and `130` badam barfis. She wants to stack them in such a way that each stack has the same number, and they take up the least area of the tray. What is the number of that can be placed in each stack for this purpose?
Q7. Given positive integers `a` and `b`, there exist unique integers `q` and `r` satisfying `a = bq + r, le 0 lt b`.
for solution click here (Ex 1.1)
Ex 1.2
Q1. Express `140` number as a product of its prime factors.
Q2. Express `156` number as a product of its prime factors.
Q3. Find the `LCM` and `HCF of `12,15` and `21` integers by applying the prime factorisation method.
Q5. Given that `HCF (306, 657)=9`, find `LCM (306, 657)`.
Q6. Explain why `7times11times13+13` and `7times6times5times4times3times2times1=5` are composite numbers.
Q7. Consider the numbers `4^n,` where `n` is a natural number. Check whether there is any value of `n` for which `4^n` ends with the digit zero.
Q8. Find the LCM and HCF of `6` and `20` by the prime factorisation method.
Q9. Find the HCF of `96` and `404` by the prime factorisation method. Hence, find their LCM.
Q10. Find The HCF and LCM of `6, 72` and `120`, using the prime factorisation method.
for solution click here (Ex 1.2)
Chapter 2
Q1. Choose the correct option
1. If `α` and `β` are the zeroes of the quadratic polynomial `ax²+bx+c` then the value of `α.β` is
a) `c/a` b) `a/c` c) `-c/c` d) `-a/c`
2. If α and β are the zeroes of the quadratic polynomial `ax²+bx+c` then the value of `α+β` is
a) `b/a` b) `b/c` c) `-b/a` d) `-a/c`
3. The zero of linear polynomial ax+b is
a) `a/b` b) `b/a` c) `-b/a` d) `-a/c`
4. The zeroes of the polynomial `x²-3` will be
a) `±sqrt3` b) `± 3` c) `3` d) `9`
5. The zeroes of the polynomial `x²+7x+10` will be
a) `2,5` b) `-2,-5` c) `-2,5` d) `2,-5`
6. The degree for the polynomial `(x+1)(x²-x-x⁴+1)` will be
a) `2` b) `3` c) `4` d) `5`
7. If `-3` and `4` are the zeroes of the quadratic polynomial, the quadratic polynomial will be
a) `x²-x-12` b) `x²+x+12` c) `(x²)/2-x/2-6` d) `(x²)/2+x/2-6`
8. The total zeroes of a polynomial are the number of points is equal to the total of the intersection of the diagram of that polynomial on the following
a) On `x`-axis b) On `y`-axis c) On both `x`-axis and `y`-axis d) None of them
Answer
1. a, 2. c, 3. c, 4. a, 5. b, 6. d, 7. a, 8. a
Q2. Fill in the blanks
1. The zeroes of the linear polynomial `ax+b` are ______.
2. The product of two polynomials is a ______.
3. The sum of the zeroes of the polynomial `x²+4x+8` is ______.
4. The product of the zeroes of the polynomial `x²+4x+8` is _____.
5. If `-3` is the zero of the polynomial `(k-1)x²+kx+1`, then the value of `k` will be _____.
Answer
1. `-b/a,` 2. polynomial, 3. `-4,` 4. `8,` 5. `4/3`
Q3. Write true/false
1. Algebraic expression `x²-2√x+7` is not a polynomial.
2. The degree of a zero polynomial is zero.
3. The degree of zero polynomial is undefined.
4. A polynomial of degree n can have at most n zeroes.
Answer
1. True, 2. False, 3. True, 4. True.
Q4. Answer in one word/sentence
1. What is the degree of the linear polynomial?
2. What is the degree of the quadratic polynomial?
3. What is the degree of the cubic polynomial?
4. The graph of `y=p(x)` is in the given figure below, for some polynomials `p(x)`. Find the number of zeroes of `p(x)`.
Answer
1. One, 2. two, 3. three, 4. two.
Ex 2.2
Q1. Find the zeroes of the quadratic polynomial `x^2-2x-8,` and verify the relationship between the zeroes and the coefficients.
Q2. Find the zeroes of the quadratic polynomial `3x^2-x-4,` and verify the relationship between the zeroes and the coefficients.
Q3. Find the zeroes of the quadratic polynomial `x^2+7x+10,` and verify the relationship between the zeroes and the coefficients.
Q4. Find the zeroes of the quadratic polynomial `5t^2+12t+7,` and verify the relationship between the zeroes and the coefficients.
Q5. Find a quadratic polynomial, the sum, and product of its zeroes are `1/4, -1` respectively.
Q6. Find a quadratic polynomial, the sum, and product of its zeroes are `sqrt2, 1/3` respectively.
Q7. Find a quadratic polynomial, the sum, and product of its zeroes are `1` and `1` respectively.
Q8. Find a quadratic polynomial, the sum, and product of its zeroes are `-3` and `2` respectively.
Q9. Find a quadratic polynomial, the sum, and product of its zeroes are `-1/4` and `1/4` respectively.
Q10. Find a quadratic polynomial, the sum, and product of its zeroes are `4` and `1` respectively.
for solution click here (Ex 2.2)
Chapter 3
Q1. Choose the correct option
1. The linear equation in two variables of the following
a) `2x²+3x=5` b) `3x+4y²=6` c) `4x²+5y²=6` d) `5x+6y=7`
2. When `(a_1)/(a_2)≠(b_1)/(b_2),` then the pair of linear equations `a_1x+b_1y+c_1=0` and `a_2x+b_2y+c_2=0`
a) Unique solution b) No solution c) Infinitely many solution d) None of these
3. When `(a_1)/(a_2)=(b_1)/(b_2)≠(c_1)/(c_2)`, then the pair of linear equations `a_1x+b_1y+c_1=0` and `a_2x+b_2y+c_2=0`
a) Unique solution b) No solution c) Infinitely many solution d) None of these
4. When `(a_1)/(a_2)=(b_1)/(b_2)=(c_1)/(c_2),` then the pair of linear equation `a_1x+b_1y+c_1=0` and `a_2x+b_2y+c_2=0`
a) Unique solution b) No solution c) Infinitely many solution d) None of these
5. The pair of the linear equation `a_1x+b_1y+c_1=0` and `a_1x+b_2y+c_2=0` is a condition of having a unique solution
a) `(a_1)/(a_2)=(b_1)/(b_2)` b) `(a_1)/(a_2)=(b_1)/(b_2)≠(c_1)/(c_2)` c) `(a_1)/(a_2)=(b_1)/(b_2)=(c_1)/(c_2)` d) None of these
6. The pair of linear equation `a_1x+b_1y+c_1=0` and `a_2x+b_2y+c_2=0` is a condition of having a no solution
a) `(a_1)/(a_2)=(b_1)/(b_2)` b) `(a_1)/(a_2)=(b_1)/(b_2)≠(c_1)/(c_2)` c) `(a_1)/(a_2)=(b_1)/(b_2)=(c_1)/(c_2)` d) None of these
7. The pair of linear equation `a_1x+b_1y+c_1=0` and `a_2x+b_2y+c_2=0` is a condition of having infinitely many solutions
a) `(a_1)/(a_2)=(b_1)/(b_2)` b) `(a_1)/(a_2)=(b_1)/(b_2)≠(c_1)/(c_2)` c) `(a_1)/(a_2)=(b_1)/(b_2)=(c_1)/(c_2)` d) None of these
Answer
1. d, 2. a, 3. b, 4. c, 5. a, 6. b, 7. c.
Q2. Fill in the blanks
1. In the equation `2x+3y=5` if `x=1` then `y=` _____ .
2. The equation that can be put in the form `ax+by+c=0`, where a, b, and c, are the real numbers and a and b both are non-zero, in two variables `x` and `y` is called a ______ equation.
3. In the equation `2x+y=k,` if `x=2, y=1`, then the value of k will be_____.
Answer
1. 1, 2. Linear, 3. 5.
Q3. Write true/false
1. A linear equation has many solutions in two variables.
2. Every solution of a linear equation is a point on the line representing it is.
Answer
1. True, 2. True.
Q4. Answer in one word/sentence
1. Write the standard form of the linear equation in two variables.
2. In the linear equation `y=mx+3`, if `x=2, y=5,` then what will be the value of `m`?
Answer
1. `ax²+bx+c=0`, 2. `-1`.
Ex 3.2
Q1.`5` pencils and `7` pens together cost `₹50`, whereas `7` pencils and `5` pens together cost `₹46`. Find the cost of one pencil and that one pen.
for solution click here (Ex 3.2)
Ex 3.3
Q1. Solve the pair of linear equations
`x+3y=6`
`2x-3y=12`
by the substitution method.
Q2. Solve the pair of linear equations
`x-2y=0`
`3x+4y=20`
by the substitution method.
Q3. Solve the pair of linear equations
`7x-15y=2`
`x+2y=3`
by the substitution method.
Q4. Solve `2x+3y=11` and `2x-4y=-24` and hence find the value of `'m'` for which `y=mx+3`.
Q5. Form the pair of linear equations for the following problems and find their solution by substitution method.
Q6. The difference between two numbers is `26` and one number is three times the other. Find them.
Q7. The larger of two supplementary angles exceeds the smaller by `18` degrees. Find them.
Q8. The coach of a cricket team buys `7` bats and `6` balls `₹3800`. Later, she buys `3` bats and 5 balls for`₹1750`. Find the cost of each bat and each ball.
for solution click here (Ex 3.3)
Ex 3.4
Q1. Solve the pair of linear equations
`3x-5y-4=0`
`9x=2y+7`
by the elimination method.
Q2. The ratio of incomes of two persons is `9 : 7` and the ratio of their expenditures is `4 : 3.` If each of them mangoes to save `₹ 2000` per month, find their monthly incomes.
Q3. The sum of a two-digit number and the number obtained by reversing the digits is `66.` If the digits of the number differ by `2,` find the number. How many such numbers are there?
for solution click here (Ex 3.4)
Ex 3.5
Q1. Solve the pairs of linear equations
`2x+y=5`
`3x+2y=8`
has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method.
Q2. For which value of `k` will the following pair of linear equations have no solution?
`3x+y=7`
`(2k-1)x+(k-1)y=2k+1`
Q3. The cost of `5` oranges and `3` apples is `₹ 35` and the cost of `2` oranges and `4` apples `₹28`. Let us find the cost of an orange and an apple.
Q4. For which values of `p` does the pair of equations given below has unique solution?
`4x+py+8=0`
`2x+2y+2=0`
Q5. For what values of `k` will the following pair of linear equations have infinitely many solutions?
`kx+3y-(k-3)=0`
`12x+ky-k=0`
for solution click here (Ex 3.5)
Chapter 4
Q1. Choose the correct option
1. If the quadratic equation `ax²+bx+c=0` has the same roots, then the value of the discriminant of the equation will be
a) `0` b) `1` c) `2` d) `3`
2. The nature of the roots of the equation `x²+x-1=0` will be
a) Real and equal b) Real and different c) No real root d) None of these
3. The maximum power of the variable in a quadratic equation is
a) `1` b) `2` c) `3` d) `4`
4. The discriminant of the quadratic equation `ax²+bx+c` will be
a) `D=b²-4ac` b) `D=4ac-b²` c) `D=b³-4ac` d) `D=4ac-b³`
5. Which of the following of the quadratic equation have real roots
a) `x²+9x+4=0` b) `x²-4x+5=0` c) `x²+x+2=0` d) `x²+5x+8=0`
6. The roots of the quadratic equation `2x²-7x+6=0` will be
a) `3/2, 2` b) `-3/2, -2` c) `-3/2, 2` d) `3/2, -2`
Answer
1. a, 2. b, 3. b, 4. a, 5. a, 6. a
Q2. Fill in the blanks
1. The equation `p(x)=0`, where `p(x)` is the polynomial of degree `2`, the equation is called _____.
2. A quadratic equation has maximum ______ roots.
3. The roots of the equation `(x-3)(x+4)=0` are _____ .
4. If the roots of a quadratic equation are real and equal, then the value of the discriminant of that equation, `D=` ______.
Answer
1. Quadratic, 2. two, 3. 3, `-4,` 4. zero, 5. `b²=4ac`.
Q3. Write true/false
1. A quadratic equation can have more than one root.
2. The roots of equation `x(x-1)=0` will be `0` and `-1`.
3. The roots of the equation `2x²-4x+4=0` will be equal.
4. `ax+b=0` is a quadratic equation.
Answer
1. False, 2. False, 3. True, 4. False.
Q4. Answer in one word/sentence
1. What is called the value `b²=4ac` in the equation `ax²+bx+c=0.`
2. If the roots of a quadratic equation are real and equal, then what will be the value of the discriminant of that equation?
3. If the value of the discriminant of an equation is negative, then what will be the nature of the roots of that equation?
4. If the value of the discriminant of an equation is positive, then what will be the nature of the roos of that equation?
Answer
1. discriminant, 2. zero, 3. roots are not real, 4. roots are real and different.
Ex 4.1
Q1. Check whether the equation `x^3-4x^2-x+1=(x-2)^3` is a quadratic equation or not.
Q2. Check whether the equation `(2x-1)(x-3)=(x+5)(x-1)` is a quadratic equation or not.
Q3. Check whether the equation `(x+2)^3=2x(x^2-1)` is a quadratic equation or not.
Q4. Represent the following situations in the form of quadratic equations :
A train travels a distance of `480`km at a uniform speed. If the speed had been `8`km/hr less, then it would have taken `3` hours more to cover the same distance, we need to find the speed of the train.
Q5. Represent the following situations in the form of quadratic equations :
The product of two consecutive positive integers is `306` we need to find the integers.
for solution click here (Ex 4.1)
Ex 4.2
Q1. Find the roots of the quadratic equation `sqrt2x^2+7x+5sqrt2=0,` by factorisation.
Q2. Find the roots of the quadratic equation `2x^2-x+1/8=0` by factorisation.
Q3. Find the roots of the quadratic equation `2x^2-7x+3=0` by factorisation.
Q4. A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in`₹`) was found to be `55` minus the number of toys produced in a day. On a particular day, the total cost of production was `₹750`. Find out the number of toys produced on that day.
for solution click here (Ex 4.2)
Ex 4.3
Q1. The diagonal of a rectangular field is `60` metres more than the shorter side. If the longer side is `30` metres more than the shorter side, find the sides of the field.
Q2. The difference of square of two numbers is `180`. The square of the smaller number is `8` times the larger number. Find the two numbers.
Q3. A train travels `360`km at a uniform speed. If the speed had been `5`km/h more, it would have taken `1` hour less for the same journey. Find the speed of the train.
Q4. Two water taps together can fill a tank in `9(3)/8` hours. The tap of larger diameter takes `10` hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Q5. Sum of the areas of two squares is `468m^2`. If the difference of their perimeters is `24m`, find the sides of the two squares.
for solution click here (Ex 4.3)
Ex 4.4
Q1. Find the values of `k` for quadratic equations `2x^2+kx+3=0`, so that they have two equal roots.
Q2. Find the values of `k` for quadratic equations `kx(x-2)+6=0`, so that they have two equal roots.
Q1. Choose the correct option
1. For the A.P. ___,___ write the first term and common difference respectively
a) `3/2, -1` b) `-3/2, 1` c) `-3/2, -1` d) `3/2, 1`
2. The `30th` term of the A.P. `10, 7, 4`, __,__,__ is
a) `97` b) `77` c) `-77` d) `-87`
3. The 11th term of the A.P. `-3, -1/2, 2,`__,__, is
a) `28` b) `22` c) `-38` d) `(-48)1/2`
4. Which term of `A.P. 3, 6, 9,`__, is `27`.
a) fifth b) eighths c) ninth d) sixth
5. The `11th` term of the series `-5, -5/2, 0, 5/2,`__, will be.
a) `-20` b) `20` c) `-30` d) `30`
Answer
1. a, 2. c, 3. b, 4. c, 5. b
Q2. Fill in the blanks
1. In an `A.P. 3/2, 1/2, -1/2, 3/2,`___, the common difference `'d'` is ___.
2. The `nth` term of an `A.P.` is `3+2n` then the first term will be___.
Answer
1. -1, 2. 5
Q3. Write true/false
1. `-2, 2, -2, 2, -2,`__ is an `A.P`.
2. If `a, b, c,` is in `A.P.` then `b=(a+c)/2`.
3. `6th` term of `A.P. 8, 6, 4,`___, is `-2`.
Answer
1. False, 2. True, 3. True.
Q4. Answer in one word/sentence
1. Write the value of the `10th` term of an `A.P. 2, 7, 12`,____.
2. Give the number of `10th` term of an `A.P. 4, 6, 8`,____.
Answer
1. 47, 2. 19.
Ex 5.2
Q1. Which term of the AP : `21, 18, 15,` .... is `-81` ? Also, is any term `0`? Give reason for your answer.
Q2. Determine the AP whose 3rd term is `5` and the 7th term is `9`.
Q3. Check whether `301` is a term of the list of numbers `5, 11, 17, 23`, .......
Q4. How many two-digit numbers are divisible by `3`?
Q5. Find the 11th term from the last term (towards the first term) of the AP: `10, 7, 4`, .... ,`-62`.
Q6. In a flower bed, there are `23` rose plants in the first row, `21` in the second, `19` in the third, and so on. There are `5` rose plants in the last row. How many rows are there in the flower bed?
Q7. Which term of the AP: `3, 8, 18,` ...., is `78`?
Q8. Find the number of terms of the following AP :`7, 13, 19, ...,205`
Q9. Check whether `-150` is a term of the AP: `11, 8, 5, 2.... .`
Q10. Find the `31`st term of an AP whose `11`th term is `38` and the `16`th term is `73`.
Q11. If the `3`rd and the `9`th terms of an AP are `4` and `-8` respectively, which term of this AP is zero.
Q12. Which term of the AP: `3, 15, 27, 39,...` will be `132` more than its `54`th term?
Q13. How many three-digit numbers are divisible by `7`?
Q14. How many multiples of `4` lie between `10` and `250`?
Q15. Determine the AP whose third term is `16` and the `7`th term exceeds the `5`th term by `12`.
for solution click here (Ex 5.2)
Chapter 6
Q1. Choose the correct option
1. If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. This statement is known as by the following
a) Basic proportionality theorem
b) Pythagoras theorem
c) RHS theorem
d) None of them
2. In `△ABC, AB =6√3 cm`, `AC = 12 cm` and `BC = 6 cm`, then the value of `LB` will be
a) `120°` b) `60°` c) `90°` d) `45°`
3. In any `△ABC, DE∥AE` and `CD = 3 cm, EC = 4 cm, BE = 6 cm` then `DA` will be
a) `7.5 cm` b) `3 cm` c) `4.5 cm` d) `6 cm`
4. If in a triangle, the square of a side is equal to the sum of the squares of the other two sides, then the opposite angle to the thinner side will be
a) `90°` b) `60°` c) `180°` d) `45°`
5. In any triangle `△ABC, DE∥BC, AD = x, DB = (x-2), AE = (x+2)` and `EC = (x-1)`, then the value of `x` will be
a) `5` b) `4` c) `3` d) `2`
Answer
1. a, 2. c, 3. c, 4. a, 5. b.
Q2. Fill in the blanks
1. All circles are ___. ( congruent, similar)
2. All squares are ____. ( similar, congruent)
3. All ___ triangles are similar. ( isosceles, equilateral)
4. The ratio of any two corresponding sides in two equiangular triangles is always the ____.
5. If a line divides any two sides of a triangle in the same ratio, then the line is ____ to the third side.
Answer
1. similar, 2. similar, 3. equilateral, 4. same, 5. parallel.
Q3. Write true/false
1. If in two triangles, corresponding angles are equal then their corresponding sides are in the same ratio or proportion and hence the two triangles are similar.
2. If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.
3. In a right triangle, the square of the hypotenuse is equal to the difference of the squares of the other two sides.
4. In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
Answer
1. True, 2. True, 3. False, 4. True.
Q4. Answer in one word/sentence
1. Are all isosceles triangles are similar?
2. Are all squares similar?
Answer
1.No, 2. Yes.
Ex 6.1
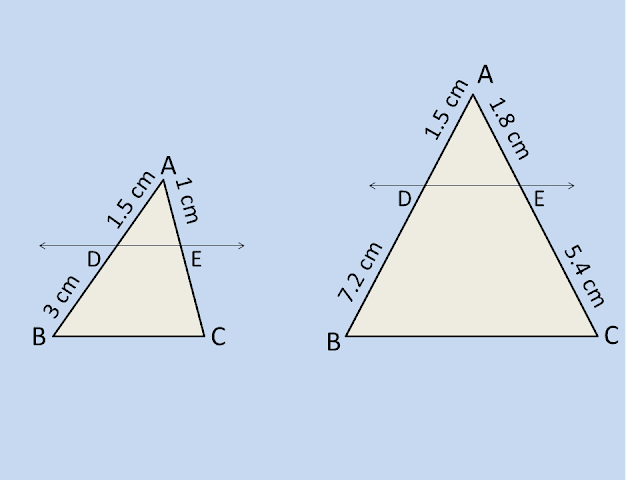
Q1. If a line intersects sides `AB` and `AC` of a `triangleABC` at `D` and `E` respectively and is parallel to `BC`, prove that `(AD)/(AB) = (AE)/(AC).`
Q2. In figure `(PQ)/(SQ) = (PT)/(TR)` and `angle PST = angle PQR.` Prove that `PQR` is an isosceles triangle.
Ex 6.2
Q1. In the figure i) and ii) `DE∥BC.` Find the `EC` in (i) and `AD` in (ii).
Q2. `ABCD` is a trapezium in which `AB∥DC` and diagonals intersect each other at the point `O`. Show that `(AO)/(BO)=(CO)/(DO)`.
Q3. In figure, if `AD ⊥ BC,` prove that `AB^2 + CD^2 = BD^2 + AC^2.`
Ex 6.5
Q1. A ladder `10 m` long reaches a window `8m` above the ground. Find the distance of the foot of the ladder from base of the wall.
Q2. A guy wire attached to a vertical pole of height `18m` is `24 m` long and has a stake attached to other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Chapter 7
Q1. Choose the correct answer
1. The coordinate of the origin point
a) `(x, y)` b) `(x, 0)` c) `(0, y)` d) `(0, 0)`
2. The coordinates of a point on the `x`-axis at a distance of `4` units from the origin will be
a) `(0, 4)` b) `(4, 0)` c) `(0, y)` d) `(0, 0)`
3. The distance between points A(x₁, y₁) and B(x₂, y₂) is
a) `AB=sqrt((x₂-x₁)²+(y₂-y₁)²)`
b) `AB=sqrt((x₂+x₁)²+(y₂+y₁)²)`
c) `AB=sqrt((x₂-x₁)²-(y₂-y₁)²)`
d) `AB=sqrt((x₂-y₂)²-(x₁-y₁)²)`
4. The distance between the points `(8, 6)` and `(0, 0)` is
a) `4sqrt(2)` b) `10` c) `sqrt10` d) `sqrt14`
5. The mid-point of the line segment joining the points `A (x₁, y₁)` and `B(x₂, y₂)` is
a) `(x₁+x₂)/2, (y₁+y₂)/2`
b) `(x₁-x₂)/2, (y₁+y₂)/2`
c) `(x₁+x₂)/2, (y₁-y₂)/2`
d) `(x₁-x₂)/2, (y₁-y₂)/2`
6. The mid-point of the line segment joining points `A(1, 2)` and `B(3, 4)` is
a) `(2, 3)` b) `(3, 2)` c) `(0, 0)` d) `(4, 4)`
Answer
1. d, 2. b, 3. a, 4. b, 5. a, 6. a.
Q2. Fill in the blanks
1. The coordinates of the ends of a diameter of a circle are `(-3, 4)` and `(3, -4)`. Then the coordinate of its center will be ____.
2. Point `(4, 5)` lies in ____.
Answer
1. `(0, 0)`, 2. First.
Q3. Write True/False
1. If the abscissa of a point is zero and the ordinate is 3 then it will lie on the `x`-axis.
2. The coordinate of a point on the y-axis at a distance of `10` units from the origin will be `(10, 0)`.
3. The distance of a point `P(x, y)` from the origin in `sqrt(x²+y²).`
4. The coordinates of the point on the `y`-axis `(0, y)` are of the form.
Answer
1. False, 2. False, 3. True, 4. True.
Q4. Answer in one word/sentence
1. What will be the distance of point `A(3, 4)` from the origin?
2. What will be the coordinate of the midpoints of the line joining the points `A(-1, 2)` and `B(3, 4)`?
3. What will be the distance between the points `(-3, 4)` and `(2, 3)`?
Answer
1. 5, 2. (1, -1) 3. -1.
Ex 7.1
Q1. Find a relation between `x` and `y` such that the point `(x, y)` is equidistant from the points `(7, 1)` and `(3, 5)`.
Q2. Find the distance between the `(2, 3), (4,1)`.
Q3. Find the distance between the `(-5,7), (-1, 3)`.
Q4. Find the distance between the `(a, b), (-a, -b)`.
Q5. Find a relation between `x` and `y` such that the point `(x, y)` is equidistant from the point `(3, 6)` and `(-3, 4)`.
for solution click here (Ex 7.1)
Ex 7.2
Q1. Find the coordinates of the point which divides the line segment joining the points `(4, -3)` and `(8, 5)` in the ratio `3:1` internally.
Q2. In what ratio does the point `(-4, 6)` divide the line segment joining the points `A(-6, 10)` and `B(3, -8)`?
Q3. Find the ratio in which the `text{y-axis}` is divides the line segment joining the points `(5, -6)` and `(-1, -4). Also find the point of intersection.
Q4. If the points `text{A(6, 1), B(8,2), C(9,4)}` and `text{D(p, 3)}` are the vertices of a parallelogram, taken in order, find the value of `p`.
for solution click here (Ex 7.2)
Ex 7.3
Q1. Find the area of a triangle whose vertices are `(1, -1), (-4, 6),` and `(-3, -5)`.
Q2. Find the area of a triangle formed by the points `text{A(5, 2), B(4, 7)}` and `text{C(7, -4)}`.
Q3. Find the value of `k` if the point `text{A(2, 3)), B(4, k)}` and `text{C(6, -3)}` are collinear.
Q4. Find the area of the triangle whose vertices are `(2, 3), (-1, 0),` and `(2, -4)`.
Q5. Find the area of the triangle whose vertices are `(-5, -1), (3, -5)` and `(5, 2)`.
Q6. Find the value of `k`, for which the points are collinear `(7, -2), (5, 1), (3, k)`.
Q7. Find the value of `k`, for which the points are collinear `(8, 1), (k, -4), (2, -5)`.
for solution click here (Ex 7.3)
Chapter 8
Q1. Match the column
Column A_________ ____column B
1. `sin theta` ________________i) `sqrt3`
2. `sec theta.cos theta`_____________ii) `text{perpendicular}/text{hypotenuse}`
3. `tan30°`______________iii) `1`
4. `cot theta`____________iv) `1/sqrt3`
5. `sec(90 - theta)`_______v) `sqrt(cosec² theta - 1)`
vi) `cosec theta`
2. `sec theta.cos theta`_____________ii) `text{perpendicular}/text{hypotenuse}`
3. `tan30°`______________iii) `1`
4. `cot theta`____________iv) `1/sqrt3`
5. `sec(90 - theta)`_______v) `sqrt(cosec² theta - 1)`
vi) `cosec theta`
Answer
1. ii, 2. iii, 3. iv, 4. v, 5. vi.
Q2. Match the column
Column A_________ ____column B
1. `cosec 60°`_______________ i) `1`
2. `tan (90 - theta)`__________ ii) `∞`
3. `sin48°sec42°+cos48°cosec42°`_ iii) `2/sqrt3`
4. `sin² theta + cos² theta`______ iv) `cot theta`
5. `tan90°`__________________ v) `2`
Answer
1. iii, 2. iv, 3. v, 4. i, 5. ii
Q3. Match the column
Column A_________ ____column B
1. `sec²3theta-tan²3theta`_________i) `cot² theta`
2. `2tan theta cot theta`___ii) `sec theta`
3. `1+tan² theta`_________iii) `1`
4. `cosec² theta-1`_________iv) `2`
5. `cosec (90-theta)`_____v) `sec² theta`
Answer
1. iii, 2. iv, 3. v, 4. i, 5. ii
Q4. Match the column
Column A_________ ____column B
1. `1+cot² theta`_________i) `cosec theta`
2. `sec theta`___________ii) `0`
3. `sin² theta+cos² theta`___iii) `sqrt3`
4. `tan 60°`_____________iv) `1`
5. `sec(90-theta)`_______v) `cosec² theta`
vi) `1/(cos theta)`
vii) `1/sqrt3`
Answer
1. v, 2. vi, 3. iv, 4. iii, 5. i
Q5. Match the column
Column A_________ ____column B
1. `1+tan² theta`___________i) `cosec² theta`
2. `tan(90-theta)`__________ii) `sec² theta`
3. `sqrt(1-cos² theta)`____________iii) `1/sqrt2`
4. `1+cot² theta`____________iv) `cot theta`
5. `sin 45°`________________v) `sin theta`
Answer
1. ii, 2. iv, 3. v, 4. i, 5. iii
Q6. Match the column
Column A_________ ____column B
1. `sin 60°`_______________i) `sec² theta`
2. `1+tan² theta`___________ii) `sqrt3/2`
3. `1/sec theta`___________iii) `cot² theta`
4. `cos² theta + sin² theta`____iv) `cos theta`
5. `cosec² theta - 1`_________v) `1`
Answer
1. ii, 2. i, 3. iv, 4. v, 5. iii
Ex 8.1
Q1. Given `tan A = 4/3,` find the other trigonometric ratios of the angle `A`.
Q2. In `triangle ABC`, right-angled at `B`, `AB=24 cm, BC=7 cm`. Determine: i) sin `A`, cos `A`
Q3. If `sin A=3/4,` calculate `cos A` and `tan A.`
Q4. Given `15 cot A=8,` find `sin A` and `sec A`.
Q5. Given `sec theta=13/12,` calculate all other trigonometric ratios.
for solution click here (Ex 8.1)
Ex 8.2
Q1. Evaluate `sin 60^circ cos 30^circ + sin 30^circ cos 60^circ`
Q2. Evalutae `2 tan^2 45^circ + cos^2 30^circ - sin^2 60circ`
for solution click here (Ex 8.2)
Ex 8.3
Q1. Evaluate `(tan65^circ)/(cot25^circ)`
Q2. If `sin 3A = cos(A - 26^circ),` where `3A` is an acute angle, find the value of `A`.
Q3. Express `cot 85^circ + cos 75^circ` in terms of trigonometric ratios of angles between `0^circ` and `45^circ`.
Q4. Show that: `tan 48^circ tan23^circ tan42^circ tan 67^circ = 1`
Q5. Show that: `cos 38^circ cos 52^circ - sin 38^circ sin 52^circ =0`
Q6. If `tan 2A = cot(A - 18^circ),` where `2A` is an acute, angle find the value of `A.`
Q7. If `tan A = cot B,` prove that `A + B = 90^circ.`
Q8. If `sec 4A = cosec (A - 20^circ),` where `4A` is an acute angle, find the value of `A.`
Q9. If `A, B` and `C` are interior angles of a triangle `ABC,` then show that `sin((A + B)/2) = cos A/2`
Q10. Express `sin 67^circ + cos 75^circ` in terms of trigonometric ratios of angles between `0^circ` and `45^circ.`
for solution click here (Ex 8.3)
Ex 8.4
Q1. Evaluate: `(sin^2 63^circ + sin^2 27^circ)/(cos^2 17^circ + cos^2 73^circ)`
Q2. Evaluate: `sin 25^circ cos 65^circ + cos 25^circ sin 65^circ`
Q3. Prove that `(1 + sec A)/sec A = sin^2 A/(1 - cos A)` [Hint: Simplify `LHS` and `RHS` separately]
Q5. Prove that `sqrt((1 - sin A)/(1 + sin A)) = sec A - tan A`
for solution click here (Ex 8.4)
Chapter 10
Q1. Choose the correct option
1. `A `tangent `PQ` at a point `P` of a circle of radius `5` cm meets a line through the center `O` at a point `Q` so that `OQ = 12 cm`. Length of `PQ` is
a) `12 cm` b) `13 cm` c) `8.5 cm` d) `sqrt(119) cm`
2. The length of a tangent to a circle from a point `Q` is `24 cm` and the distance of `Q` from the center is `25 cm`. What is the radius of the circle?
a) `7 cm` b) `12 cm` c) `15 cm` d) `24.5 cm`
3. If the tangents `PA, PB` from a point `P` to a circle with center `O` are inclined at an angle of `180°`
Q2. Fill in the blanks.
Q3. Write True/False
Q4. Answer the one-word/sentence.
1. What is the line intersection of two points of a circle?
2. What is the name of the line intersecting a circle at only one point?
Answer
1. secant line, 2. Tangent.
Ex 10.2
Q1. The tangent at any point of a circle is perpendicular to the radius through the point of contact.
Q2. The lengths of tangents drawn from an external point to a circle are equal.
Q3. Prove that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
Q4. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Q5. The length of a tangent from a point `A` at distance `5 cm` from the centre of the circle is `4 cm.` Find the radius of the circle.
Q6. Two concentric circles are of radii `5 cm` and `3 cm.` Find the length of the chord of the larger circle which touches the smaller circle.
for solution click here (Ex 10.2)
Chapter 11
Ex 11.1
Q1. Draw a line segment of length `text {7.6 cm}` and divide it in the ratio `5:8`. Measure the two parts.
Q2. Construct a triangle of sides `text{4 cm, 5 cm}` and `text{6 cm}` and then a triangle similar to it whose sides are `2/3` of the corresponding sides of the first triangle.
Q3. Construct a triangle with sides `text{5 cm, 6 cm}` and `text{7 cm}` and then another triangle whose sides are `7/5` of the corresponding sides of the first triangle.
Q4. Construct an isosceles triangle whose base is `text{8 cm}` and altitude `text{4 cm}` and then another triangle whose sides are `1(1)/2` times the corresponding sides of the isosceles triangle.
Q5. Draw a triangle `text{ABC}` with side `text{BC = 6 cm, AB = 5 cm}` and `angle textABC = 60}^circ`. Then construct a triangle whose sides are `3/4` of the corresponding sides of the triangle `text{ABC}`.
Q6. Draw a triangle `text{ABC}` with side `text{BC = 7 cm, } angle text{B = 45}^circ, angle text{A = 105}^circ.` Then, construct a triangle whose sides are `4/3` times the corresponding sides `triangle text{ABC}`.
Q7. Draw a right triangle in which the sides (other than hypotenuse) are of lengths `text{4 cm}` and `text{3 cm}`. Then construct another triangle whose sides are `5/3` times the corresponding sides of the given triangle.
Q8. Construct a triangle similar to a given triangle `text{ABC}` with its side equal to `3/4` or the corresponding sides of the triangle `text{ABC}`(i.e. of scale factor `3/4`).
Chapter 12
Q1. Choose the correct option
1. If the area of a circle is `154 cm²`, then its perimeter will be
a) `11 cm` b) `22 cm` c) `44 cm` d) `55 cm`
2. If the perimeter and the area of a circle are equal numerically then the radius of that circle is
a) `2 unit` b) `π unit` c) `4 unit` d) `7 unit`
3. What is the area of the sector of a circle having its radius R and whose angle is P
a) `p/(180)×2πR` b) `p/(180)×2πR²` c) `p/(360)×2πR` d) `p/(720)×2πR²`
Answer
1. c, 2. a, 3. d
Q2. Fill in the blanks.
1. If the area of a circle is `4π cm²` then its radius will be ___.
Answer
1. 2 cm.
Q3. Write True/False
1. Circumference of a circle `= 2πr`, where r is the radius of the circle.
2. Area of a circle `= πr²`, where r is the radius of the circle.
3. Area of the sector of the circle `= πr²×theta/(360°)`, where r is the radius of a circle and `theta` is the angle subtended at the center of the circle.
Answer
1. True, 2. True, 3. True
Q4. Answer the one-word/sentence.
1. Write the formula of the area of a circle.
2. Write the formula of the area of the sector.
Answer
1. `πr²`, 2. `πr²×theta/(360°)`.
Ex 12.1
Q1. The cost of fencing a circular field at the rate of `text{₹ 24}` per metre is `text{₹ 5280}`. The field is to be ploughed at the rade of `text{₹ 0.50 per m}^2`. Find the cost of ploughing the field (Take `pi = 22/7`).
Q2. The radii of two circles are `text{19 cm}` and `text{9 cm}` respectively. Find the radius of the circle which has circumference equal to the sum of the circumferences of the two circles.
Q3. The radii of two circles are `text{8 cm}` and `text{6 cm}` respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.
Q4. The wheels of a car are of diameter `text{80 cm}` each. How many complete revolutions does each wheel make in `text{10 minutes}` when the car is travelling at a speed of `text{66 km per hour}`?
Ex12.2
Q1. Find the area of the sector of a circle with radius `text{4 cm}` and of angle `30^circ`. Also, find the area of the corresponding major sector (Use `pi = 3.14`).
Q2. Find the area of a sector of a circle with radius `text{6 cm}` if angle of the sector is `60^circ`.
Ex12.3
Q1. Find the area of the shaded region in figure, where `text{ABCD}` is a square of side `text{14 cm}`.
Q2. Find the area of the shaded region in Figure, if `text{PQ = 24 cm, PR = 7 cm}` and `text{O}` is the centre of the circle.
Q3. Find the area of the shaded region in Figure, if radii of the concentric circles with centre `text{O}` are `text{7 cm}` and `text{114 cm}` respectively and `angle text{AOC = }40^circ.`
Q4. Find the area of the shaded region in Figure, if `text{ABCD}` is a square of side `text{14 cm}` and `text{APD}` and `text{BPC}` are semicircles.
Chapter 13
Q1. Write True/False
1. The total surface area of the hemisphere is `3πr²`, where `r` is the radius of the hemisphere.
2. The volume of the cone is `1/3πr²h`, where r is the radius of the base and `h` is the height of the cone.
Answer
1. True, 2. True.
Q2. Answer in one word/sentence
1. Write the formula of the total surface area of a cuboid.
2. Write the formula of the volume of the cuboid.
3. Write the formula of the total surface area of the sphere.
4. Write the formula of the volume of the sphere.
5. Write the formula of the curved surface area of the hemisphere.
6. Write the formula of the total surface area of the hemisphere.
7. Write the formula of the volume of the hemisphere.
8. Write the formula of the curved surface area of the cylinder.
9. Write the formula of the total surface area of the cylinder.
10. Write the formula of the volume of the cylinder.
11. Write the formula of the curved surface area of the cone.
12. Write the formula of the total surface area of the cone.
13. Write the formula of the volume of the cone.
Answer
1. `TSA` of cuboid `= 2(lb+bh+hl)`, where `l,b,h` are the length, breadth and height respectively.
2. Volume of Cuboid `=lbh`, where `l,b,h` are the length, breadth, and height respectively.
3. `TSA` of the sphere `= 4πr², where `r` is the radius of the sphere.
4. The volume of the sphere `= 4/3πr³`, where `r` is the radius of the sphere.
5. `CSA` of the hemisphere `= 2π²`, where `r` is the radius of the hemisphere.
6. `TSA` of the hemisphere `= 3πr²`, where r is the radius of the hemisphere.
7. The volume of the hemisphere `= 2/3πr²`, where `r` is the radius of the hemisphere.
8. `CSA` of the cylinder `= 2πrh`, where `r` of the base and `h` is the height of the cylinder.
9. `TSA` of the cylinder `= 2πr(r+h)`, where `r` of the base and `h` is the height of the cylinder.
10. The volume of the cylinder `= πr²h`, where `r` of the base and `h` is the height of the cylinder.
11. `CSA` of the cone `= πrl`, where `r` of the base and `l` is the slant height of the cone.
12. `TSA` of the cone `= πr(r+l)`, where `r` of the base and `l` is the slant height of the cone.
13. The volume of the cone `= 1/3πr²h`, where `r` of the base and `h` is the height of the cone.
Ex 13.1
Q1. `2` cubes each of volume `text{64 cm}^3` are joined end to end. Find the surface area of the resulting cuboid.
Q2. A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is `text{14 cm}` and the total height of the vessel is `text{13 cm}`. Find the inner surface area of the vessel.
Q3. A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (see figure). The length of the entire capsule is `text{14 mm}` and the diameter of the capsule is `text{5 mm}`. Find its surface area.
Q4. A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Figure. If the height of the cylinder is `text{10 cm}`, and its base is of radius `text{3.5 cm,}` find the total surface area of the article.
for solution click here (Ex 13.1)
Ex 13.2
Q1. A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to `text{1 cm}` and the height of the cone is equal to its radius. Find the volume of the solid in terms of `pi`.
Q2. A cone of height `24 text{cm}` had radius of base `6 text{cm}` is made up of modelling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere.
for solution click here (Ex 13.2)
Ex 13.3
Q1. Metallic spheres of radii `text{6 cm, 8 cm}` and `text{10 cm,}` respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
Q2. How many silver coins, `text{1.75 cm}` in diameter and of thickness `text{2 mm}`, must be melted to form a cuboid of dimensions `text{5.5 cm}times text{10 cm} times text{3.5 cm}`?
for solution click here (Ex 13.3)
Chapter 14
Q1. Choose the correct option
1. The relation between the median, mode, and mean is
a) `text{3 median = mode + 2 mean}`
b) `text{Mode = Mean + Median}`
c) `text{Mode = 3 Median + 3 Mean}`
Answer
1. a.
Q2. Answer in one word/sentence
1. What will be the Arithmetic mean of `1, 2,3,4,5`?
2. What is the mode of `2,4,8,7,5,4,9,6,7,1,7`?
Answer
1. 3, 2. 7.
Ex 14.1
Q1.The following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is Rs. `18.` Find the missing frequency f.
Q2. The table below shows the daily expenditure on food of `25` households in a locality.
Q3. A class teacher has the following absentee record of `40` students of a class for the whole term. Find the mean number of days a student was absent.
Q4. The following table gives the literacy rate (in percentage) of `35` cities. Find the mean literacy rate.
for solution click here (Ex 14.1)
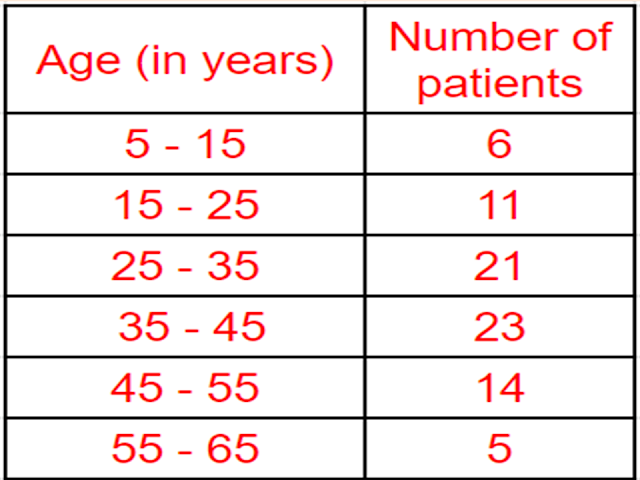
Q1. The following table shows the ages of the patients admitted in a hospital during a year.
Find the mode and the mean of the data given above. Compare and interpret the two measures of central tendency.
for solution click here (Ex 14.2)
Ex 14.3
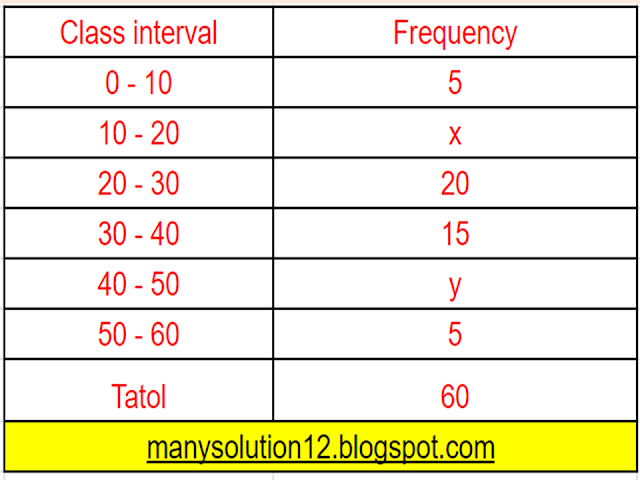
Q1. If the median of the distribution given below is `28.5`, find the value of `x` and `y`.
for solution click here (Ex 14.3)
Chapter 15
Q1. Choose the correct option
1. If `p` is the probability of an event occurring, then the probability that it will not occur will be
a) `1/p` b) `2/p` c) `-p` d) `1-p`
Q2. Which of the following values cannot be the probability of an event?
a) `1/3` b) `0.1` c) `3%` d) `(17)/(16)`
Q3. Which of the following numbers cannot be the probability of an event?
a) `2/3` b) `-1.5` c) `15%` d) `0.7`
Answer
1. d, 2. d, 3. b
Q2. Fill in the blanks.
1. The probability of an impossible event is___.
2. The probability of a certain event is __.
3. The value of the probability is always between __.
Answer
1. 0, 2. 1, 3. 0 and 1
Q3. Write True/False
1. The probability of an event can be greater than `1`.
2. The probability of an event is greater than `1`.
3. The probability of an event cannot be negative.
Answer
1. True, 2. False, 3. True.
Q4.Answer the one-word/sentence.
1. What will be the sum of the probability of an event and the probability of that event not occurring?
2. What is the probability of an impossible?
3. What is the probability of a certain event?
Answer
1. `1`, 2. `0`, 3. `1`
Chapter 15
Q1. Find the probability of getting a head when a coin is tossed once. Also, find the probability of getting a tail.
Q2. A bag contains a red ball, a blue ball, and a yellow ball, all the balls being of the same size. Kritika takes out a ball from the bag without looking into it. What is the probability that she takes out the
i) yellow ball?
ii) red ball?
iii) blue ball?
Q3. Suppose we throw a dice once. i) What is the probability of getting a number greater than 4?
ii) What is the probability of getting a number less than or equal to 4?
Q4. One card is drawn from a well-shuffled deck of 52 cards. Calculate the probability that the card will
i) be an ace,
ii) not be an ace.
Q5. Two players, Sangeeta and Reshma, play a tennis match. It is known that the probability of Sangeeta winning the match is 0.62. What is the probability of Reshma winning the match?
Q6.Savita and Hamida are friends. What is the probability that f. both will have i) different birthdays?
ii) the same birthday?
(ignoring a leap year).
Q7. A box contains 3 blue, and 2 white and 4 red marbles is drawn at random from the box, what is the probability that it will be
i) white?
ii) blue?
iii) red?
Q8. A carton consists of 100 shirts of which 88 are good, 8 have minor defects and 4 have major defects. Jimmy, a trader, will only accept the shirts which are good, but Sujatha, another trader, will only reject the shirts which have major defects. One shirt is drawn at random from the carton. What is the probability that
i) it is acceptable to Jimmy?
ii) it is acceptable to Sujatha?
Q9. If `P(E) = 0.05,` what is the probability of not `E`?
Q10. A bag contains lemon flavoured candies only. Malini takes out one candy without looking into the bag. What is the bag. What is the probability that she takes out
i) an orange flavoured candy?
ii) a lemon flavoured candy?
Q11. It is given that a group of `3` students, the probability of `2` students not having the same birthday is `0.992.` What is the probability that the `2` students have the same birthday?
Q12. A bag contains `3` red balls and `5` black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is (i) red? (ii) not red?
Q13. A box contains `5` red marbles, `8` white marbles, and `4` marbles. One marble is taken out of the box at random. What is the probability that the marble taken out will be (i) red? (ii) white? (iii) not green?
Q14. A die is thrown once. Find the probability of getting
i) a prime number,
ii) a number lying between `2` and `6`,
Q15. i) A lot of `20` bulbs contain `4` defective ones. One bulb is drawn at random from the lot. What is the probability that this bulb is defective?
for solution click here (Ex 15.1)







Comments