10th Maths 7.2
NCERT Class 10th solution of Exercise 7.1
NCERT Class 10th Maths Projects
Exercise 7.2
Q1. Find the coordinates of the point which divides the join of `(-1, 7)` and `(4, -3)` in the ratio `2 : 3`.
Sol. :
Given:
Let `x_1=-1, y_1=7, x_2=4, y_2=3` and `m_1=2, m_2=3`
To find:
The coordinates of the point.
Solve:
Section formula
`x=(m_1x_2+m_2x_1)/(m_1+m_2)`
`x=(2times4+3times(-1))/(2+3)`
`x=(8-3)/5`
`x=5/5`
`x=1`
`y=(m_1y_2+m_2y_1)/(m_1+m_2)`
`y=(2times(-3)+3times7)/(2+3)`
`y=(-6+21)/5`
`y=15/5`
`y=3`
Answer:
The coordinates of the point is `(1, 3)`.
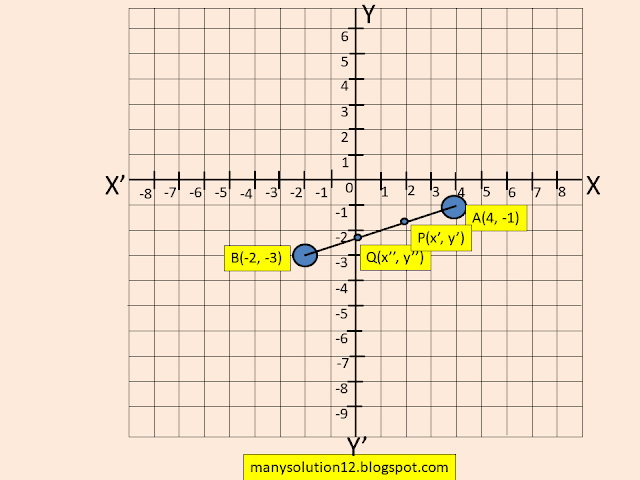
Q2. Find the coordinates of the points of trisection of the line segment joining `(4, -1)` and `(-2, -3)`.
Sol. :
Let `x_1=4, y_1=-1, x_2=-2, y_2=-3`.
To Find:
The coordinates of the points.
Solve:
For `P`
`m_1=1, m_2=2`
`x'=(m_1x_2+m_2x_1)/(m_1+m_2)`
`x'=(1times(-2)+2times4)/(1+2)`
`x'=(-2+8)/3`
`x'=6/3`
`x'=2`
`y'=(m_1y_2+m_2y_1)/(m_1+m_2)`
`y'=(1times(-3)+2times(-1))/(1+2)`
`y'=(-3-2)/3`
`y=-5/3`
For `Q`
`m_1=2, m_2=1`
`x''=(m_1x_2+m_2x_1)/(m_1+m_2)`
`x''=(2times(-2)+1times4)/(2+1)`
`x''=(-4+4)/3`
`x''=0/3`
`x''=0`
`y''=(m_1y_2+m_2y_1)/(m_1+m_2)`
`y''=(2times(-3)+1times(-1))/(2+1)`
`y''=(-6-1)/3`
`y''=-7/3`
Answer:
The coordinates of the points are `(2, -5/3)` and `(0, -7/3)`.
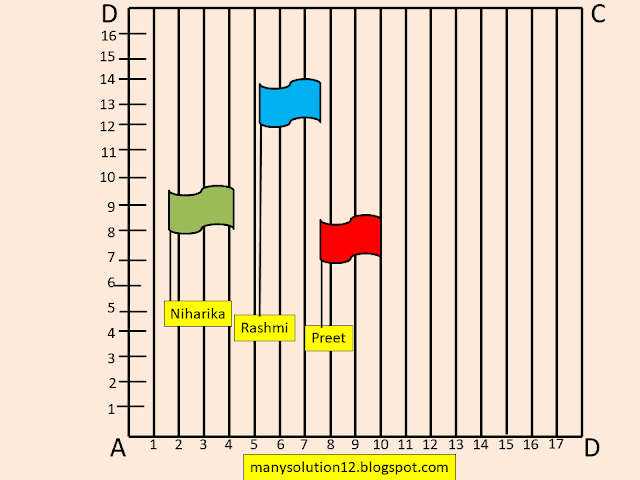
Q3. To conduct Sports Day activities, in your rectangular shaped school ground `ABCD`, lines have been drawn with chalk powder at a distance of `1 m` each. `100` flower pots have been placed at a distance of `1 m` from each other along `AD`, as shown in figure. Niharika runs `1/4` th the distance `AD` on the `2nd` line and posts a green flag. Preet runs `1/5`th the distance `AD` on the eight line and post a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?
Sol. :
Let `(2, 100/4)=(2, 25), (8, 100/5)=(8, 20), (x, y)`
To Find:
The distance between both flags, and the distance of the blue flag post.
Solve:
`=sqrt((8-2)^2+(20-25)^2)`
`=sqrt((6)^2+(-5)^2)`
`=sqrt(36+25)`
`=sqrt(61)m`
`x=(8+2)/2=10/2=5m`
`y=(20+25)/2=45/2=22.5m`
Answer:
The distance between both flags is `sqrt(61)m` and the distance of the blue flag post is `22,5m`.
Q4. Find the ratio in which the line segment joining the points `(-3, 10)` and `(6, -8)` is divided by `(-1, 6)`.
Sol. :
Given:
Let `x=-1,y=6` and `x_1=-3, y_1=10, x_2=6, y_2=-8`
To Find :
`m_1` and `m_2`
Solve:
`x=(m_1x_2+m_2x_1)/(m_1+m_2)`
`-1=(m_2times6+m_2times(-3))/(m_1+m_2)`
`-1=(6m_1-3m_2)/(m_1+m_2)`
`-m_1-m_2=6m_1-3m_2`
`6m_1+m_1=3m_2-m_2`
`7m_1=2m_2`
`m_1/m_2=2/7`
`m_1:m_2=2:7`
Answer:
The `m_1=2, m_2=7`.
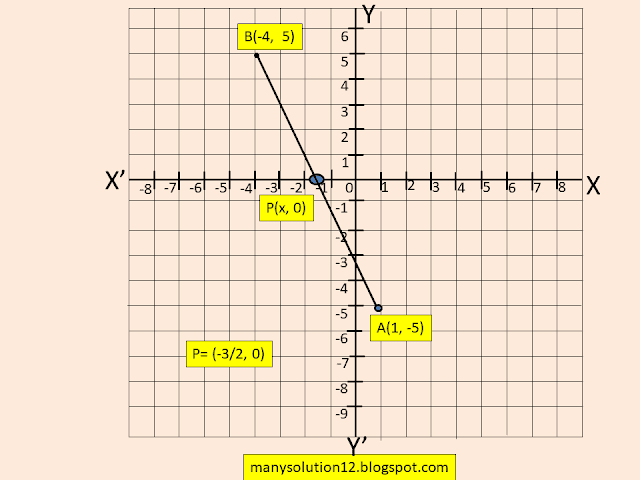
Q5. Find the ratio in which the line segment joining `A(1,-5)` and `B(-4, 5)` is divided by the `x-`axis. Also find the coordinates of the point of division.
Sol. :
Given:
Let `P(x, 0)` of `x`-axis, `A(1, -5), B(-4, 5)`
To Find:
The ratio and the coordinates of the point of division.
Solve:
`y=(m_1y_2+m_2y_1)/(m_1+m_2)`
`0=(m_1times5+m_2times(-5))/(m_1+m_2)`
`0=5m_1-5m_2`
`m_1=m_2`
`m_1:m_2=1:1`
`P` is mid-point of `AB`
`x=(x_1+x_2)/(1+1)=(1-4)/2=-3/2`
`P(-3/2, 0)`
Answer:
The ratio is `1:1` and the coordinates of the point of division `(-3/2, 0)`.
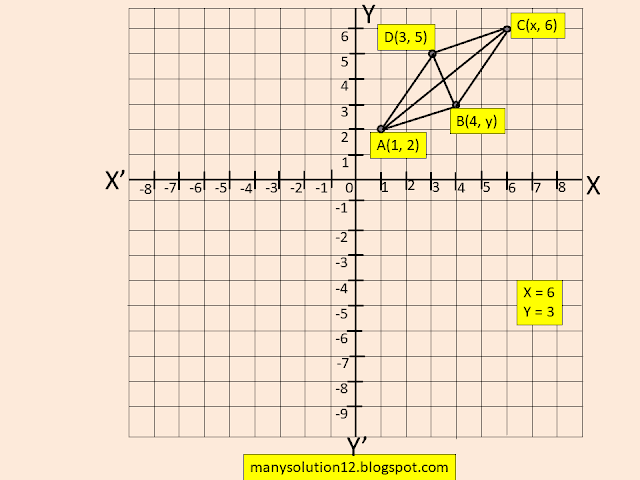
Q6. If `(1,2), (4, y), (x, 6)` and `(3, 5)` are the vertices of a parallelogram taken in order, find `x` and `y`.
Sol. :
Let the vertices of parallelogram `A(1, 2), B(4, y), C(x, 6)` and `(3, 5)`
To Find:
The value of `x` and `y`.
Solve:
The diagonals `AC` and `BD` of the parallelogram bisect each other at `O(x', y')`
midpoint of `AC` = midpoint of `BD`
`((1+x)/2, (2+6)/2)=((4+3)/2, (y+5)/2)`
`((1+x)/2, 8/2)=(7/2, (y+5)/2)`
`((1+x)/2, 4)=(7/2, (y+5)/2)`
`(1+x)/2=7/2`
`1+x=7`
`x=7-1`
`x=6`
and
`(y+5)/2=4`
`y+5=8`
`y=8-5`
`y=3`
Answer:
The value of `x=6` and `y=3`.
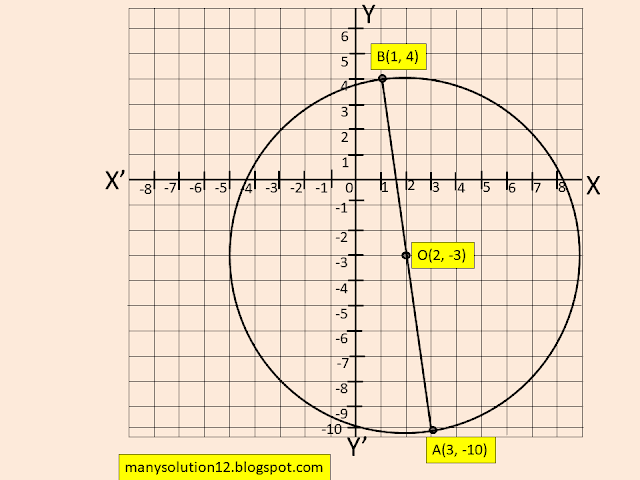
Q7. Find the coordinates of a point `A`, where `AB` is the diameter of a circle whose centre is `(2, -3)` and `B` is `(1, 4)`.
Sol. :
The Centre of the circle is `O(2, -3)` and point `B(1, 4)`.
To Find:
The coordinates of a point `A`.
Solve:
The centre `O` of the circle is the midpoint of the diameter `AB`.
`O=(A+B)/2`
`(2, 3)=((x+1)/2, (y+4)/2)`
`2=(x+1)/2`
`4=x+1`
`x=3`
and
`y=(y+4)/2`
`2y=y+4`
`2y-y=4`
`y=4`
Answer:
The coordinates of a point `A(3, 4)`.
Q8. If `A` and `B` are `(-2, -2)` and `(2, -4)`, respectively, find the coordinates of `P` such that `AP=3/7AB` and `P` lies on the line segment `AB`.
Sol:
Given:
`A(-2, -2), B(2, -4)` and `AP=3/7AB`
To Find:
The coordinates of `P`.
Solve:
`BP=AB-AP`
`BP=AB-3/7AB` [`AP=3/7AB`]
`BP=(7AB-3AB)/7`
`BP=4/7AB`
Point `P` divides the segment `AB` in `3:4`.
`P(x, y)=((m_1x_2+m_2x_1)/(m_1+m_2), (m_1y_2+m_2y_1)/(m_1+m_2))`
`x=(3times2+4times(-2))/(3+4)=(6-8)/7=-2/7`
`y=(3times(-4)+4times(-2))/(3+4)=(-12-8)/7=-20/7`
Answer:
The coordinates of `P(-2/7, -20/7)`.
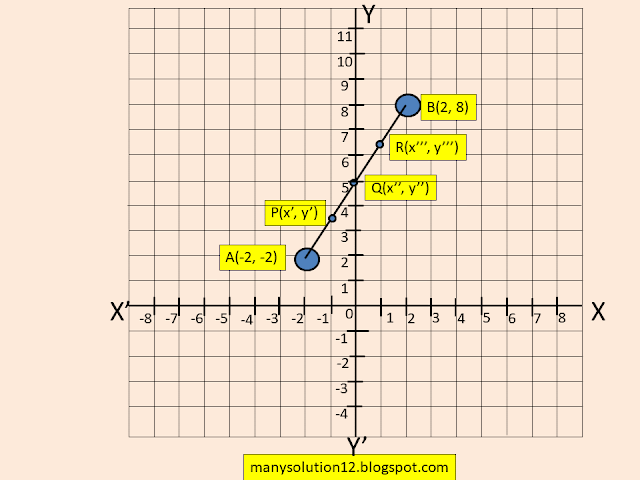
Q9. Find the coordinates of the points which divide the line segment joining `A(-2, 2)` and `B(2, 8)` into four equal parts.
Sol. :
`A(-2, 2), B(2, 8)`
To Find:
The coordinates of the points divide `AB` into four equal points.
Solve:
`Q` is the midpoint of `AB`
`Q(x'', y'')=((-2+2)/2, (2+8)/2)=(0, 5)`
`P` is the midpoint of `AQ`
`P(x', y')=((-2+0)/2, (2+5)/2)=(-1, 7/2)`
`R` is the midpoint of `QB`
`R(x''', y''')=((0+2)/2, (5+8)/2)=(1, 13/2)`
Answer:
The coordinates of the points divide `AB` into four equal points are `Q(0, 5), P(-1, 7/2), R(1, 13/2)`.
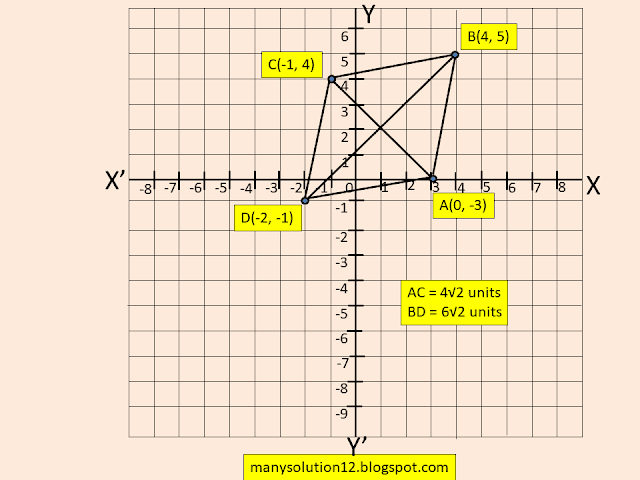
Q10. Find the area of a rhombus if its vertices are `(3, 0), (4, 5), (-1, 4)` and `(-2, -1)` takes in order. [Hint: Area of a rhombus`=1/2`(product of its diagonals)]
Sol. :
Given:
Let vertices of rhombus are `A(3,0), B(4, 5), C(-1, 4)` and `D(-2, -1)`.
To Find:
Area of a rhombus.
Solve:
Diagonal `AC`
`AC=sqrt((-1-3)^2+(4-0)^2)`
`AC=sqrt((-4)^2+(4)^2)`
`AC=sqrt(16+16)=4sqrt2`
Diagonal `BD`
`BD=sqrt((-2-4)^2+(-1-5)^2)`
`BD=sqrt((-6)^2+(-6)^2`
`BD=sqrt(36+36)`
`BD=6sqrt2`
Area of a rhombus`=1/2(ACtimesBD)`
`=1/2(4sqrt2times6sqrt2)`
`=24` square units
Answer:
The area of a rhombus `24` square units.



Comments