10th Maths 7.3
NCERT Class 10th solution of Exercise 7.1
Exercise 7.3
Q1. Find the area of the triangle whose vertices are:
i) `(2, 3), (-1, 0), (2, -4)`
ii) `(-5, -1), (3, -5), (5, 2)`
Sol. :
i)
Given:
Let `A(2, 3), B(-1, 0),` and `C(2, -4)`
Solve:
Area of `triangle=1/2[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
`ar(ABC)=1/2[2(0+4)+(-1)(-4-3)+2(3-0)]`
`ar(ABC)=1/2[2(4)+(-1)(-7)+2(3)]`
`ar(ABC)=1/2[8+7+6]`
`ar(ABC)=21/2` square units
Answer:
The area of `triangleABC` is `21/2` square units.
ii)
Given:
Let `A(-5, -1), B(3, -5),` and `C(5, 2)`
Solve:
Area of `triangle=1/2[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
`ar(ABC)=1/2[-5(-5-2)+3(2+1)+5(-1+5)]`
`ar(ABC)=1/2[-5(-7)+3(3)+5(4)]`
`ar(ABC)=1/2[35+9+20]`
`ar(ABC)=1/2[64]`
`ar(ABC)=32` square units
Answer:
The area of `triangleABC` is `32` square units.
Q2. In each of the following find the value of `k`, for which the points are collinear.
i) `(7, -2), (5, 1), (3, k)`
ii) `(8, 1), (k, -4), (2, -5)`
Sol. :
i)
Given:
Let `A(7, -2), B(5, 1),` and `C(3, k)` are collinear.
Solve:
We know that
The points `A, B,` and `C` are collinear, then `ar(ABC)=0`.
Area of `triangle=1/2[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
`ar(ABC)=1/2[7(1-k)+5(k+2)+3(-2-1)]`
`0=1/2[7-7k+5k+10+3(-3)]`
`0=1/2[17-2k-9]`
`0=1/2[8-2k]`
`0=8-2k`
`2k=8`
`k=8/2`
`k=4`
Answer:
The value of `k=4`.
ii)
Given:
Let `A(8, 1), B(k, -4),` and `C(2, -5)` are collinear.
Solve:
We know that
The points `A, B,` and `C` are collinear then `ar(ABC)=0`.
Area of `triangle=1/2[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
`ar(ABC)=1/2[8(-4+5)+k(-5-1)+2(1+4)]`
`0=1/2[8(1)+k(-6)+2(5)]`
`0=1/2[8-6k+10]`
`0=1/2[18-6k]`
`k=18/6`
`k=3
Answer:
The value of `k=3`.
Q3. Find the area of the triangle formed by joining the mid-points to the sides of the triangle whose vertices are `(0, -1), (2,1)` and `(0, 3)`. Find the ratio of this area to the area of the given triangle.
Sol. :
Let `A(0, -1), (2, 1),` and `C(0, 3)`
To Find:
The ratio of the formed `triangle` area of the given `triangle`.
Solve:
The midpoint of `AB` is `P`
`P=((0+2)/2, (-1+1)/2)=(1, 0)`
The midpoint of `BC` is `Q`
`Q=((2+0)/2, (1+3)/2)=(1, 2)`
The midpoint of `CA` is `R`
`R=((0+0)/2, (3-1)/2)=(0, 1)`
Area of `triangle=1/2[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
`ar(ABC)=1/2[0(1-3)+2(3+1)+0(-1-1)]`
`ar(ABC)=1/2[0+2(4)+0]`
`ar(ABC)=1/2times8=4` square units
And
`ar(PQR)=1/2[1(2-1)+1(1-0)+0(0-2)]`
`ar(PQR)=1/2[1+1-0]`
`ar(PQR)=1/2times2=1` square units
The ratio of `ar(ABC)` and `ar(PQR)`
`(ar(ABC))/(ar(PQR))=1/4`
`ar(ABC) : ar(PQR)=1:4`
Answer:
The ratio of the formed `triangle` area to the given `triangle` is `1:4`.
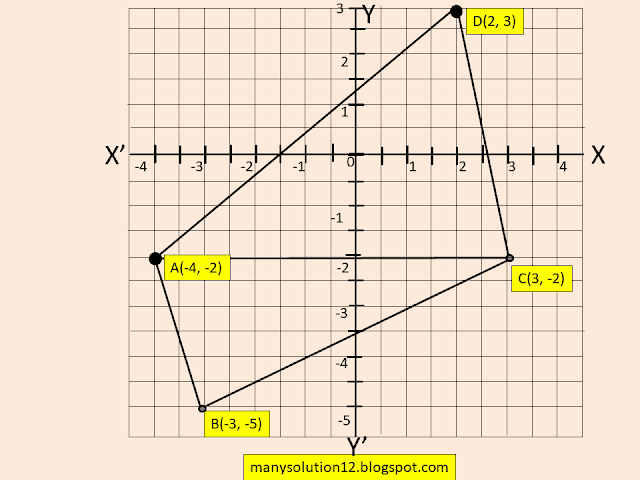
Q4. Find the area of the quadrilateral whose vertices, takes in order, are `(-4, -2), (-3, -5), (3, -2)` and `(2, 3)`.
Sol. :
Let the vertices of parallelogram `A(-4, -2), B(-3, -5), C(3, -2)` and `D(2, 3)`
Construction:
Join `AC`
To Find:
The area of the parallelogram `ABCD`.
Solve:
Area of `triangle=1/2[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
`ar(ABC)=1/2[-4(-5+2)+(-3)(-2+2)+3(-2+5)]`
`ar(ABC)=1/2[-4(-3)+(-3)(0)+3(3)]`
`ar(ABC)=1/2[12-0+9]`
`ar(ABC)=1/2times21=21/2` square units
and
`ar(ACD)=1/2[-4(-2-3)+3(3+2)+2(-2+2)]`
`ar(ACD)=1/2[-4(-5)+3(5)+2(0)]`
`ar(ACD)=1/2[20+15+0]`
`ar(ACD)=1/2[35]=35/2` square units
`ar(ABCD)=ar(ABC)+ar(ACD)`
`ar(ABCD)=21/2+35/2=56/2=28` square units.
Answer:
The area of parallelogram `ABCD=28` square units.
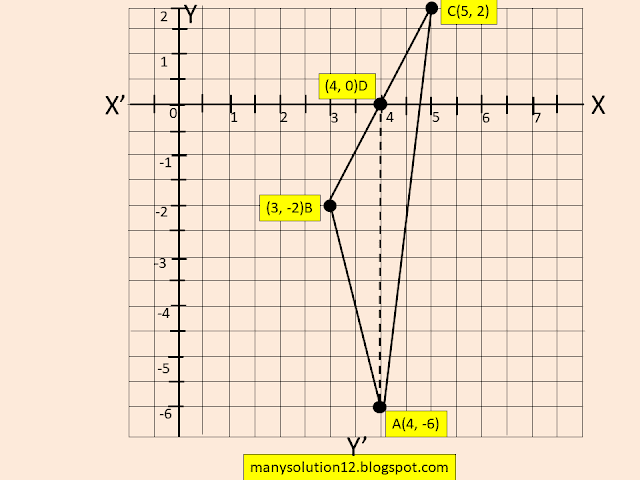
Q5. You have studied in Class IX, (Chapter 9, Example 3), that a median of a triangle divides it into two triangles of equal area. Verify this result for `triangle ABC` whose vertices are `A(4, -6), B(3, -2)` and `C(5, 2).`
Sol. :
`A(4, -6), B(3, -2)` and `C(5, 2)`
To Verify:
A median of a `triangle` divides it into two `triangle`s of equal areas.
Solve:
In `triangle ABC` `AD` is median that bisect `BC` at `D`
Let `D(x, y)`
`x=(3+5)/2=4,`
`y= (-2+2)/2=0`
In `triangle ADB`
`A(4, 6), D(4, 0), B(3, -2)`
Area of `triangle=1/2[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
`ar(ADB)=1/2[4(0+2)+4(-2+6)+3(-6-0)]`
`ar(ADB)=1/2[8+16-18]`
`ar(ADB)=1/2times6=3` square units
and
In `triangle ADC`
`A(4, 6), B(4, 0), C(5, 2)`
`ar(ADC)=1/2[4(0-2)+4(2+6)+5(-6-0)]`
`ar(ADC)=1/2(-8+32-30)`
`ar(ADC)=1/2times(-6)=-3` square units.
Since area is a measure, which cannot be negative.
`ar(ADC)=3` square units
`ar(ADB)=ar(ADC)`
A median of the `triangle` divides it into two `triangle`s of equal areas.
Verified.




Comments