10th Maths 3.2
NCERT Class 10th solution of Exercise 3.1
NCERT Class 10th solution of Exercise 3.5
NCERT Class 10th solution of Exercise 3.6
Exercise 3.2
Q1. From the pair of linear equations in the following problems, and find their solutions graphically.
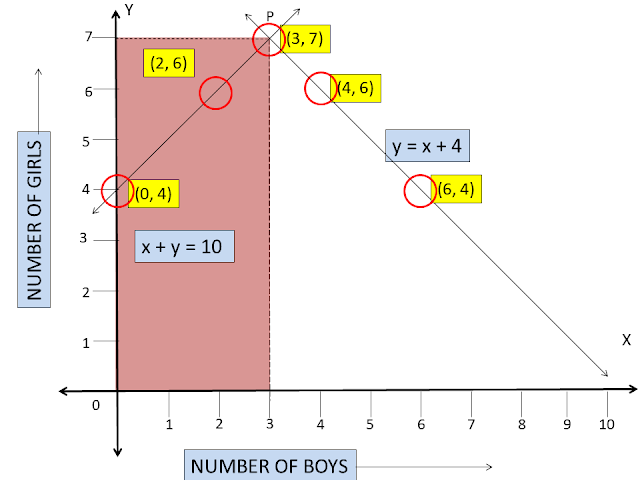
i) `10` students of Class `X` took part in a Mathematics quiz. If the number of girls is `4` more than the number of boys, find the number of boys and girls who took part in the quiz.
ii) `5` pencils and `7` pens together cost `₹50`, whereas `7` pencils and `5` pens together cost `₹46`. Find the cost of one pencil and that one pen.
Sol. :
i)
Let the number of boys in Mathematical qize are `x`,
and the number of girls in Mathematical qize are `y`
According to question
`x+y=10`______(1)
and
`y=x+4`_______(2)
from equation (1)
when `x=4`
`4+y=10`
`y=10-4`
`y=6`
when `x=6`
`6+y=10`
`y=10-6`
`y=4`
from equation (2)
when `x=0`
`y=0+4`
`y=4`
when `x=2`
`y=2+4`
`y=6`
X | 4 | 6 |
y | 6 | 4 |
X | 4 | 2 |
y | 6 | 6 |
Thus, the number of Girls `7` and the number of boys `3`.
ii)
Let the cost of one pencil `₹x`,
and
Let the cost of one pen`₹y`.
According to question
`5x+7y=50`_______(1)
`7x+5y=46`_______(2)
from equation (1)
when `x=3`
`5(3)+7y=50`
`15+7y=50`
`7y=50-15`
`7y=35`
`y=35/7`
`y=5`
when `x=-4`
`5(-4)+7y=50`
`-20+7y=50`
`7y=50+20`
`7y=70`
`y=70/7`
`y=10`
from equation (2)
when `x=3`
`7(3)+5y=46`
`21+5y=46`
`5y=46-21`
`5y=25`
`y=25/5`
`y=5`
when `x=-2`
`7(-2)+5y=46`
`-14+5y=46`
`5y=46+14`
`5y=60`
`y=60/5`
`y=12`
|
X |
3 |
-4 |
|
y |
5 |
6 |
|
X |
3 |
-2 |
|
y |
5 |
12 |
Thus, the cost of one pencil `₹3` and cost of one pen are `₹5`.
Q2. On comparing the ratios `a_1/a_2, b_1/b_2, and c_1/c_2`, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident :
i)
`5x-4y+8=0`
`7x+6y-9=0`
ii)
`9x+3y+12=0`
`18x+6y+24=0`
iii)
`6x-3y+10=0`
`2x-y+9=0`
Sol. :
i)
`5x-4y+8=0`__________(1)
`7x+6y-9=0`__________(2)
`a_1/a_2=5/7, b_1/b_2=(-4)/6=(-2)/3, c_1/c_2=8/-9`
`a_1/a_2 ne b_1/b_2 ne c_1/c_2`
Answer :
Intersect at a point.
ii)
`9x+3y+12=0`________(1)
`18x+6y+24=0`_______(2)
`a_1/a_2=9/18=1/2. b_1/b_2=3/6=1/2, c_1/c_2=12/24=1/2`
`a_1/a_2=b_1/b_2=c_1/c_2`
Answer:
Coincident.
iii)
`6x-3y+10=0`_______(1)
`2x-y+9=0`_________(2)
`a_1/a_2=6/2=3/1, b_1/b_2=(-3)/1, c_1/c_2=10/9`
`a_1/a_2 = b_1/b_2 ne c_1/c_2`
Answer:
Parallel.
Q3. On comparing the ratios `a_1/a_2, b_1/b_2, and c_1/c_2`, find out whether the following pair of linear equations are consistent, or inconsistent.
i) `3x+2y=5; 2x-3y=7`
ii) `2x-3y=8; 4x-6y=9`
iii) `35/23x+(-y)=7; 9x-10y=14`
iv) `5x-3y=11; -10x+6y=-22`
v) `4/3x+2y=8; 2x+3y=12`
Sol. :
i)
`3x+2y=5`
`3x+2y-5=0`_______(1)
`2x-3y=7`
`2x-3y-7=0`________(2)
`a_1/q_2=3/2, b_1/b_2=2/-3, c_1/c_2=(-5)/-7=5/7`
`a_1/a_2 ne b_1/b_2 ne c_1/c_2`
Answer :
Consistent.
ii)
`2x-3y=8`
`2x-3y-8=0`_________(1)
`4x-6y=9`
`4x-6y-9=0`_________(2)
`a_1/a_2=2/4=1/2, b_1/b_2=(-3)/-6=1/2, c_1/c_2=(-8)/-9=8/9`
`a_1/a_2 =b_1/b_2 ne c_1/c_2`
Answer :
Inconsistent.
iii)
`3/5x+5/3y=7`
`9x+25y-42=0`_______(1)
`9x-10y=14`
`9x-10y-14=0`________(2)
`a_1/a_2=9/9=1, b_1/b_2=10/(-10)=-1, c_1/c_2=(-42)/-14`
`a_1/a_2 ne b_1/b_2 ne c_1/c_2`
Answer :
Consistent.
iv)
`5x-3y=11`
`5x-3y-11=0`________(1)
`-10x+6y=-22`
`-10x+6y+22=0`______(2)
`a_1/a_2=5/-10=1/-2, b_1/b_2=(-3)/6=(-1)/2, c_1/c_2=(-24)/-12=2`
`a_1/a_2= b_1/b_2= c_1/c_2`
Answer :
Consistnet.
v)
`4/3x+2y=8`
`4x+6y-24=0`_______(1)
`2x+3y=12`
`2x+3y-12=0`_______(2)
`a_1/a_2=4/2=2/1, b_1/b_2=6/3=2/1, c_1/c_2=(-24)/-12=2/1`
`a_1/a_2 = b_1/b_2 = c_1/c_2`
Answer :
Consistent
Q4. Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain in the solution graphically:
i) `x+y=5, 2x+2y=10`
ii) `x-y=8, 3x-3y=16`
iii) `2x+y-6=0, 4x-2y-4=0`
iv) `2x-2y-2=0, 4x-4y-5=0`
Sol. :
i)
`x+y=5`
`x+y-5=0`________(1)
`2x+2y=10`
`2x+2y-10=0`______(2)
`a_1/a_2=1/2, b_1/b_2=1/2, c_1/c_2=1/2`
`a_1/a_2, b_1/b_2, c_1/c_2`
Thus, the pair of equations is consistent.
Graphical solution
from equation (1)
when `x=0`
`0+y=5`
`y=5`
when `x=5`
`5+y=5`
`y=5-5`
`y=0`
from equation
when `x=0`
`2(0)+2y=10`
`0+2y=10`
`y=10/2`
`y=5`
when `x=5`
`2(5)+2y=10`
`10+2y=10`
`2y=10-10`
`y=0/2`
`y=0`
X | 0 | 5 |
y | 5 | 0 |
X | 0 | 5 |
y | 5 | 0 |
Answer :
Thus, there are infinitely many solutions of the given pair of linear equations.
ii)
`x-y=8`
`x-y-8=0`________(1)
`3x-3y=16`
`3x-3y-16=0______(2)
`a_1/a_2=1/3, b_1/b_2=-1/-3, c_1/c_2=-8/-16=3/2`
`a_1/a_2 = b_1/b_2 ne c_1/c_2`
Answer:
Thus, the given pair of linear equations is consistent.
iii)
`2x+y-6=0`_________(1)
`4x-2y-4=0`_________(2)
`a_1/a_2=2/4=1/2, b_1/b_2=1/-2, c_1/c_2=-6/-4=3/2`
`a_1/a_2 ne b_1/b_2 ne c_1/c_2`
Thus, the given pair of linear equations is consistent.
Graphical solution
from equation (1)
when `x=0`
`2(0)+y-6=0`
`0+y-6=0`
`y=6`
when `x=3`
`2(3)+y-6=0`
`6+y-6=0`
`y=0`
from equation (2)
when `x=1`
`4(1)-2y-4=0`
`4-2y-4=0`
`0-2y=0`
`y=0`
when `x=4`
`4(4)-2y-4=0`
`16-2y-4=0`
`2y=12`
`y=6`
X | 0 | 3 |
y | 6 | 0 |
X | 1 | 4 |
y | 0 | 6 |
Answer :
Thus, the required solution of the given pair of linear equations is `x=2`and `y=2`
iv)
`2x-2y-2=0`_______(1)
`4x-4y-5=0`_______(2)
`a_1/a_2=2/4=1/2, b_1/b_2=-2/-4=1/2, c_1/c_2=-2/-5=2/5`
`a_1/a_2= b_1/b_2 ne c_1/c_2`
Answer:
Thus, the given pair of linear equations is inconsistent.
Q5. Half the perimeter of a rectangular garden, whose length is `4 m` more than its width, is `36 m`. Find the dimensions of the garden.
Sol. :
Let the length of the rectangle is `x m`,
and the width of the rectangle is `ym.`
According to question
`x=y+4`_________(1)
`x+y=36`________(2)
from equation (1)
when `x=16`
`16=y+4`
`y=16-4`
`y=12`
when `x=12`
`12=y+4`
`y=12-4`
`y=8`
from equation (2)
when `x=16`
`16+y=36`
`y=36-16`
`y=20`
when `x=24`
`24+y=36`
`y=36-24`
`y=12`
X | 16 | 12 |
y | 12 | 8 |
X | 16 | 24 |
y | 20 | 12 |
The required dimensions of the garden are `20 m` and `16 m`.
Q6. Given the linear equation `2x+3y-8=0`, write another linear equation in two variables such that the geometrical representation of the pair so formed is:
i) intersecting lines ii) parallel lines iii) coincident lines.
Sol. :
One possible answer for the three-part
i) `3x+2y-7=0`
ii) `2x+3y-12=0`
iii) `4x+6y-16=0`
Note:
There can be several answers.
Q7. Draw the graphs of the equations `x-y+1=0` and `3x+2y-12=0`. Determine the coordinates of the vertices of the triangle formed by these lines and the `x`-axis, and shad the triangular region.
Sol. :
`x-y+1=0`__________(1)
`3x+2y-12=0`_______(2)
from equation (1)
when `x=0`
`0-y+1=0`
`-y=-1`
`y=1`
when `x=5`
`5-y-1=0`
`-y+4=0`
`-y=-4`
`y=4`
from equation (2)
when `x=0`
`3(0)+2y-12=0`
`0+2y-12=0`
`2y=12`
`y=12/2`
`y=6`
when `x=4`
`3(4)+2y-12=0`
`12+2y-12=0`
`2y+0=0`
`2y=0`
`y=0/2`
`y=0`
X | 0 | 5 |
y | 1 | 6 |
X | 0 | 4 |
y | 6 | 0 |
Answer :
Vertices of the triangle are `A (2, 3), B(-1, 0) and C(4, 0)`.








Comments