10th Maths 13.3
NCERT Class 10th solution of Exercise 13.1
NCERT Class 10th solution of Exercise 13.2
Exercise 13.3
Take `pi = 22/7` unless stated otherwise.
Q1. A metallic sphere of radius `text{4.2 cm}` is melted and recast into the shape of a cylinder of radius `text{6 cm}`. Find the height of the cylinder.
`text{Sol. :}`
`text{Given :}`
`text{Radius of Sphere }R = 4.2 text{ cm}`
`text{Radius of Cylinder }r = 6 text{ cm}`
`text{To find :}`
`text{Height of the Cylinder}`
`text{Solve :}`
`text{According to question}`
`text{Volume of the Cylinder = Volume of the Sphere}`
`pir^2h = 4/3piR^3`
`h = (4piR^3)/(3pir^2)`
`h = (4R^3)/(3r^2)`
`h = (4times(4.2)^3)/(3(6)^2)`
`h = (4times4.2times4.2times4.2)/(3times6times6)`
`h = (4times4.2times0.7times0.7)/3`
`h = (8.232)/3`
`h = 2.744text{ cm}`
`text{Answer :}`
`text{The height of the cylinder 2.744 cm.`
☝
Like, Share, and Subscribe.
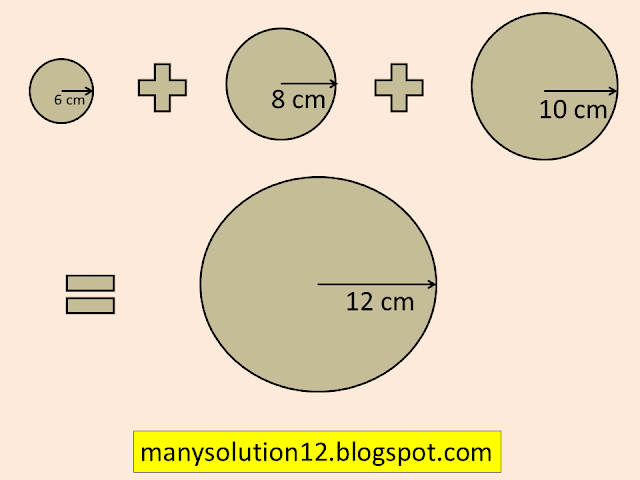
Q2. Metallic spheres of radii `text{6 cm, 8 cm}` and `text{10 cm,}` respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
`text{Sol. :}`
`text{Given :}`
`text{Radius of metal sphere }r_1 = 6, r_2 = 8, r_3 = 10 text{cm}`
`text{To find :}`
`text{The radius of the resulting sphere}`
`text{Solve :}`
`text{Let Radius of resulting sphere = R}`
`text{According to question}`
`text{Vol. of result Sphere = Sum of Vol. of 3 Spheres}`
`4/3piR^3 = 4/3pir_1^3 + 4/3pir_2^2 + 4/3pir_3^3`
`4/3piR^3 = 4/3pi(r_1^3 + r_2^3 + r_3^3)`
`R^3 = (r_1^3 + r_2^3 + r_3^3)`
`R^3 = ((6)^3 + (8)^3 + (10)^3)`
`R^3 = (216 + 512 + 1000)`
`R^3 = 1728`
`R^3 = (12)^3`
`R = 12 text{ cm}`
`text{Answer :}`
`text{The radius of resulting sphere 12 cm}.`
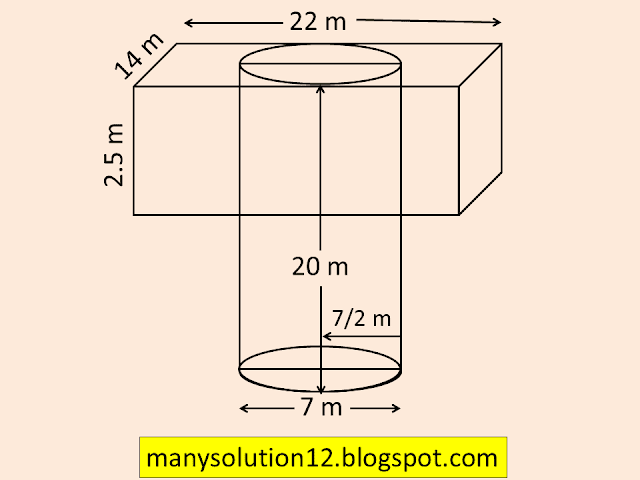
Q3. A `text{20 m}` deep well with diameter `text{7 m}` is dug and the earth from digging is evenly spread out to form a platform `text{22 m}` by `text{14 m}`. Find the height of the platform.
`text{Sol. :}`
`text{Given :}`
`text{Depth (height) of the well (cylinder) } h = 20 text{cm}`
`text{Diameter of the well (cylinder) }d = 7text{ cm}`
`text{Radius of the well (cylinder) } r = 7/2text{ cm}`
`text{To find :}`
`text{The height of the platform}`
`text{Solve :}`
`text{According to question}`
`text{Vol. of platform(cuboid) = Vol. of well(cylinder)}`
`LtimesBtimesH = pir^2h`
`22times14timesh = 22/7times(7/2)^2times20`
`h = (22times49times20)/(7times4times22times14)`
`h = 5/2`
`h = 2.5 text{ m}`
`text{Answer :}`
`text{The height of the platform is 2.5 m}.`
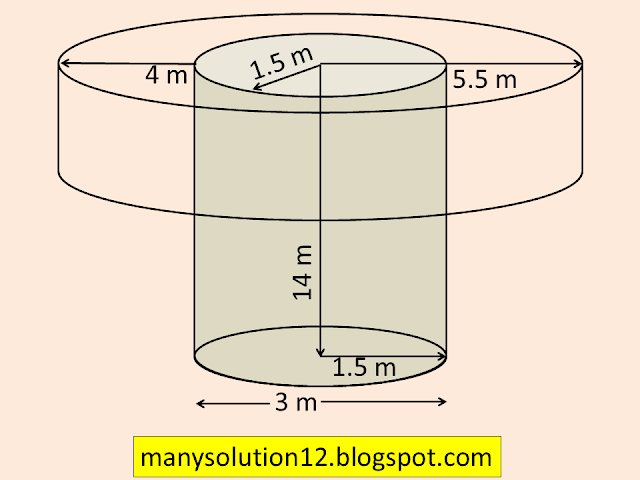
Q4. A well of diameter `text{3 m}` is dug `text{14 m}` deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width `text{4 m}` to form an embankment. Find the height of the embankment.
`text{Sol. :}`
`text{Given :}`
`text{Diameter of well (cylinder) }d = 3text{ m}`
`text{Radius of well (cylinder) }r_1 = 3/2 = 1.5 text{ m}`
`text{Depth (height) of well (cylinder) }h = 14text{ m}`
`text{Width of embankment} = 4text{m }`
`text{Radius of big circle }r_2 = 4 + 1.5 = 5.5text{ m}`
`text{To find :}`
`text{The height of the embankment.}`
`text{Solve :}`
`text{height of the embankment} = x`
`text{According to question}`
`text{Volume of embankment = Volume of well}`
`pi(r_2^2 - r_1^2)x = pir_1^2h`
`[(5.5)^2 - (1.5)^2]x = (1.5)^2times14`
`[(5.5+1.5)(5.5 - 1.5)]x = 2.25times14`
`[7times4]x = 2.25times14`
`x = (2.25times14)/(7times4)`
`x = 1.125 text{ m}`
`text{Answer :}`
`text{The height of the embankment 1.125 m.}`
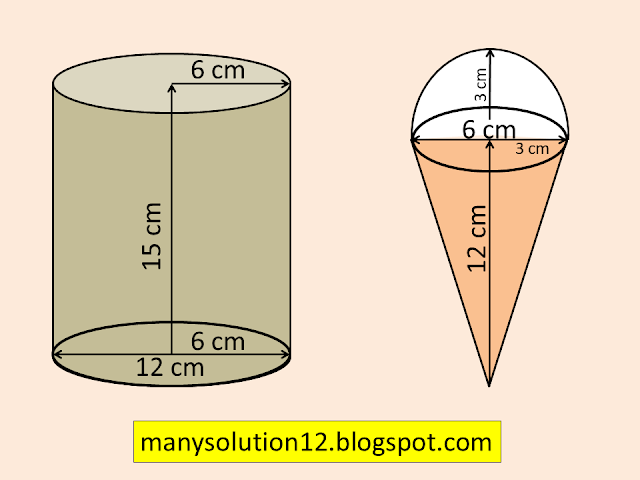
Q5. A container shaped like a right circular cylinder having diameter `text{12 cm}` and height `text{15 cm}` is full of ice cream. The ice cream is to be filled into cones of height `text{12 cm}` and diameter `text{6 cm},` having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
`text{Sol. :}`
`text{Given :}`
`text{Diameter of Cylinder }d = 12text{ cm}`
`text{Radius of Cylinder }r = 6text{ cm}`
`text{Height of Cylinder }h =15text{ cm}`
`text{Hight of Cone }h' = 12text{ cm}`
`text{Diameter of Cone }d' = 6text{ cm}`
`text{Radius of Cone & hemisphere }r' = 3text{ cm}`
`text{To find :}`
`text{The of ice-cream cones.}`
`text{Solve :}`
`text{According to question}`
`text{Volume of ice-cream Cylinder}= pir^2h`
`text{V}_1 = pi(6)^(2)15`
`text{V}_1 = 540pi`
`text{Vol. of ice-cream cone = Vol. of cone}`
`text{ + Vol. of hemisphere}`
`text{V}_2 = 1/3pi(r')^2h' + 2/3pi(r')^3`
`text{ } = (pi(r')^2)/3(h' + 2r')`
`text{ } = (pi(3)^2)/3(12+2times3)`
`text{ } = 3times18pi`
`text{ } = 54pi`
`text{ Number of ice-cream cones }= V_1/V_2`
`text{ Number of ice-cream cones }= (540pi)/(54pi)`
`text{ = }10`
`text{Answer :}`
`text{The number of ice-cream cones 10.}`
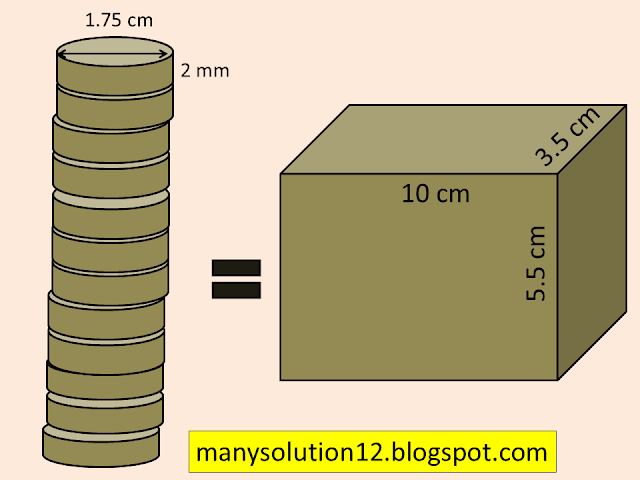
Q6. How many silver coins, `text{1.75 cm}` in diameter and of thickness `text{2 mm}`, must be melted to form a cuboid of dimensions `text{5.5 cm}times text{10 cm} times text{3.5 cm}`?
`text{Sol. :}`
`text{Given :}`
`text{Dimensions of cuboid are }5.5 times 10 times 3.5text{ cm}`
`text{Thickness (height) of coin }h = 2 text{ mm} = 0.2text{ cm}`
`text{Diameter of coin }d = 1.75text{ cm}`
`text{Radius of coin }r = 1.75/2text{ cm}`
`text{To find :}`
`text{Number of coins}`
`text{Solve :}`
`text{Vol. of Cuboid =}Ltimes B times H`
`text{V}_1 = 5.5times10times3.5`
`text{ } = 192.5text{cm}^3`
`text{Vol. of Coin (cylinder) } = pir^2h`
`text{V}_2 = 22/7times(1.75/2)^2times0.2`
`text{ } = 13.475/28`
`text{Number of coins }= V_1/V_2`
`text{ }= (192.5times28)/13.475`
`text{ }= 5390/13.475`
`text{ }= 5390000/13475`
`text{ }= 400`
`text{Answer :}`
`text{The number of coins 400}.`
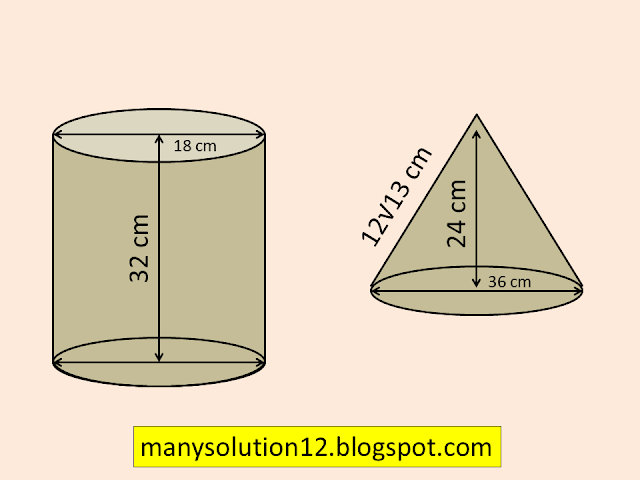
Q7. A cylindrical bucket, `text{32 cm}` height and with radius of base `text{18 cm,}` is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is `text{24 cm,}` find the radius and slant height of the heap.
`text{Sol. :}`
`text{Given :}`
`text{Height of cylindrical bucket }h = 32text{ cm}`
`text{Radius of cylindrical bucket }r = 18text{cm}`
`text{Height of conical heap}h_1 = 24text{ cm}`
`text{To find :}`
`text{The radius & slant height of heap.}`
`text{Solve :}`
`text{According to question}`
`text{Vol. of conical heap = Vol. of Cylindrical bucket}`
`1/3pi(r_1)^2h_1 = pir^2h`
`1/3(r_1)^2times24 = (18)^2times32`
`(r_1)^2 = (3times(18)^2times32)/24`
`(r _1)^2 = (18)^2times4`
`r_1 = sqrt((18)^2times4)`
`r_1 = 18times2`
`r_1 = 36text{ cm}`
`text{slant height }l = sqrt((h_1)^2 + (r_1)^2)`
`text{ }l = sqrt((24)^2+(36)^2)`
`text{ }l = sqrt((12)^2(2^2 + 3^2)`
`text{ }l = 12sqrt(4 + 9)`
`text{ }l = 12sqrt13`
`text{Answer :}`
`text{The radius of conical heap 36 cm and slant height }12sqrt13text{ cm}.`
Q8. Water in a canal, `text{6 m}` wide and `text{1.5 m}` deep, is flowing with a speed of `text{10 km/h}`. How much area will it irrigate in `text{30 minutes},` if `text{8 cm}` of standing water is needed?
`text{Sol. :}`
`text{Given :}`
`text{Cuboid shap canal width }B = 6text{ m}`
`text{Cuboid shap canal depth }H = 1.5text{ m}`
`text{Cuboid shap canal length L = 10km/h}times30/60`
`text{ = 5 km = 5000 m}`
`text{To find :}`
`text{Area irrigate in 30 minutes.}`
`text{Solve :}`
`text{According to question}`
`text{Vol. of water in field = Vol. of water in canal}`
`l times b times h = L times B times H`
`text{Area } times h = 5000 times 6 times 1.5`
`text{Area } times 0.08 = 45000`
`text{Area =}45000/0.08`
`text{ =}(45000 times 100)/(8)`
`text{ =}22500 times 25 text{ m}^2`
`text{ =}562500 text{ m}^2`
`text{ =}56.25 text{ hectare}`
`text{Answer :}`
`text{The area irrigate in 30 minutes 56.25 hectare.}`
Q9. A farmer connects a pipe of internal diameter `text{20 cm}` from a canal into a cylindrical tank in her field, which is `text{10 m}` in diameter and `text{2 m}` deep. If water flows through the pipe at the rate of `text{3 km/h}`, in how much times will the tank be filled?
`text{Sol. :}`
`text{Given :}`
`text{Depth of Cylindrical tank } h = 2 text{ m}`
`text{Diameter of Cylinder tank } d = 10 text{ m}`
`text{Radius of Cylindrical tank }r = 5 text{ m}`
`text{Internal diameter of pipe }d_1 = 20 text{cm =0.2 m}`
`text{Internal radius of pipe }r_1 = 0.1 text{ m}`
`text{The length of water in the pipe in 1 hour }`
`text{ }h = 3text{km = 3000 m}`
`text{To find :}`
`text{The time fill the tank.}`
`text{Solve :}`
`text{Let time to fill is n minutes}`
`text{According to question}`
`text{Vol. of tank = n(Vol. of water in pipe in 1 hour)}`
`pir^2h = n(pir_1^2h_1)`
`r^2h = n(r_1^2h_1)`
`(5)^2times2 = n((0.1)^2times3000)`
`50 = n(30)`
`n = 50/30 text{hours}`
`n = 5/3times60text{ minutes}`
`n = 100text{ minutes}`
`text{Answer :}`
`text{The time fill the tank in 100 minutes}`




Comments