10th Maths 7.1
NCERT Class 10th solution of Exercise 7.2
NCERT Class 10th solution of Exercise 7.3
Exercise 7.1
Q1. Find the distance between the following points:
i) `(2, 3), (4,1)`
ii) `(-5,7), (-1, 3)`
iii) `(a, b), (-a, -b)`
Sol. :
i)
Given:
Let `P(2, 3), Q(4, 1)`
Solve:
Distance `=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`
`PQ=sqrt((4-2)^2+(1-3)^2)`
`PQ=sqrt((2)^2+(-2)^2)`
`PQ=sqrt(4+4)`
`PQ=sqrt8`
`PQ=2sqrt2` units.
Answer:
Distance `2sqrt2` units.
ii)
Given:
Let `P(-5, 7), Q(-1, 3)`
Solve:
Distance `=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`
`PQ=sqrt((-1+5)^2+(3-7)^2)`
`PQ=sqrt((4)^2+(-4)^2)`
`PQ=sqrt(16+16)`
`PQ=sqrt(32)`
`PQ=16sqrt2` units
Answer:
Distance `16sqrt2` units.
iii)
Given:
Let `P(a, b), Q(-a, -b)`
Solve:
Distance `=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`
`PQ=sqrt((-a-a)^2+(-b-b)^2)`
`PQ=sqrt((-2a)^2+(-2b)^2)`
`PQ=sqrt(4a^2+4b^2)`
`PQ=sqrt(4(a^2+b^2))`
`PQ=2sqrt(a^2+b^2)` units
Answer:
Distance `2sqrt(a^2+b^2)` units.
Q2. Find the distance between the points `(0, 0),` and `(36, 15).` Can you now find the distance between the two towns `A` and `B` discussed in section `7.2`.
Given:
Let `A(0, 0), B(36, 15)`
To find:
Distance between two towns `A` and `B`.
Solve:
Distance `=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`
`AB=sqrt((36-0)^2+(15-0)^2)`
`AB=sqrt((36)^2+(15)^2)`
`AB=sqrt(1296+225)`
`AB=sqrt(1521)`
`AB=39` units
Answer:
Distance between two towns `A` and `B` is `39` units.
Q3. Determine if the points `(1, 5), (2, 3)` and `(-2, -11)` are collinear.
Sol. :
Given:
Let `P(1, 5), Q(2, 3), R(-2, -11)`
To find:
Collinear
Solve:
Distance `=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`
`PQ=sqrt((2-1)^2+(3-5)^2)`
`PQ=sqrt((1)^2+(2)^2)`
`PQ=sqrt(1+4)`
`PQ=sqrt5` units
`QR=sqrt((-2-2)^2+(-11-3)^2)`
`QR=sqrt(-4)^2+(-14)^2)`
`QR=sqrt(16+196)`
`QR=sqrt(212)`
`RP=sqrt((1+2)^2+(5+11)^2)`
`RP=sqrt((3)^2+(16)^2)`
`RP=sqrt(9+256)`
`RP=sqrt(265)`
For collinear
`PQ+QR=RP`
But
`sqrt5+sqrt212nesqrt265`
Answer:
The points are not collinear.
Q4. Check whether `(5, -2), (6, 4)` and `(7, -2)` are the vertices of an isosceles triangle.
Sol. :
Given:
Let `P(5, -2), Q(6, 4), R(7, -2)`
To Find:
Points are the vertices of an isosceles triangle.
Solve:
`PQ=sqrt((6-5)^2+(4+2)^2)`
`PQ=sqrt((1)^2+(6)^2)`
`PQ=sqrt(1+36)`
`PQ=sqrt(37)`
`QR=sqrt((7-6)^2+(-2-4)^2)`
`QR=sqrt((1)^2+(-6)^2)`
`QR=sqrt(1+36)`
`QR=sqrt(37)`
`RP=sqrt((7-5)^2+(-2+2)^2)`
`RP=sqrt((2)^2+(0)^2)`
`RP=sqrt4`
`RP=2`
`PQ=QR`
Answer:
Yes, points are the vertices of an isosceles triangle.
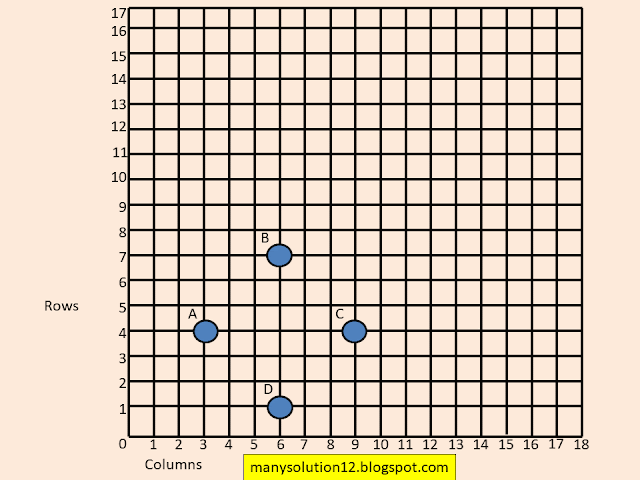
Q5. In a classroom, `4` friends are seated at the points `A, B, C` and `D` as shown in figure. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, ''Don't you think `ABCD` is a square?'' Chameli disagrees. Using distance formula, find which of them is correct.
Given:
`A(3, 4), B(6, 7), C(9, 4), D(6, 1)`
To Find:
Which of them (Champa and Chameli) is correct.
Solve:
Distance formula `=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`
`AB=sqrt((6-3)^2+(7-4)^2)`
`AB=sqrt((3)^2+(3)^2)`
`AB=sqrt(9+9)`
`AB=sqrt18`
`AB=3sqrt2`
`BC=sqrt((9-6)^2+(4-7)^2)`
`BC=sqrt((3)^2+(-3)^2)`
`BC=sqrt(9+9)`
`BC=sqrt(18)`
`BC=3sqrt2`
`CD=sqrt((6-9)^2+(1-4)^2)`
`CD=sqrt((3)^2+(-3)^2)`
`CD=sqrt(9+9)`
`CD=sqrt(18)`
`CD=3sqrt2`
`DA=sqrt((3-6)^2+(4-1)^2)`
`DA=sqrt((-3)^2+(3)^2)`
`DA=sqrt(9+9)`
`DA=sqrt(18)`
`DA=3sqrt2`
This gives
`AB=BC=CD=DA`
So `ABCD` is rhombus.
Diagonals are
`AC=sqrt((9-3)^2+(4-4)^2)`
`AC=sqrt((6)^2+(0)^2)`
`AC=sqrt(36)`
`AC=6`
`BD=sqrt((6-6)^2+(1-7)^2)`
`BD=sqrt((0)^2+(-6)^2)`
`BD=sqrt(36)`
`BD=6`
Diagonal`AC=`Diagonal`BD`
Answer:
`ABCD` is a square and hence Champa is correct.
Q6. Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
i) `(-1, -2), (1, 0), (-1, 2), (-3, 0)`
ii) `(-3, 5), (3, 1), (0, 3), (-1, -4)`
iii) `(4, 5), (7, 6), (4, 3), (1, 2)`
Sol. :
i)
Given:
Let `P(-1, -2), Q(1, 0), R(-1, 2), S(-3, 0)`
Solve:
`PQ=sqrt((1+1)^2+(0+2)^2)`
`PQ=sqrt((2)^2+(2)^2)`
`PQ=sqrt(4+4)`
`PQ=sqrt8`
`PQ=2sqrt2`
`QR=sqrt(-1-1)^2+(2-0)^2)`
`QR=sqrt(-2)^2+(2)^2`
`QR=sqrt(4+4)`
`QR=sqrt(8)`
`QR=2sqrt2`
`RS=sqrt((-3+1)^2+(0-2)^2)`
`RS=sqrt((-2)^2+(-2)^2)`
`RS=sqrt(4+4)`
`RS=sqrt(8)`
`RS=2sqrt2`
`SP=sqrt((-1+3)^2+(-2-0)^2)`
`SP=sqrt((2)^2+(-2)^2)`
`SP=sqrt(4+4)`
`SP=sqrt8`
`SP=2sqrt2`
Diagonals
`PR=sqrt((-1+1)^2+(2+2)^2)`
`PR=sqrt((0)^2+(4)^2)`
`PR=sqrt(16)`
`PR=4`
`QS=sqrt((-3-1)^2+(0-0)^2)`
`QS=sqrt((-4)^2+(0)^2)`
`QS=sqrt(16)`
`QS=4`
Sides `PQ=QR=RS=SP` and diagonals `PR=QS`.
Answer:
Quadrilateral is square.
ii)
Given:
Let `P(-3, 5), Q(3, 1), R(0, 3), S(-1, -4)`
Solve:
`PQ=sqrt((3+3)^2+(1-5)^2)`
`PQ=sqrt((6)^2+(-4)^2)`
`PQ=sqrt(36+16)`
`PQ=sqrt(52)`
`PQ=2sqrt13`
`QR=sqrt((0-3)^2+(3-1)^2)`
`QR=sqrt((-3)^2+(2)^2)`
`QR=sqrt(9+4)`
`QR=sqrt(13)`
`RS=sqrt((-1-0)^2+(-4-3)^2)`
`RS=sqrt((-1)^2+(-7)^2)`
`RS=sqrt(1+49)`
`RS=sqrt(50)`
`RS=5sqrt2`
`SP=sqrt((-3+1)+(5+4)^2)`
`SP=sqrt((-2)^2+(9)^2)`
`SP=sqrt(4+81)`
`SP=sqrt(85)`
`PR=sqrt((0+3)^2+(3-5)^2)`
`PR=sqrt((3)^2+(-2)^2)`
`PR=sqrt(9+4)`
`PR=sqrt13`
`PR+QR=PQ`
`sqrt13+sqrt13=2sqrt13`
Answer:
No quadrilateral is formed.
iii)
Given:
Let `P(4, 5), Q(7, 6), R(4,3), S(1, 2)`
Solve:
`PQ=sqrt((7-4)^2+(6-5)^2)`
`PQ=sqrt((3)^2+(1)^2)`
`PQ=sqrt(9+1)`
`PQ=sqrt(10)`
`QR=sqrt((4-7)^2+(3-6)^2)`
`QR=sqrt((-3)^2+(-3)^2)`
`QR=sqrt(9+9)`
`QR=sqrt(18)`
`QR=3sqrt2`
`RS=sqrt((1-4)^2+(2-3)^2)`
`RS=sqrt(-3)^2+(-1)^2)`
`RS=sqrt(9+1)`
`RS=sqrt(10)`
`SP=sqrt((4-1)^2+(5-2)^2)`
`SP=sqrt((3)^2+(3)^2)`
`SP=sqrt(9+9)`
`SP=sqrt(18)`
`SP=3sqrt2`
`PQ=RS=sqrt10` and `QR=SP=3sqrt2`
Answer:
Parallelogram is formed.
Q7. Find the point on the `x`-axis which is equidistance from `(2, -5)` and `(-2, 9)`.
Sol. :
Given:
Let `P(x, 0), Q(2, -5)` and `R(-2,9)`
To Find:
The point on the `x-`axis.
Solve:
`sqrt((2-x)^2+(-5-0))=sqrt((-2-x)^2+(9-0)^2)`
`sqrt((2-x)^2+(-5)^2)=sqrt((-2-x)^2+(9)^2)`
`(2-x)^2+25=(-2-x)^2+81`
`4-4x+x^2+25=4+4x+x^2+81`
`4x+4x=4+25-4-81`
`8x=-56`
`x=-56/8`
`x=-7`
Answer:
The point on the `x-`axis is `(-7, 0)`.
Q8. Find the values of `y` for which the distance between the points `P(2, -3)` and `Q(10, y)` is `10` units.
Sol. :
Given:
`P(2, -3), Q(10, y)` and `PQ=10` units
To Find:
The value of `y`.
Solve:
`sqrt((10-2)^2+(y+3)^2)=(10)`
Squaring both the sides.
`(8)^2+(y+3)^2=(10)^2`
`64+y^2+6y+9=100`
`y^2+6y73=100`
`y^2+6y-27=0`
`y^2+9y-3y-27=0`
`y(y+9)-3(y+9)=0`
`(y+9)(y-3)=0`
`y=-9, 3`
Answer:
The value of `y` are `-9, 3.`
Q9. If `Q(0, 1)` is equidistant from `P(5, -3)` and `R(x, 6),` find the values of `x`. Also find the distance `QR` and `PR`.
Sol. :
Given:
`Q(0, 1), P(5, -3), R(x,6)` and `QP=QR`.
To Find:
Value of `x` and the distance `QR` and `PR`.
Solve:
`sqrt((x-0)^2+(6-1)^2)=sqrt((5-0)^2+(-3-1)^2)`
`(x)^2+(5)^2=(5)^2+(-4)^2`
`x^2+25=25+16`
`x^2=16`
`x=+-sqrt16`
`x=+-4`
`QR=sqrt((x-0)^2+(6-1)^2)`
`QR=sqrt((x)^2+(5)^2)`
`QR=sqrt((x)^2+25)`
`QR=sqrt(+-4)^2+25)`
`QR=sqrt(16+25)`
`QR=sqrt(41)`
`PR=sqrt((x-5)^2+(6+3)^2)`
`PR=sqrt((x)^2-10x+25+(9)^2)`
When `x=+4`
`PR=sqrt((+4)^2-10(4)+25+81)`
`PR=sqrt(16-40+106)`
`PR=sqrt(82)`
When `x=-4`
`PR=sqrt((-4)-10(-4)+106)`
`PR=sqrt(16+40+106)`
`PR=sqrt(162)`
`PR=9sqrt2`
Answer:
Value of `x=+-4`
The distance `QR=sqrt41` and `PR=sqrt82` or `9sqrt2`.
Q10. Find a relation between `x` and `y` such that the point `(x, y)` is equidistant from the point `(3, 6)` and `(-3, 4)`.
Sol. :
Given:
Let `P(x, y), Q(3, 6)`, and `R(-3, 4)` and `PQ=PR`
To find:
The relation between `x` and `y`.
Solve:
`sqrt((x-3)^2+(y-6)^2)`=sqrt((x+3)^2+(y-4)^2)`
Squaring both the sides
`(x-3)^2+(y-6)^2=(x+3)^2+(y-4)^2`
`x^2-6x+9+y^2-12y+36=x^2+6x+9+y^2-8y+16`
`6x+6x-8y+12y+25-45=0`
`12x+4y-20=0`
`3x+y-5=0`
Answer:
The relation between `x` and `y` is `3x+y-5=0`.



Comments