10th Maths 10.2
NCERT Class 10th solution of Exercise 10.1
NCERT Class 10th Maths Projects
Exercise 10.2
In Q. 1 to 3, choose the correct option and give justification.
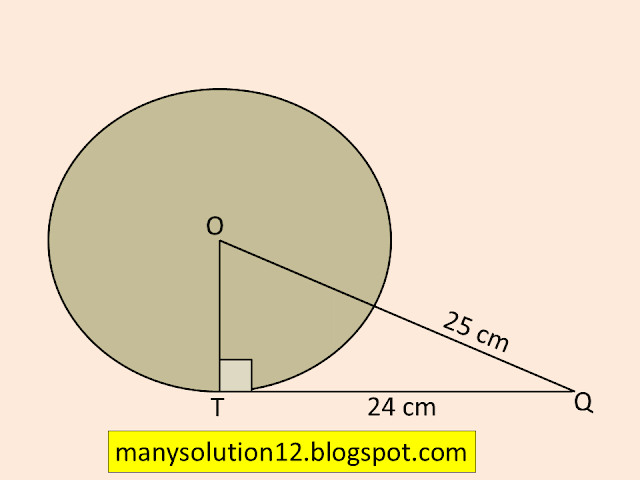
1. From a point `Q,` the length of the tangent to a circle is `24 cm` and the distance of `Q` from the centre is `25 cm.` The radius of the circle is
A) `7 cm` B) `12 cm` C) `15 cm` D) `24.5 cm`
Sol. :
by Pythagoras theorem
`OQ^2 = OT^2 + QT^2`
`(25)^2 = (24)^2 + QT^2`
`625 = 576 + QT^2`
`625 - 576 = QT^2`
`49 = QT^2`
`QT^2 = (7)^2`
`QT = 7`
Answer:
`A)` `7 cm`
2. In figure, If `TP` and `TQ` are the two tangents to a circle with centre `O` so that `angle POQ = 110^circ`, then `angle PTQ` is equal to
A) `60^circ` B) `70^circ` C) `80^circ` D) `90^circ`
Sol. :
`angle POQ + angle OPT + angle OQT + angle PTQ = 360^circ`
`110^circ + 90^circ + 90^circ + angle PTQ = 360^circ`
`290^circ + angle PTQ = 360^circ`
`angle PTQ = 360^circ - 290^circ`
`angle PTQ = 70^circ`
Answer:
`B)` `70^circ`.
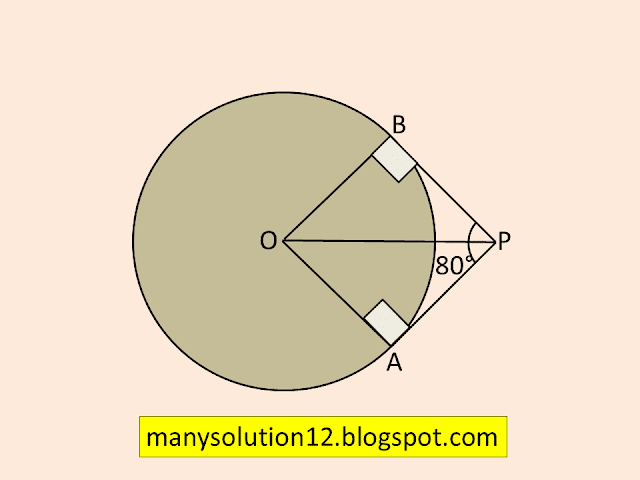
3. If tangents `PA` and `PB` from a point `P` to a circle with centre `O` are each other at angle of `80^circ,` then `anglePOA` is equal to
A) `50^circ` B) `60^circ` C) `70^circ` D) `80^circ`
Sol. :
The line joining the centre of the circle to the external points bisect the angle between the two tangent drawn from the external point.
`angle APO = 1/2 angle APB = 1/2 times 80^circ = 40^circ`
`angle POA = 180^circ - angle APO - angle OPA`
`angle POA = 180^circ - 90^circ - 40^circ`
`angle POA = 180^circ - 130^circ`
`angle POA = 50^circ`
Answer:
`A)` `50^circ`
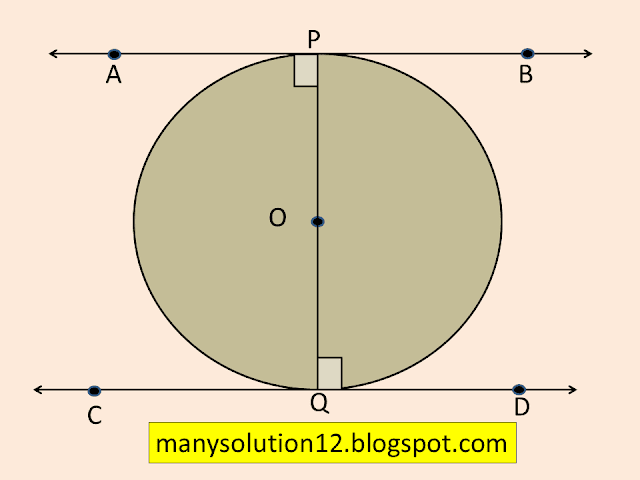
Q4. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Sol. :
Circle `C(O, r),`
`PQ` is the diameter,
`AB, CD` are the tangent
To Prove:
`AB ∥ CD`
Proof:
Radius `OP ⊥` tangent `APB` i.e. `OP ⊥ AB`
`angle APO = 90^circ`
Radius `OQ ⊥` tangent `DQO` i.e. `OQ ⊥ CD`
`angle DQO = 90^circ`
`angle APO = angle DQO`
These are alternate angles
`AB ∥ CD`
The tangents are drawn at the endpoints of a diameter of a circle are parallel.
Proved.
Q5. Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Q5. Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Sol. :
Circle `C(O, r)`
tangent `AB`
`QP ⊥ AB`
To Prove:
`PQ` passes through the point `O`.
Proof:
Suppose `PQ` is not passing through `O`.
Then join `OP`.
`OP ⊥ AB` [Radius `OP ⊥` tangent `APB`]
`QP ⊥ AB` [Given]
This is contradiction i.e. two perpendiculars is not possible through a point on a line on the same side hence `OP` and `QP` coincides.
Proved.
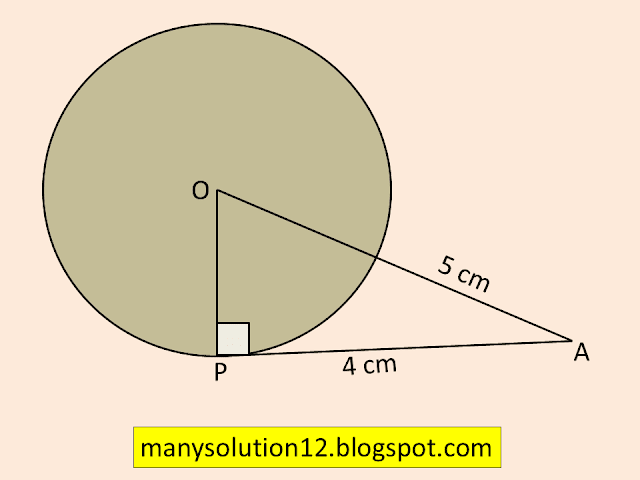
Q6. The length of a tangent from a point `A` at distance `5 cm` from the centre of the circle is `4 cm.` Find the radius of the circle.
Sol. :
By Pythagoras theorem
`OA^2 = OP^2 + AP^2`
`(5)^2 = OP^2 + (4)^2`
`OP^2 = 25 - 16`
`OP^2 = 9`
`OP^2 = (3)^2`
`OP = 3 cm`
`r = 3 cm`
Answer:
The Radius of the circle is `3 cm`.
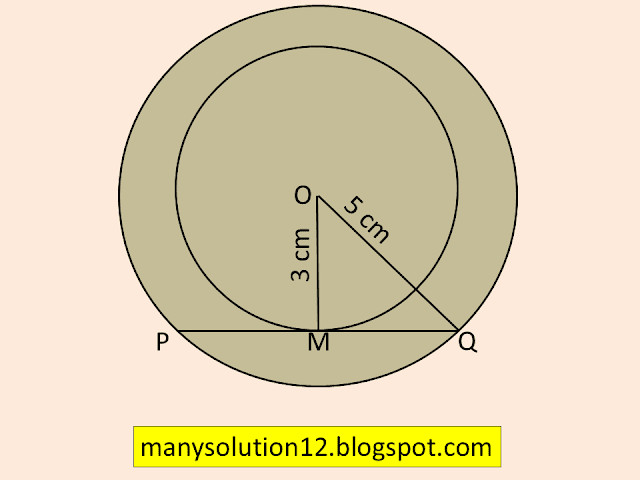
Q7. Two concentric circles are of radii `5 cm` and `3 cm.` Find the length of the chord of the larger circle which touches the smaller circle.
Sol. :
By Pythagoras theorem
`OM^2 = OM^2 + QM^2`
`(5)^2 = (3)^2 + QM^2`
`25 = 9 + QM^2`
`QM^2 = 25 - 9`
`QM^2 = 16`
`QM^2 = (4)^2`
`QM =4 cm`
The perpendicular is drawn from the centre of the circle to chord bisect the chord.
`PQ = 2 times 4`
`PQ = 8 cm`
Answer:
The length of the chord is `8 cm.`
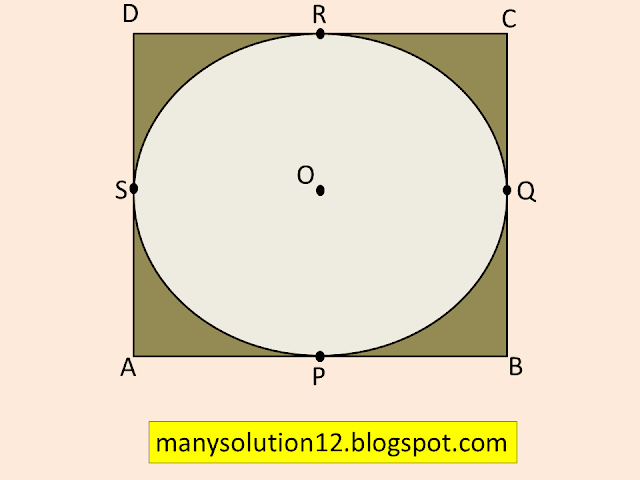
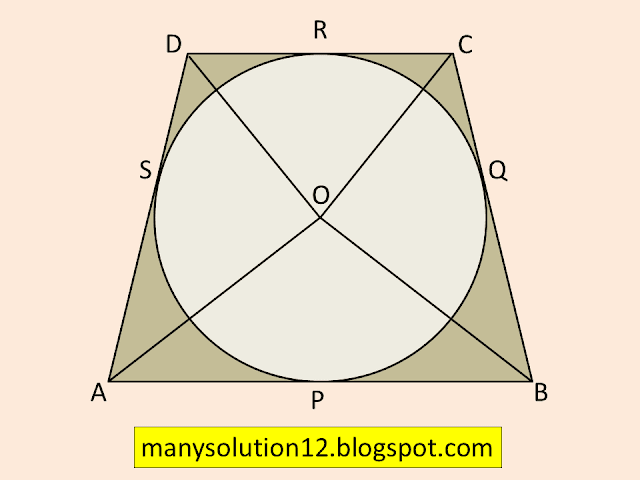
Q8. A quadrilateral `ABCD` is drawn to circumscribe a circle (see figure). Prove that `AB + CD = AD + BC`
Given:
Quadrilateral `ABCD` and Circle touches it at `P, Q, R, S`
To Prove:
`AB + CD = AD + BC`
Proof.
In quadrilateral `ABCD`
The lengths of tangents drawn from an external point to a circle are equal.
`AB` and `AC` are two tangents, and the external point is `A`
So that `AP = AS` _______(1)
`BP` and `BQ` are two tangents, and the external point is `B`
So that `BP = BQ`________(2)
`CR` and `CQ` are two tangents, and the external point is `C`
So that `CR = CQ`________(3)
`DR` and `DS` are two tangents, and the external point is `D`
So that `DR = DS`________(4)
From equations (1) + (2) + (3) + (4)
`AP + BP +CR + DR = AS + BQ + CS + DS`
`AB + CD + CR = AD + BC`
Proved.
Q9. In figure, `XY` and `X'Y'` are two parallel tangents to a circle with centre `O` and another tangent `AB` with point of contact `C` intersecting `XY` at `A` and `X'Y'`at `B`. Prove that `angle AOB = 90^circ.`
Given:
`XY∥X'Y'`are tangents intersected by tangent `AB`
To Prove:
`angle AOB = 90^circ`
Proof:
`angle XAB + angleX'BA = 180^circ`____(1) [interior angles on the same side]
`AX` and `AB` are two tangents drawn from the external point `A` to the circle.
`angle OAB = 1/2angle X'AB`_____(2)
`BX'` and `BA` are two tangents drawn from the external point `B` to the circle.
`angle OBA = 1/2 angle X'BA`_____(3)
from equation (2) + (3)
`angle OAB + angle OBA = 1/2angle X' AB + 1/2 angle X'BA`__(4)
`angle OAB + angle OBA = 1/2(angleX'AB + angleX'BA)`__(5)
`angle OAB + angle OBA = 1/2 times 180^circ`
`angle OAB + angle OBA = 90^circ`___(6)[From eq (5) and (1)]
By angle sum property of `triangle`
`angle OAB + angle OBA + angle AOB = 180^circ`
`90^circ + angle AOB = 180^circ`
`angle AOB = 180^circ - 90^circ`
`angle AOB = 90^circ`
Proved.
Q10. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
Sol. :
Given:
`PQ` and `PR` are tangents and Circle `C(O, r)`
To Prove:
`angle QOR + angle QPR = 180^circ`
Construction:
Join `OP`
Proof:
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
In `triangle PQO,` `angle PQO = 90^circ`
Acute angles of right `triangle`
`angle QOP + angle QPO = 90^circ`____(1)
In `triangle ORP,` `angleORP = 90^circ`
Acute angles of right `triangle`
`angle POR + angle OPR = 90^circ`_____(2)
From equation (1) + (2)
`angle QOP + angle QPO + angle POR + angle OPR = 90^circ + 90^circ`
`angle QOR + angle QPR = 180^circ`
Proved.
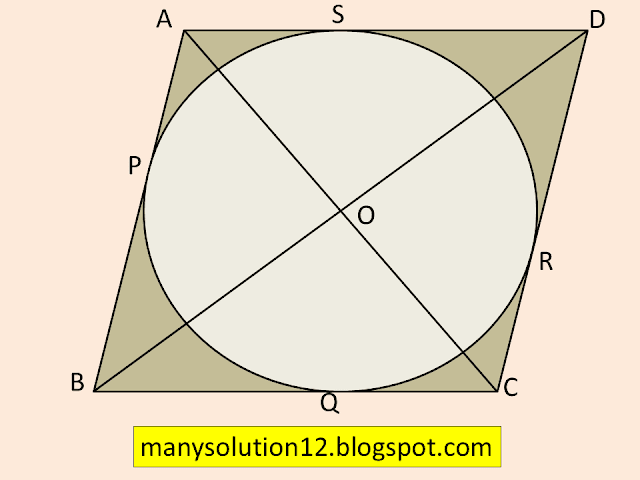
Q11. Prove that the parallelogram circumscribing a circle is a rhombus.
Sol. :
Given:
Quadrilateral `ABCD` and Circle touches it at `P, Q, R, S`
Construction:
Join `OA, OB, OC,` and `OD.`
To Prove:
The parallelogram is a rhombus.
Proof:
In quadrilateral `ABCD`
`AB` and `AD` are two tangents and external point `A` to a circle.
`angle BAO = angle DAO = 1/2 angle BAD`_____(1)
`BA` and `BC` are two tangents and external point `B` to a circle
`angle ABO = angle CBO = 1/2 angle ABC`______(2)
From equation (1) + (2)
`angle ABO + angle ABO = 1/2 angle BAD + 1/2 angle ABC`
`angle ABO + angle ABO = 1/2 (angle BAD + angle ABC)`___(3)
and
Adjacent angles of parallelogram
`angle BAD + angle ABC = 180^circ` ____(4)
from equation (3) and (4)
` angle BAO + angle ABO = 1/2 times 180^circ`___(5)
By angle sum property of `triangle`
`angle BAO + angle ABO + angle AOB = 180^circ`__(6)
Equation (6) - (5)
`angle AOB = 90^circ`
Similarly
`angle BOC = angle COD = angle DOA = 90^circ`
`angle AOB + angle AOD = 180^circ`
`angle AOB + angle BOC = 180^circ`
Diagonal `AC` and `BD` are bisect each other at right angles.
So that
`ABCD` is rhombus.
Proved.
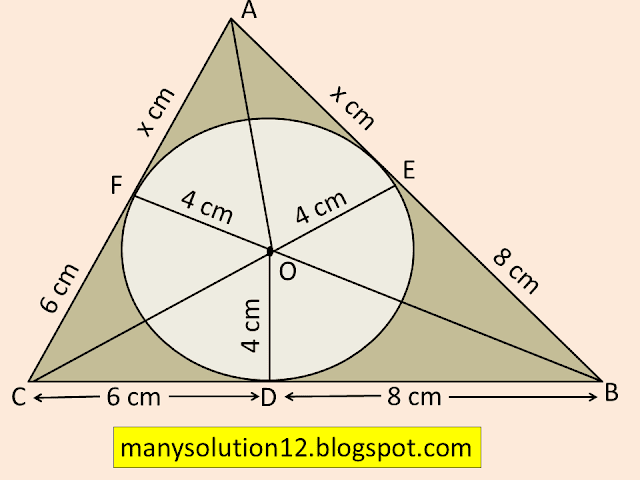
Q12. A triangle `ABC` is drawn to circumscribe a circle of radius `4 cm` such that the segments `BD` and `DC` into which `BC` is divided by the point of contact `D` are of lengths `8 cm` and `6 cm` respectively (see figure). Find the sides `AB` and `AC`.
Given:
`triangle ABC, C(O, r), OD = 4 cm, CD = 6 cm` and `BD = 8 cm`
To Find:
Side `AB` and `AC`
Solve:
Let `AE = AF = x cm`
`ar(OAB) = 1/2 times AB times OE`
`ar(OAB) = 1/2 times (x + 8) times 4`
`ar(OAB) = (2x + 16) cm^2`
`ar(OBC) = 1/2 times BC times OD`
`ar(OBC) = 1/2 times 14 times 4`
`ar(OBC) = 28 cm^2`
`ar(OCA) = 1/2 times CA times OF`
`ar(OCA) = 1/2 times (x + 6) times 4`
`ar(OCA) = (2x+12) cm^2`
`ar(ABC) = ar(OAB) + ar(OBC) + ar(OCA)`
`ar(ABC) = (2x + 16) + 28 + (2x + 12)`
`ar(ABC) = 4x + 56`
`S = (a+b+c)/2`
`=(14 + x + 6 + x + 8)/2 = (x + 14) cm`
`ar(ABC)`
`= sqrt((x+14)(x+14-14)(x+14-x-6)(x+14-x-8))`
`4(x + 14)= sqrt((x+14)(x)(8)(6))`
`4(x + 14)= sqrt(16(3x^2 + 42x))`
`4(x + 14)= 4sqrt(3x^2 + 42x)`
`x+14 = sqrt(3x^2 +42x)`
`(x + 14)^2 = 3x^2 +42x`
`x^2 +28x +196 =3x^2 +42x`
`2x^2+14x-196 =0`
`x^2+7x-98=0`
`x^2+14x-7x-98=0`
`x(x+14)-7(x+14)=0`
`(x-7)(x+14)=0`
`x =7`
`x= -14` [ It is not possible]
`AB =x+8 =7+8 =15 cm`
`AC =x+6 =7+6 =13 cm`
Answer:
`AB = 15 cm` and `AC = 13 cm`
Q13. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angle at the centre of the circle.
Sol. :
Quadrilateral `ABCD` and Circle touch its point `P, Q, R, S`
To Prove:
`angle DOC + angle AOB =180^circ`
Construction:
Join `DO, AO, OB, OC`
Proof:
The lengths of tangents drawn from an external point to a circle are equal.
`angleCOD = angleADO = 1/2angleD`_____(1)
`angleDAO = angleBAO = 1/2angleA`_____(2)
`angleABO = angleCBO = 1/2angleB`______(3)
`angleBCO = angleDCO = 1/2angleC`______(4)
By sum of interior angles of quadrilateral.
`angleA+angleB+angleC+angleD=360^circ`
`1/2angleA+1/2angleB+ 1/2angleC+1/2angleD = 180^circ`___(5)
In `triangle DOC`
`angleDOC+angleCDO+angleDCO=180^circ`____(6)
By eq. (1), (4) and (6)
`angleDOC+1/2angleD+1/2angleC=180^circ`____(7)
In `triangleAOB`
`angleAOB+angleABO+angleBAO=180^circ`_____(8)
By eq. (2), (3) and (8)
`angleAOB+1/2angleB+angle1/2angleA=180^circ`__(9)
`angleDOC+angleAOB`
By eq. (7) and (9)
`=1/2angleA+1/2angleB+1/2angleC+1/2angleD=360^circ`__(10)
By eq. (10) - (5)
`angleDOC+angleAOB=180^circ`
Proved.







Comments