10th Maths 14.3
Chapter 14
Statistics
NCERT Class 10th solution of Exercise 14.1
NCERT Class 10th solution of Exercise 14.2
Exercise 14.3
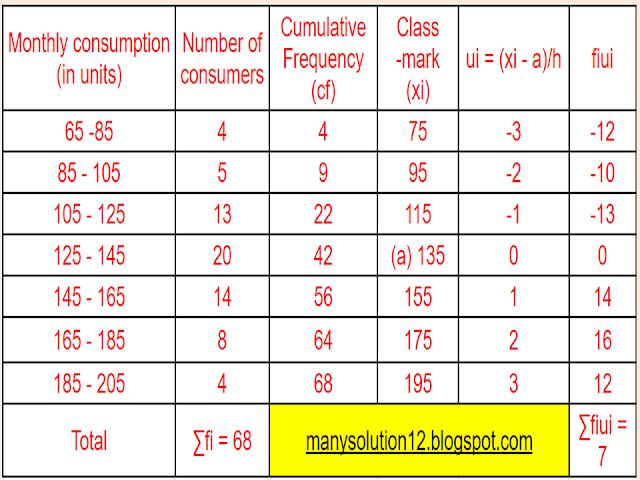
Q1. The following frequency distribution gives the monthly consumption of electricity of `68` consumers of a locality. Find the median, mean, and mode of the data and compare them.
Sol. :
`text{For Median}`
`text{Median } = n/2 = 68/2 = 34^text(th) text{ term}`
`text{Median class is (125—145)}`
`text{lower limit } l = 125`
`text{class-size } h = 145—125 = 20`
`cf = 22`
`text{Median}` `= l + ((n/2 - cf)/f) times h`
`text{Median}` `= 125 + ((68/2 - 22)/ 20) times 20`
`text{Median}` `= 125 + (34 - 22)`
`text{Median}` `= 125 + 12`
`text{Median}` `=137 text{ units}`
`text{For Mean}`
`text{Assume mean }` `a = 135`
`text{class-size }` `h = 20`
`text{Mean }overline x = a +((∑f_iu_i)/(∑f_i)) times h`
`overline x = 135 +((7 times 20)/68)`
`overline x = 135 + 140/68`
`overline x = 135 + 2.06`
`overline x = 137.06 text{ units (approx.)}`
`text{For Mode}`
`text{Modal class is (125—145)}`
`text{lower limit}` ` l = 125`
`text{class-size}` `h = 145—125 = 20`
`text{frequency}` `f_1 = 20`
`text{frequency just before class}` `f_0 = 13`
`text{frequency just after class}` `f_2 = 14`
`text{Mode Z}` `= l + ((f_1 - f_0)/(2f_1 - f_0 - f_2)) times h`
`text{Mode Z}` `= 125 + ((20 - 13)/(2times20 - 13 - 14)) times20`
`text{Mode Z}` `= 125 + (7 times 20)/(40 - 77)`
`text{Mode Z}` `= 125 + 140/13`
`text{Mode Z}` `= 125 + 10.77`
`text{Mode Z}` `= 135.77 text{ units (approx.)}`
`text{Answer:}`
`text{Median = 137 units, Mean = 137.05 units, Mode = 135.76 units}.`
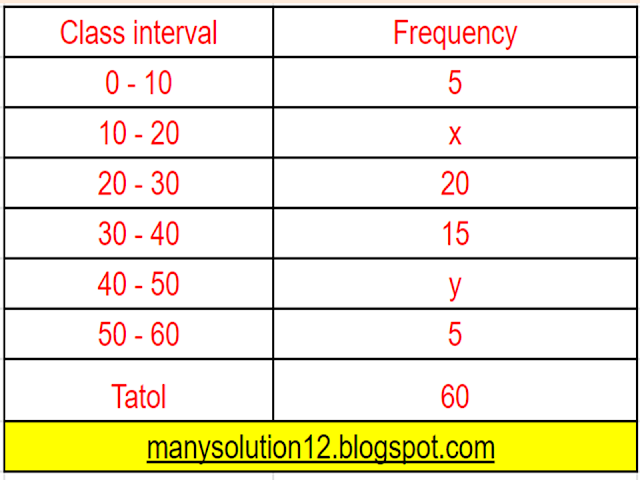
Q2. If the median of the distribution given below is `28.5`, find the value of `x` and `y`.
Sol. :
`45 + x + y = 60`
`x + y = 60 - 45`
`x + y = 15`________(1)
`text{Median} = 28.5`
`text{Medain class} = (20 - 30)`
`text{lower limit } l = 20`
`text{Frequency } f = 20`
`text{Cumulative frequency } cf = 5 + x`
`text{class size} h = 10`
`n = 60`
`text{Median}` `= l + ((n/2 - cf)/(f)) times h`
`28.5 = 20 + ((60/2 - (5 + x))/(20)) times 10`
`57 = 40 + 30 - 5 - x`
`57 = 40 + 25 - x`
`57 = 65 - x`
`x = 65 - 57`
`x = 8`_________(2)
`8 + y = 15` [ from eq. (1) and (2)]
`y = 15 - 8`
`y = 7`
`text{Answer:}`
`text{value of x = 8 and y = 7}.`
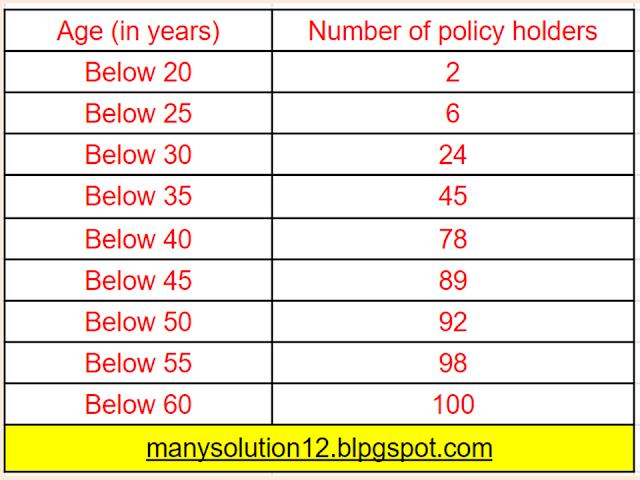
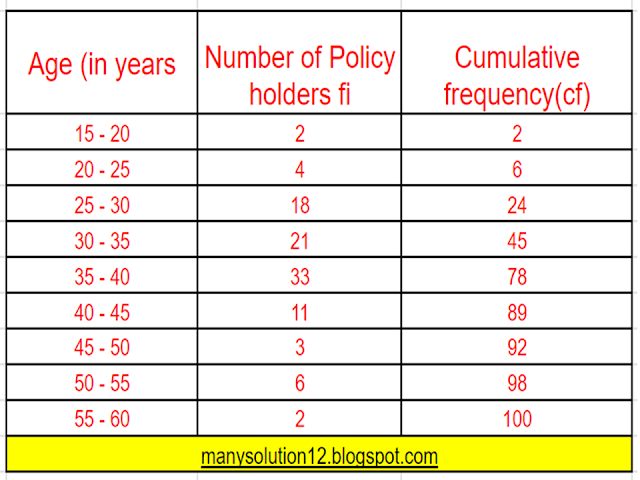
Q3. A life insurance agent found the for distribution of ages of `100` policy holders. Calculate the median age, if policies are given only to persons having age `18` years onwards but less than `60` year.
Sol. :
`text{Median} = n/2 = 100/2 = 50^text(th) text{ term}`
`text{median class} = (35 - 40)`
`text{lower limit } l = 35`
`text{Cumulative frequency } cf = 45`
`text{Frequency } f = 33`
`text{class size } h = 40 - 35 = 5`
`text{Median}``= l + ((n/2 - cf)/f) times h`
`text{Median}``= 35 + ((50 - 45)/33) times 5`
`text{Median}``= 35 + (5times5)/33`
`text{Median}``= 35 + 25/33`
`text{Median}``= 35 + 0.76 = 35.76`
`text{Answer:}`
`text{Median age = 35.76 years`.
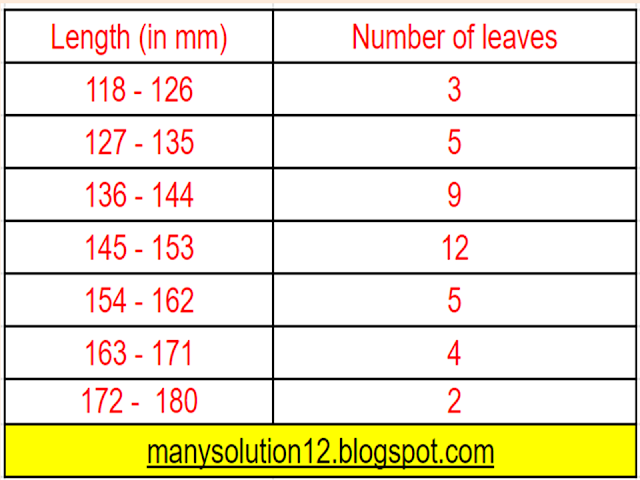
Q4. The lengths of `40` leaves of a plants are measured correct to the nearest millimetre, and the data obtained is represented in the following table:
Find the median length of the leaves.
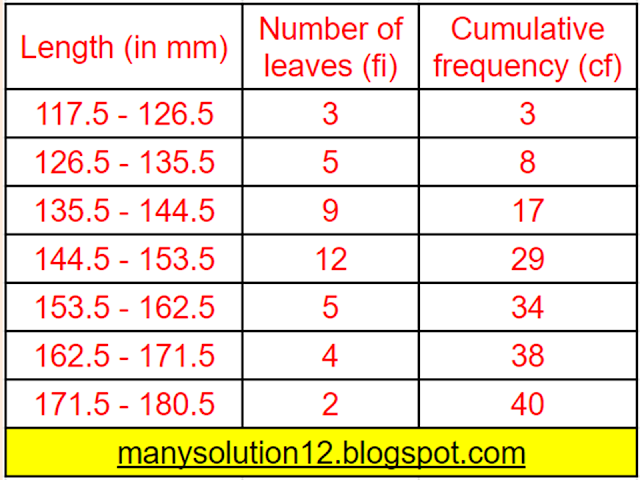
(Hint: The data needs to be converted to continuous classes for finding the median, since the formula assumes continuous classes. The classes then change to `117.5 - 126.5,` `126.5 - 135.5,`...,`171.5 - 180.5`.)
Sol. :
`text{Median}``=n/2 = 40/2 = 20^text (th) text{ term}`
`text{Median class}= (144.5 - 153.5)`
`text{Lower limit } l = 144.5`
`text{class size } h = 153.5 - 144.5 = 9`
`text{Frequency } f = 12`
`text{Cumulative frequency } cf = 17`
`text{Median}`` = l + ((n/2 - cf)/(f)) times h`
`text{Median}`` = 144.5 + (20 - 17)/(12) times 9`
`text{Median}`` = 144.5 + (3 times 9)/12`
`text{Median}`` = 144.5 + 27/86`
`text{Median}`` = 144.5 + 2.25`
`text{Median} = 146.75 text{ mm}`
`text{Answer:}`
`text{Median length} = 146.75 text{ mm}`
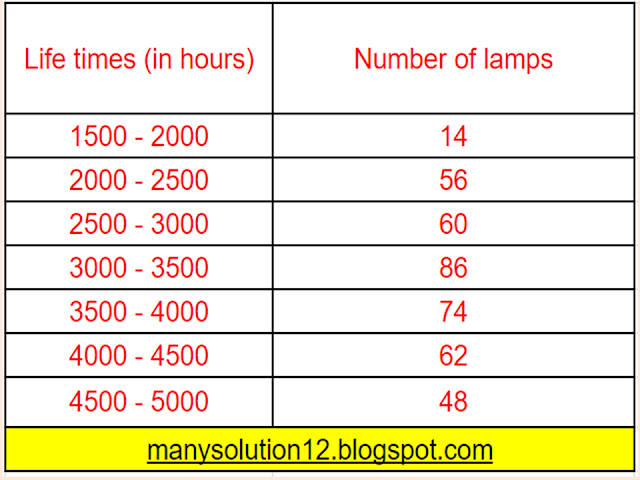
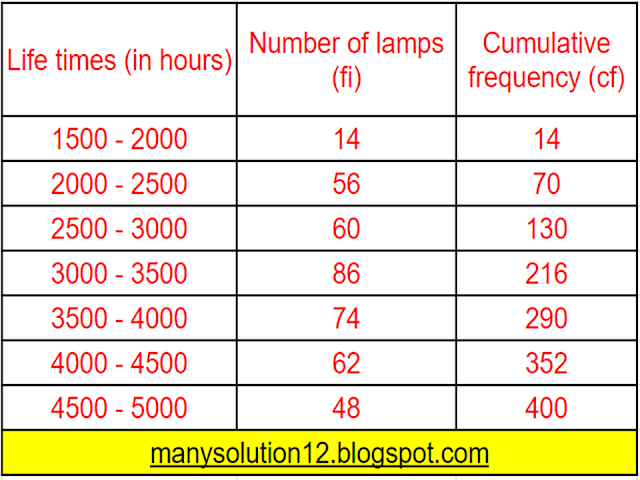
Q5. The following table gives the distribution of the life time of `400` neon lamps:
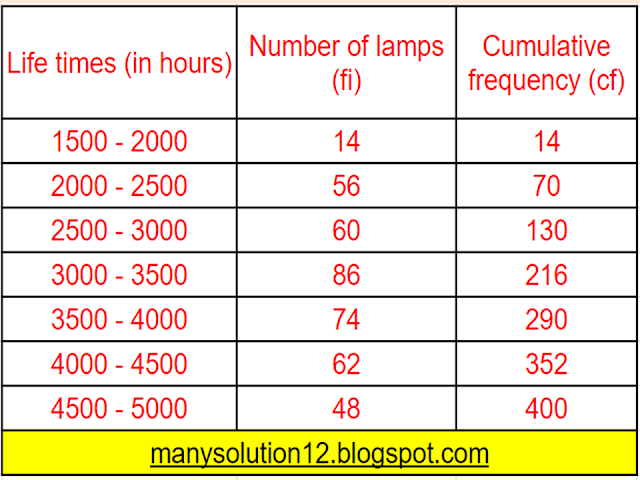
Find the median life time of a lamp.
Sol. :
`text{Median}``=n/2 = 400/2 = 200^text(th) text{ term}`
`text{Median class}= (3000 - 3500)`
`text{Lower limit } l = 3000`
`text{class size } h = 3500 - 3000 = 500`
`text{Frequency } f = 86`
`text{Cumulative frequency } cf = 130`
`text{Median}`` = l + ((n/2 - cf)/(f)) times h`
`text{Median}`` = 3000 + (200 - 130)/(86) times 500`
`text{Median}`` = 3000 + (70 times 500)/86`
`text{Median}`` = 3000 + 35000/86`
`text{Median}`` = 3000 + 406.98`
`text{Median}`` = 3406.98 text{ hours (approx)}`
`text{Answer;}`
`text{Median life}``= 3406.98 text{ hours (approx)}`
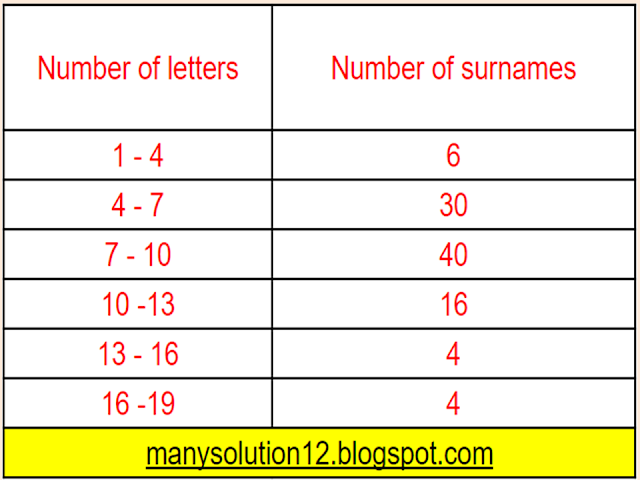
Q6. `100` surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:
Determine the median number of letters in the surnames. Find the mean number of letters in the surnames? Also, find the modal size of the surnames.
Sol. :
`text{For Median}`
`text{Median } = n/2 = 100/2 = 50^text(th) text{ term}`
`text{Median class is (7 - 10)}`
`text{lower limit } l = 7`
`text{class-size } h = 10 - 7 = 3`
`text{Frequency} f = 40`
`cf = 36`
`text{Median}` `= l + ((n/2 - cf)/f) times h`
`text{Median}` `= 7 + ((50 - 36)/ 40) times 3`
`text{Median}` `= 7 + (14 times 3)/40`
`text{Median}` `= 7 + 21/20`
`text{Median}` `= 7 + 1.05`
`text{Median}` `= 8.05 text{ units}`
`text{For Mean}`
`text{Assume mean }` `a = 8.5`
`text{class-size }` `h = 3`
`text{Mean }overline x = a +((∑f_iu_i)/(∑f_i)) times h`
`overline x = 8.50 +((- 6 times 3)/100)`
`overline x = 8.50 - 18 /100`
`overline x = 8.50 - 0.18`
`overline x = 8.32 text{ units }`
`text{For Mode}`
`text{Modal class is (7 - 10)}`
`text{lower limit}` ` l = 7`
`text{class-size}` `h = 10 - 7 = 3`
`text{maximum frequency}` `f_1 = 40`
`text{frequency just before class}` `f_0 = 30`
`text{frequency just after class}` `f_2 = 16`
`text{Mode Z}` `= l + ((f_1 - f_0)/(2f_1 - f_0 - f_2)) times h`
`text{Mode Z}` `= 7 + ((40 - 30)/(2times40 - 30 - 16)) times 3`
`text{Mode Z}` `= 7 + (10 times 3)/(80 - 46)`
`text{Mode Z}` `= 7 + 30/34`
`text{Mode Z}` `= 7 + 15/17`
`text{Mode Z}` `= 7 + .88`
`text{Mode Z}` `= 7.88 text{ units (approx.)}`
`text{Answer:}`
`text{Median = 8.05, Mean = 8.32, Modal size = 7.88}.`
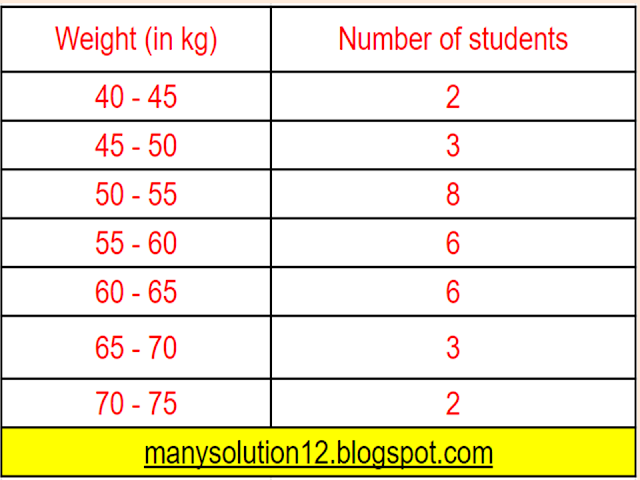
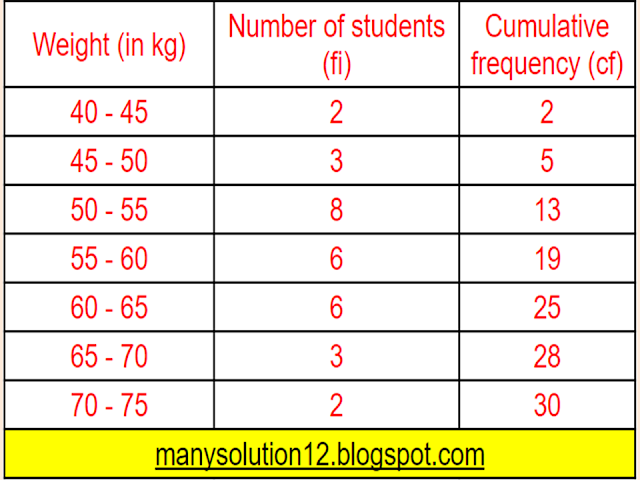
Q7. The distribution below gives the weights of `30` students of a class. Find the median weight of the students.
`text{Median } = n/2 = 30/2 = 15^text(th) text{ term}`
`text{Median class is (55 - 60)}`
`text{lower limit } l = 55`
`text{class-size } h = 60 - 50 = 5`
`text{Frequency} f = 6`
`cf = 13`
`text{Median}` `= l + ((n/2 - cf)/f) times h`
`text{Median}` `= 55 + ((15 - 13)/ 6) times 5`
`text{Median}` `= 55 + (2 times 5)/6`
`text{Median}` `= 55 + 10/6`
`text{Median}` `= 55 + 1.67`
`text{Median}` `= 56.67 text{(approx)}`
`text{Answer:}`
`text{Median} = 56.67 text{ kg (approx)}.`





Comments