10th Maths 13.2
NCERT Class 10th solution of Exercise 13.1
NCERT Class 10th solution of Exercise 13.3
Chapter 13
Surface Areas And Volume
Exercise 13.2
Unless stated otherwise, take `pi = 22/7`.
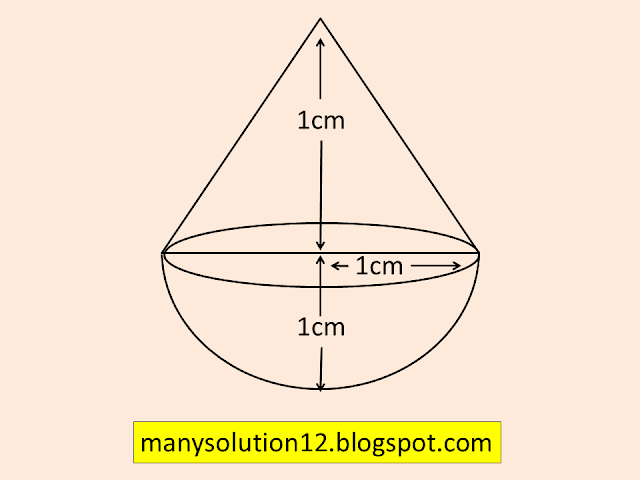
Q1. A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to `text{1 cm}` and the height of the cone is equal to its radius. Find the volume of the solid in terms of `pi`.
`text{Sol. :}`
`text{Given :}`
`text{Radius of Cone & hemisphere } r = 1text{ cm}`
`text{Height of Cone & hemisphere } h = r =1text{ cm}`
`text{To find :}`
`text{Volume of the solid}`
`text{Solve :}`
`text{Volume of Solid = Volume of hemisphere}`
`text{ + Volume of Cone}`
`text{V} = 2/3pir^3 + 1/3pir^2h`
`text{ }= pir^2(2/3r + 1/3h)`
`text{ }= pi(1)^2(2/3times1 + 1/3 times 1)`
`text{ }= pi(2/3 + 1/3)`
`text{ }= pi((2+1)/3)`
`text{ }= pi(3/3)`
`text{ }= pi text{ cm}^3`
`text{Answer :}`
`text{Volume of the solid is } pi text{ cm}^3.`
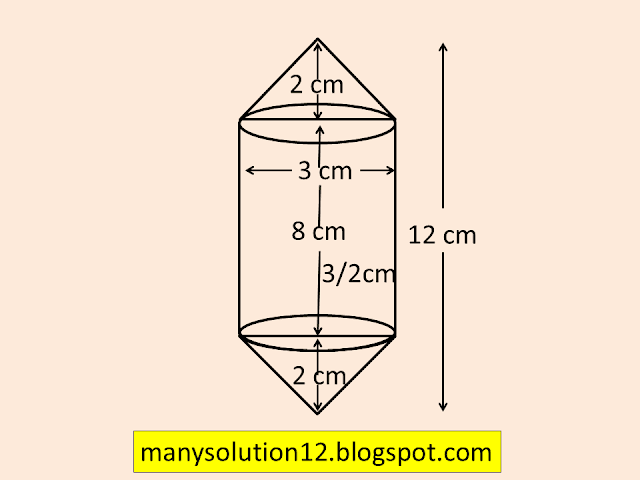
Q2. Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is `text{3 cm}` and its length is `text{12 cm}`. If each cone has a height of `text{2 cm}`, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)
`text{Sol. :}`
`text{Height of each Cone }h = 2 text{ cm}`
`text{Height of Cylinder } H = 12-(2+2)=8text{ cm}`
`text{Radius of Cone & Cylinder }r = 3/2text{ cm}`
`text{To find :}`
`text{Volume of the model}`
`text{Solve :}`
`text{Volume of model = Volume of Cylinder}`
`text{ + }2times text {Volume of Cone}`
`text{V }= pir^2H + 2times1/3pir^2h`
`text{ }= pir^2(H + 2times1/3rh)`
`text{ }= 22/7times(3/2)^2(8 + 2/3times2)`
`text{ }= 22/7times3/2times3/2(8+4/3)`
`text{ }= 11/7times3times3/2((24+4)/3)`
`text{ }= 11/7times3/2times28`
`text{ }= 11times3times2`
`text{ }= 66text{ cm}^3`
`text{Answer :}`
`text{The Volume of the air 66 cm}^3.`
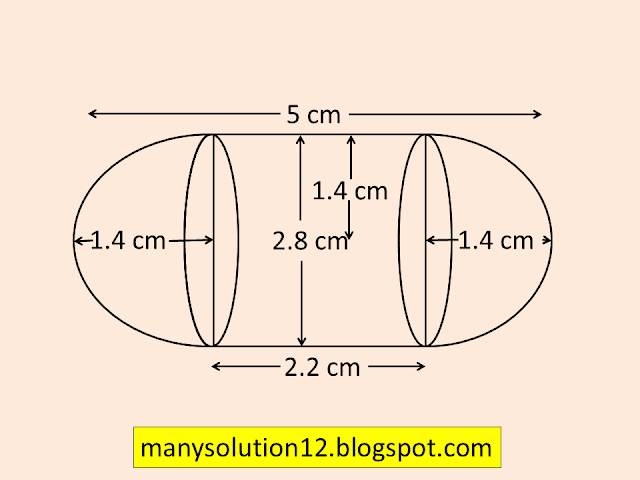
Q3. A gulab jamun contains sugar syrup up to about `30%` of its volume. Find approximately how much syrup would be found in `45` gulab jamuns, each shaped like a cylinder with two hemispherical ends with length `text{5 cm}` and diameter `text{2.8 cm}`(see Figure).
`text{Sol. :}`
`text{Diameter of hemisphere & Cylinder }d = 2.8text{ cm}`
`text{Radius of hemisphere & Cylinder }r = 1.4text{ cm}`
`text{Length of Cylinder }h = 5 - 2(1.4) = 2.2text{ cm}`
`text{To find :}`
`text{Volume of syrup}`.
`text{Solve :}`
`text{Volume of a gulab jamun = Volume of Cylinder}`
`text{ + 2Volume of hemishere}`
`text{V} = pir^2h + 2times2/3pir^3`
`text{ } = pir^2(h + 2times2/3r)`
`text{ } = 22/7times(1.4)^2(2.2 + 2times2/3times1.4)`
`text{ } = 22/7times1.4times1.4(2.2 + (4times1.4)/3)`
`text{ } = 22times1.4times0.2((6.6 + 5.6)/3)`
`text{ } = 22times0.28times(12.2)/3`
`text{ } = 6.16times12.2/3`
`text{ } = 75.152/3`
`text{Total Volume of 45 gulab jamun} = 45 times 75.152/3`
`text{ } = 15times75.152`
`text{ } = 1127.28text{cm}^3`
`text{Volume of syrup} = 30% times text{Total Volume}`
`text{ } = 30/100 times 1127.28`
`text{ } = 338.184text{cm}^3`
`text{Answer :}`
`text{Volume of syrup 338.184 cm}^3`.
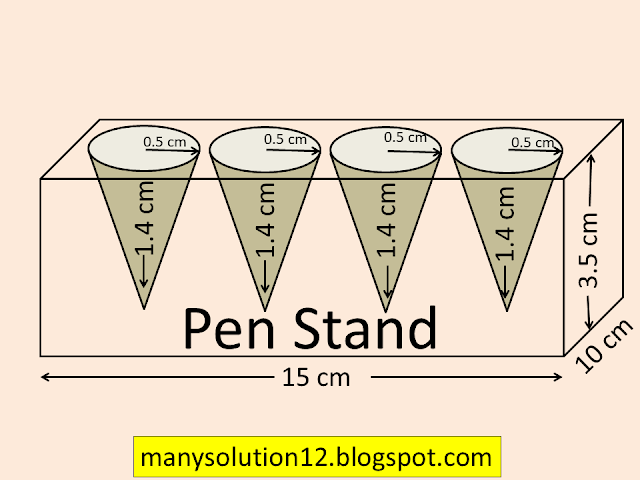
Q4. A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are `text{15 cm by 10 cm by 3.5 cm.}` The radius of each of the depressions is `text{0.5 cm}` and the depth is `text{1.4 cm}`. Find the volume of wood in the entire stand (see figure).
`text{Sol. :}`
`text{Given :}`
`text{Dimensions of the cuboid 15 cm, 10 cm, 3.5 cm}`
`text{Radius of dipressions }r =0.5text{ cm}`
`text{Depth of dipressions }h = 1.4text{ cm}`
`text{To find :}`
`text{The volume of wood in the entire stand.}`
`text{Solve :}`
`text{Volume of wood = Volume of cuboid}`
`text{ - Volume of 4 conical dipression}`
`text{V} = LtimesBtimesH - 4times1/3pir^2h`
`text{} = 15times10times3.5 - 4times1/3times22/7times(0.5)^2times1.4`
`text{} = 525 - 4times1/3times22times0.25times0.2`
`text{} = 525 - 1.47`
`text{} = 523.53text{cm}^3`
`text{Answer :}`
`text{The Volume of wood 523.53 cm}^3.`
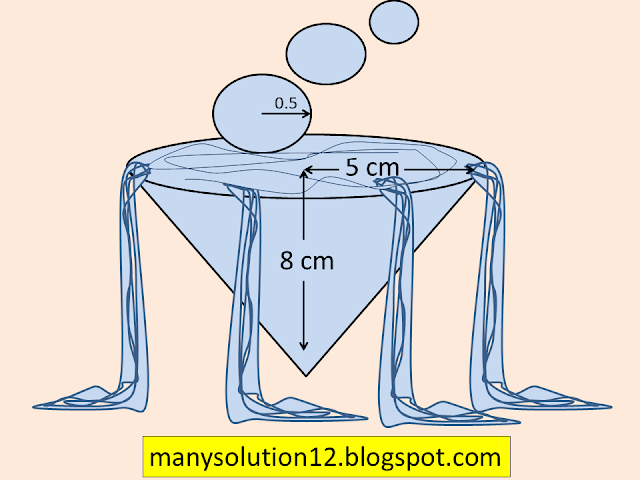
Q5. A vessel is in the form of an inverted cone. Its height is `text{8 cm}` and the radius of its top, which is open, is `text{5 cm.}` It is filled with water up to the brim. When lead shots, each of which is a sphere of radius `text{0.5 cm}` are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
`text{Sol. :}`
`text{Given :}`
`text{Radius of Cone }R = 5text{cm}`
`text{Height of Cone }h = 8text{cm}`
`text{Radius of Sphere }r = 0.5text{cm}`
`text{To find :}`
`text{The number of lead shots dropped in the vessel.}`
`text{Solve :}`
`text{Volume of Conical vessel} = 1/3piR^2h`
`text{V} = 1/3pi(5)^2times8`
`text{ } = 200/3pi`
`text{Volume of water flown out }V_1 = 1/4timesV`
`V_1 = 1/4times200/3pi`
`V_1 = 50/3pi`
`text{The Vol. of n lead shots = Vol. of water displaced}`
`ntimes4/3pi(r)^3 = V_1`
`ntimes4/3pi(0.5)^3 = 50/3pi`
`n = (50times3)/(3times4times0.125)`
`n = (50)/(4times0.125)`
`n = 50/0.5`
`n = 500/5`
`n = 100`
`text{Answer :}`
`text{The number of lead shots in vessel are 100}`.
Q6. A solid iron poe consists of a cylinder of height `text{220 cm}` and base diameter `text{24 cm},` which is surmounted by another cylinder of height `text{60 cm}` and radius `text{8 cm}`. Find mass of the pole, given that `text{1 cm}^3` of iron has approximately `text{8 g}` mass. (Use `pi = 3.14`)
`text{Sol. :}`
`text{Given :}`
`text{Height of Cylindrical pole }h_1 = 220text{ cm}`
`text{Diameter of Cylindrical pole }d= 24text{ cm}`
`text{Radius of Cylindrical pole }r_1 = 12text{ cm}`
`text{Height of another Cylinder }h_2 = 60text{ cm}`
`text{Radius of another Cylinder }r_2 = 8text{ cm}`
`text{To find :}`
`text{The mass of the pole}.`
`text{Solve :}`
`text{Tota Vol. of pole = Vol. of Pole I+Vol. of Pole II}`
`text{V} = pir_1^2h_1 + pir_2^2h_2`
`text{ } = pi(r_1^2h_1 + r_2^2h_2)`
`text{ } = 3.14((12)^2times220 + (8)^2times60)`
`text{ } = 3.14(144times220 + 64times60)`
`text{ } = 3.14(31680 + 3840)`
`text{ } = 3.14(35520)`
`text{ } = 111532.8 text{cm}^3`
`text{mass of iron pole = V}timesRate`
`text{mass of iron pole = }111532.8times 8`
`text{ = 892262.4 g}`
`text{ = 892.26 kg (approx)}`
`text{Answer :}`
`text{The mass of iron pole is 892.26 kg (approx)}.`
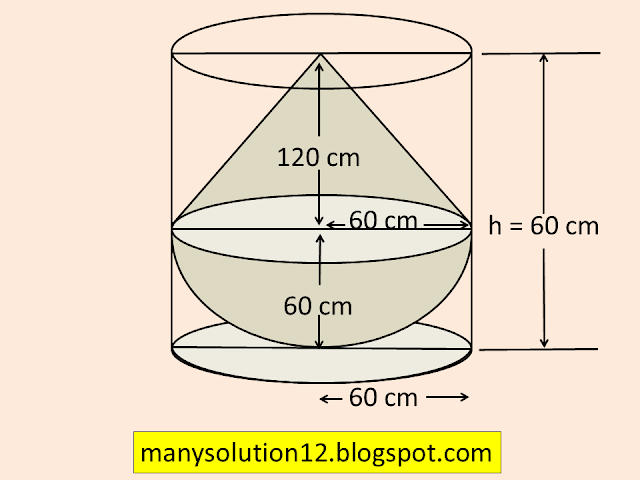
Q7. A solid consisting of a right circular cone of height `text{120 cm}` and radius `text{60 cm}` standing on a hemisphere of radius `text{60 cm}` is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is `text{60 cm}` and its height is `text{180 cm}`.
`text{Sol. :}`
`text{Given :}`
`text{Height of Cylinder }H = 180text{ cm}`
`text{Radius of Cylinder, Cone & hemi. }r = 60text{ cm}`
`text{Heigth of Cone }h = 180 - 60 = 120text{ cm}`
`text{To find :}`
`text{The Volume of water left in the cylinder}`
`text{Solve :}`
`text{Vol. of water = Vol. of Cylinder}`
`text{ - (Vol. of Cone + Vol. of hemisphere)}`
`text{V} = pir^2H - (1/3pir^2h + 2/3pir^3)`
`text{ } = pir^2[H - 1/3(h + 2r)]`
`text{ } = 22/7(60)^2[180 - 1/3 (120 + 2times60)]`
`text{ } = 22/7times3600[180 - 1/3(120 + 120)]`
`text{ } = 11314.285[180 - 1/3times240]`
`text{ } = 11314.285[180 - 80]`
`text{ } = 11314.285times100`
`text{ } = 1131428.500text{ cm}^3`
`text{ } = 1.131text{ m}^3`
`text{Answer :}`
`text{The Vol. of the water left in Cylinder 1.131 m}^3.`
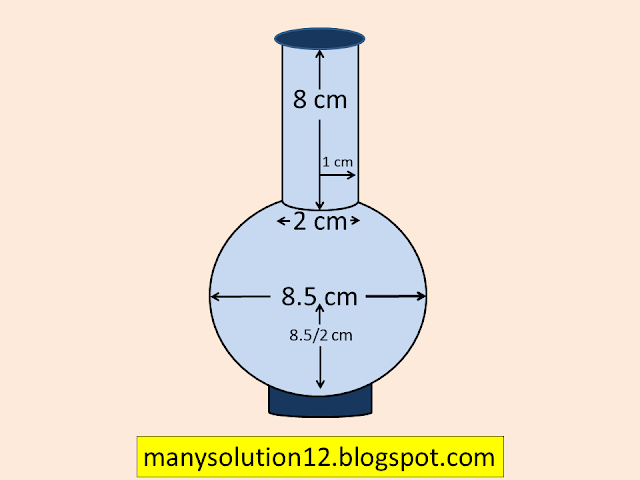
Q8. A spherical glass vessel has a cylindrical neck `text{8 cm}` long, `text{2 cm}` in diameter, the diameter of the spherical part is `text{8.5 cm}`. By measuring the amount of water it holds, a child finds its volume to be `text{345 cm}^3`. Check whether she is correct, taking the above as the inside measurements, and `pi = 3.14`.
`text{Sol. :}`
`text{Given :}`
`text{Diameter of spherical part }D = 8.5text{ cm}`
`text{Radius of spherical part }R = 8.5/2text{ cm}`
`text{Diameter of Cylindrical part }d = 2text{ cm}`
`text{Radius of Cylindrical part }r = 1text{ cm}`
text{Height of Cylindrical part }h = 8text{ cm}`
`text{To find :}`
`text{Volume of Vessel}`
`text{Solve :}`
`text{Total Vol. of Vessel = Vol. of Sphere}`
`text{ + Vol. of Cylinder}`
`text{V} = 4/3piR^3 + pir^2h`
`text{ } = pi(4/3R^3 + r^2h)`
`text{ } = 3.14(4/3times(8.5/2)^3 + (1)^2times8)`
`text{ } = 3.14(4/3times76.76 + 8)`
`text{ } = 3.14(102.35 + 8)`
`text{ } = 3.14times110.35`
`text{ } = 346.51text{ cm}^3`
`text{Answer :}`
`text{Volume of vessel is 346.51 cm}^3`.




Comments