10th Maths Projects
10th Maths Projects
Quick links ↓
NCERT Class 10th solution of Exercise 1.1
Like, Share, and Subscribe.
NCERT Class 10th SSt Project
10th Project Topics
1. Description of the number system with examples.
2. Biography of famous Indian mathematician Srinivasa Ramanujan and contribution in the field of mathematics.
3. Review of perimeter and area of the circle with a diagram and example.
4. Presentation of 30 days of recorded daily maximum temperature data in your city in the form of a graded frequency table and measurement of the mean of these data.
5. `π` is the most mysterious number in the world.
6. Geometric applications in daily life.
7. Find out the HCF of 02 numbers experimentally on the basis of Euclid's division algorithm.
8. To verify the consistent/inconsistent conditions of a pair of linear equations in two variables by graphical method.
9. Verification of distance formula by graphical method.
10. To find the sum of the first n natural numbers.
11. Explain the surface area of a combination of solids with two examples.
12. Establish the trigonometric identities and use these identities to express the trigonometric ratios in terms of other trigonometric ratios.
13. Explain the volume of a combination of solids with two examples.
14. Explain the conversion of a solid from one shape to Another with two examples.
15. Explain the Mean of Grouped Data by Step deviation method.
16. Explain the Mode of Grouped Data with two examples.
17. Explain the Median of Grouped Data with two examples.
18. Describe the Arithmetic Progressions with the help of examples.
19. Establish the Relationship between Zeroes and Coefficients of Polynomials and give two examples.
20. Describe the nth term of an AP with the help of two examples.
Project No. 1
Objective: Description of number system with examples.
Number System
Click the link for Number System
========X=======
Project No. 2
Objective: Biography of famous Indian mathematician Srinivasa Ramanujan and their contribution to the field of mathematics.
Srinivasa Ramanujan
Biography:
Ramanujan was born on 22 December 1887 in Erode India, a small village about 400 km southwest of Madras (Chennai).
When he was 15 years old he obtained a copy of George Shoobridge Carr's Synopsis of Elementary Results in Pure and Applied Mathematics 2 vol. (1880-86). This collection of thousands of the briefest of proofs and with no material newer than 1860, aroused his genius. Having verified the results in carr's book, Ramanujan went beyond it, developing his own thousand ideas. In 1903 he Madras but lost the following University of Madras but lost the next years because he neglected all other studies in pursuit of mathematics.
Ramanujan continued his work without employment and lived in the poorest circumstances. After marrying in 1909 he began a search for permanent employment that culminated in an interview with a government official, Ramchandra Rao. Impressed by Ramanujan's mathematical powers. Rao supported his research for a time, but Ramanujan, unwilling to exist on charity, obtained a clerical post with the Madras Port Trust.
He died on April 26, 1920, in Kumbakonam.
Contribution to the field of Mathematics:
He was one of India's greatest mathematical geniuses. Using one of his identities, mathematicians have been able to calculate the value of `pi` correct to millions of places of decimal.
Indian mathematician whose contributions to the theory of numbers include pioneering discoveries of the properties of the partition function.
Ramanujan's knowledge of mathematics was starting. Although he was almost completely unaware of modern developments in mathematics his mastery of continued fractions was unequal to any living mathematician. He worked out the Riemann series, the elliptic integrals, the hypergeometric function, and his own theory of divergent series, in which he found a value for the sum of such series using a technique he invented that came to be called Ramanujan summation
It is worth mentioning here that the great Indian mathematician Srinivasa Ramanujan used very high levels of information to arrive at many of his statements, which he claimed were true. Many of these have turned out to be true and are well-known theorems. However, even to this day mathematicians all over the world are struggling to prove (or disprove) some of his claims(conjectures)
========X=======
Project No. 3
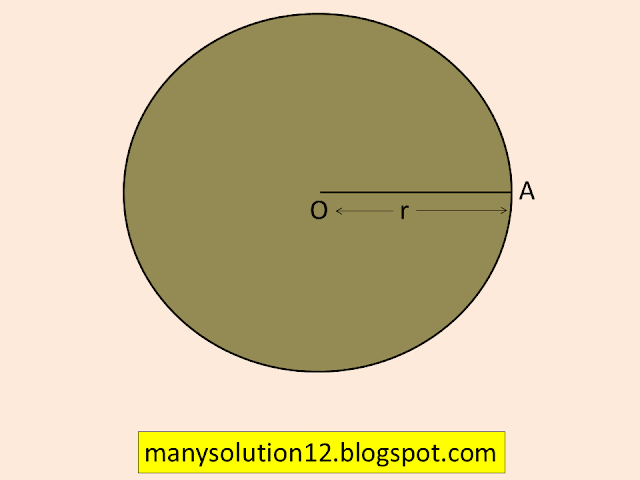
Objective: Review of perimeter and area of the circle with a diagram and example.
Perimeter (circumference):
The distance around the circle is called the Circumference of the Circle.
The Circumference of circle `2pir`
where
`pi=22/7,` `r` is the radius of the circle.
Example:
Find the perimeter of the circle of radius `7cm`.
Sol. :
Given:
The radius of the circle is `7 cm`
To find:
The perimeter of the circle.
Solve:
The perimeter of circle `2pir`
`=2times22/7times7`
`=2times22`
`=44 cm`
Answer:
The perimeter of the circle is `44cm`.
Area of the Circle
The area of the circle is the amount of space within the perimeter (circumference) of a two-dimensional shape.
The area of the circle `=pir^2`
The area of the circle's unit is `cm^2, m^2`.
where
`pi=22/7`, `r` is the radius of the circle.
Example:
Find the area of the circle of radius `7 cm`.
Sol. :
Given:
The radius of the circle `r=7cm`
To Find:
The area of the circle.
Solve:
The Area of the circle `=pir^2`
`=22/7times(7)^2`
`=22/7times7times7`
`=22times7`
`=154 cm^2`
Answer:
The area of the circle is `154 cm^2`.
========X=======
Project No. 4
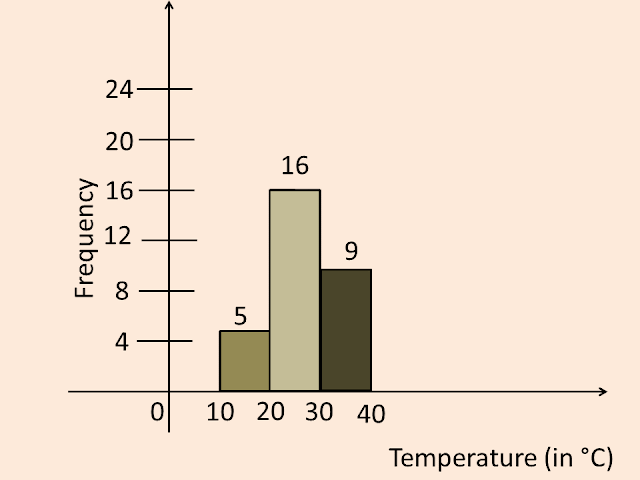
Objective: Presentation of 30 days recorded daily maximum temperature data in your city in the form of a graded frequency table and measurement of the mean of these data.
Daily maximum temperature
`27, 30, 25, 35, 17, 21, 27, 29, 31, 30,`
`19, 24, 23, 32, 30, 25, 18, 27, 24, 21,`
`35, 30, 27, 31, 19, 24, 17, 29, 27, 23.`
Graded frequency table
| ||
| ||
|
Measurement of the Mean of the data
Mean `overlineX=(∑f_itimesx_i)/(∑f_i)`
Mean `overlineX=790/30=26.66`
Answer:
Measurement of the Mean of the data `26.66^circC`.
========X=======
Project No. 5
Objective: `π` is the most mysterious number of the world.
Value of `pi`
Aryabhatt (476-550 A.D.) was the first mathematician who evaluated the approximate value of `π` i.e. the ratio of circumference to the diameter of a circle.
Add `4` in `100,` multiply by `8,` and add `62000` in the product. This is the approximate value of the circumference of the circle of diameter is `62832` approximately.
Pie `(π)` = (circumference)/(diameter) = `62832/20000`
Therefore according to Aryabhatt `π = 3.1416` which is true upto `4` places of decimal even todays.
`π/10 = 0.3141592653589793238462633832792`
Archimedes (in about 240 B.C.) obtained the value of π as `223/71` and `22/7` respectively on the basis of the perimeters of polygons inscribed and circumscribed in a unit circle, correct to two places of decimals as `3.14`. This is found in his books 'measure of a circle'. After this Klandius Ptolemi of Alexandria `(150 A.D.)` and Tus Chung-Chih of China worked on finding the value of π as the ratio of the circumference and diameter of a circle.
========X=======
Project No. 6
Objective: Geometric applications in daily life.
Geometry
A glance at the History of mathematics shows that geometry was studied in the early Vedic period also. The information about mathematics of that period is available in the form of the Shulv-Sutra (3000 B.C.) from Kalap named Vedang. The roap used in the measurement of altars is called Shulva. Shulva means 'presentation of information in the short form. The theorem commonly named as 'Pythagoras theorem', construction was explained in Shulva Sutras (Bodhayan Shulva Sutra) Shulva Sutra is known by the name of their creators like Bodhayan, Aapstambh, Katyayan, Manav, Maitrayan, etc. Some of these are (1) Garuvedi (2) Kurmvedi.
Some applications of Shulve Sutra Geometry are given below:
i) Construction of triangles, squares, rectangles, and other typical geometrical figures.
ii) Construction of geometrical figures whose area is the sum or difference of the area of some given figures.
iii) To construct a square from a circle and vice-versa.
Aryabhatt, Bhaskara first, Brahmgupt, and Mahavira have remarkable contributions to the field of geometry.
Aryabhata described geometry in various sections of his books. He mainly wrote the formulas of the area of triangles, quadrilaterals, circles, and volumes of solids.
In the 'Kshetra vyavhar' chapter of Bhaskaracharya's Leelawati, he described the areas of right triangles and quadrilaterals circles, and the surface area and volume of spheres.
The modern study of algebra started with definitions, axioms, propositions, and theorems described in the book 'Elements' written by Greek mathematician Euclid. In the work of 13 volumes, number principles and elementary algebra are also discussed with geometry. It is understood that Euclid developed this work in 323 B.C.
The word geometry is made up of two Greek words 'geo and metro'. Geo means 'the earth' and metron means 'to measure. Thus, the origin of geometry is as old as the development of human civilization, when human beings required the measurement of the land. Probably, Egyptians were the first to study geometry. Their main interest was in the problem of mensuration, as the area to find rectilinear figures like triangles and rectangles. After this Babylonian, evolved formulas for finding areas of different rectilinear figures. These formulas are found in the Babylonian book Rhind Papyrus (1650 B.C.). Egyptians and Babylonians both mostly used geometry for practical works and could not work for the development of geometry, But the presentation of geometry as systematic science is credited to Greeks.
========X=======
Project No. 7
Objective: Find out the HCF of 02 numbers experimentally on the basis of Euclid's division algorithm.
Euclid's division algorithm is a technique to compute the Highest Common Factor (HCF) of two given positive integers. Recall that the HCF of two positive integers a and b is the largest positive integer d that divides both a and b.
Let us see how the algorithm works, through an example first. Suppose we need to find the HCF of the 135 and 225. We start with the larger integer, that is 225 then we use Euclid's lemma to get
Examples:
Q1. Use Euclid's division algorithm to find the HCF of:
i) `135` and `225` ii) `196` and `38220` iii) `867` and `255`
Sol.
By Euclid's division algorithm
`text{a = bq + r}`
where
`text{a = 225,}`
`text{b =135,}`
`text{q = quotient and r = remainder}`
`225=135times1+90`
`135=90times1+45`
`90=45times2+0`
Answer:
The `text{HCF}` of `135` and `225` is `45`.
ii)
By Euclid's division algorithm
`text{a = bq + r}`
where
`text{a = 38220,}`
`text{b = 196,}`
`text{q = quotient and r = remainder}`
`38220 = 196times195 + 0`
Answer:
The `text{HCF}` of `196` and `38220` is `196`.
iii)
By Euclid's division algorithm
`text{a = bq + r}`
where
`text{a = 867,}`
`text{b = 225,}`
`text{q = quotient and r = remainder}`
`867=225times3+102`
`225=102times2+51`
`102=51times2+0`
Answer:
The `text{HCF}` of `867` and `225` is `51`.
========X=======
Project No. 8
Objective: To verify the consistent/inconsistent conditions of a pair of linear equations in two variables by graphical method.
A pair of linear equations that has no solution is called an`text{inconsistent}` pair of linear equations. A pair of linear equations in two variables, which has a solution, is called a `text{consistent}`
pair of linear equations. A pair of linear equations which are equivalent has infinitely many distinct common solutions. Such a pair is called a dependent pair of linear equations in two variables. Note that a dependent pair of linear equations is always consistent.
We can now summarise the behavior of lines representing a pair of linear equations in two variables and the existence of solutions as follows:
i) The lines may intersect at a single point. In this case, the pair of equations has a unique solution (consistent pair of equations).
ii) The lines may be parallel. In this case, the equations have no solution (inconsistent pair of equations).
iii) The lines may be coincident. In this case, the equations have infinitely many solutions [dependent(consistent) pair of equations].
Let us now go back to the pairs of linear equations formed in Examples 1, 2, and 3, and note down what kind of pair they are geometrical.
i) x-2y=0 and 3x+4y-20 =0 (The lines intersect)
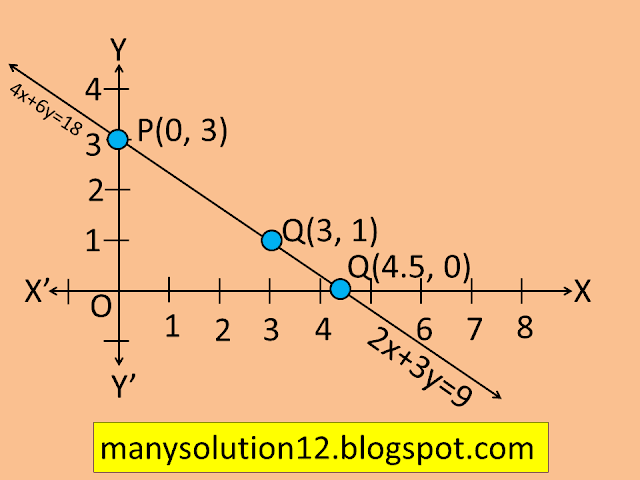
ii) 2x+3y-9=0 and 4x+6y-18=0 (The lines coincide)
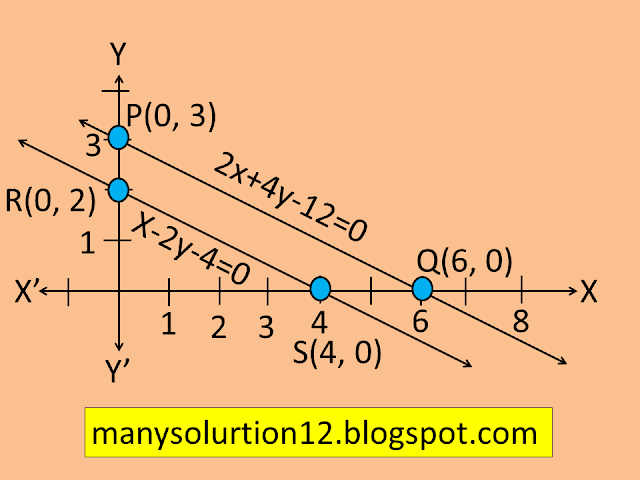
iii) x+2y-4=0 and 2x+4y-12=0 ( The lines are parallel)
Let us now go back to the pairs of linear equations formed in Examples 1, 2, and 3, and note down what kind of pair they are graphical.
i) x-2y=0 and 3x+4y-20 =0 (The lines intersect)
ii) 2x+3y-9=0 and 4x+6y-18=0 (The lines coincide)
iii) x+2y-4=0 and 2x+4y-12=0 ( The lines are parallel)
========X=======
Project No. 9
Objective: Verification of distance formula by graphical method.
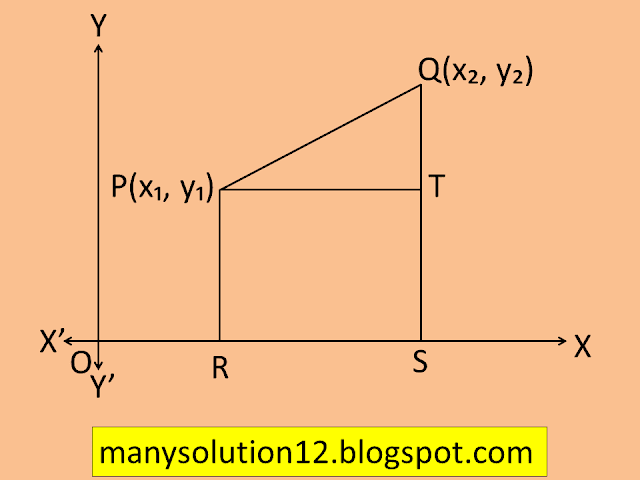
Let us now find the distance between any two points `text{P}(x_1, y_1)` and `text{Q}(x_2, y_2).` Draw `text{PR}` and `text{QS}` perpendicular to the x-axis. A perpendicular from the point `text{P}` on `text{QS}` is drawn to meet it at the point `text{T}`(see figure)
Then,
`text{OR} = x_1`,
`text{OS} = x_2`.
So,
`text{PR }= x_2-x_1 = text{ PT}`.
Also,
`text{SQ } = y_2`,
`text{ST = PR }= y_1`.
So,
`text{QT = } y_2-y_1`.
Now, applying the Pythagoras theorem in `triangle text{ PTQ}`, we get
`text{PQ}^2 = text{PT}^2 + text{QT}^2`
`= (x_2-x_1)^2+(y_2-y_1)^2`
Therefore,
`text{PQ } = sqrt( (x_2-x_1)^2+(y_2-y_1)^2)`,
Note that since the distance is always non-negative, we take only the positive square root. So, the distance between the points `text{P}(x_1, y_1)` and `text{Q}(x_2, y_2)` is
`text{PQ } = sqrt( (x_2-x_1)^2+(y_2-y_1)^2)`,
which is called the `text{distance formula.}`
`text{Remarks:}`
1. In particular, the distance of a point `text{P}(x, y)` from the origin `text{O}(0, 0)` is given by `text{OP }=sqrt(x^2 + y^2)`
2. We can also write, `text{PQ } = sqrt( (x_2-x_1)^2+(y_2-y_1)^2)`.
Examples:
Q1. Find the distance between the following points:
i) `(2, 3), (4,1)`
ii) `(-5,7), (-1, 3)`
iii) `(a, b), (-a, -b)`
Sol. :
i)
Given:
Let `P(2, 3), Q(4, 1)`
Solve:
Distance `=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`
`PQ=sqrt((4-2)^2+(1-3)^2)`
`PQ=sqrt((2)^2+(-2)^2)`
`PQ=sqrt(4+4)`
`PQ=sqrt8`
`PQ=2sqrt2` units.
Answer:
Distance `2sqrt2` units.
ii)
Given:
Let `P(-5, 7), Q(-1, 3)`
Solve:
Distance `=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`
`PQ=sqrt((-1+5)^2+(3-7)^2)`
`PQ=sqrt((4)^2+(-4)^2)`
`PQ=sqrt(16+16)`
`PQ=sqrt(32)`
`PQ=16sqrt2` units
Answer:
Distance `16sqrt2` units.
iii)
Given:
Let `P(a, b), Q(-a, -b)`
Solve:
Distance `=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`
`PQ=sqrt((-a-a)^2+(-b-b)^2)`
`PQ=sqrt((-2a)^2+(-2b)^2)`
`PQ=sqrt(4a^2+4b^2)`
`PQ=sqrt(4(a^2+b^2))`
`PQ=2sqrt(a^2+b^2)` units
Answer:
Distance `2sqrt(a^2+b^2)` units.
========X=======
Project No. 10
Objective: To find the sum of the first n natural numbers.
We will find the sum of the first `n` terms of an`text{ AP}:`
`text{a, a+d, a+2d,.......}`
The `text{nth}` term of this `text{AP}` is `text{a+(n-1)d}`. Let `text{S}` denote the sum of the first `text{ n}` terms of the `text{AP}`. We have
`text{S = a+(a+d)+(a+2d)+...+[a+(n-1)d]}`___(1)
Rewriting the terms in reverse order, we have
`text{S = [a+(n-1)d]+[a+(n-2)d]+....+(a+d)+a}`___(2)
On adding (1) and (2), term-wise. we get
`text{2S =}``(text{[2a+(n-1)d]+[2a+(n-1)d]+...+[2a+(n-1)d]})/(ntext{terms})`
or,
`text{2S = }``text{n[2a+(n-1)d]}` (since, there are n terms)
or,
`text{S= }``(text{n})/2text{[2a+(n-1)d]}`
So, the sum of the first n terms of an AP is given by
`text{S= }``(text{n})/2text{[2a+(n-1)d]}`
We can also write this as
`text{S= }``(text{n})/2text{[a+a+(n-1)d]}`
i.e.,
`text{S= }``(text{n})/2text{(a+a}_n)`_____(3)
Now, if there are only `n` terms in an `text{AP},` then `text{a}_n =l`, the last term.
From (3), we see that
`text{S= }``(text{n})/2text{(a+}l)`_____(4)
This form of the result is useful when the first and the last terms of an `text{AP}` are given and the common difference is not given.
Example:
1) To find the sum of the first n natural numbers.
Sol.
We will now use the same technique to find the sum of the first `n` natural numbers of an`text{ AP}:`
`text{a, a+d, a+2d,.......}`
The `text{nth}` term of this `text{AP}` is `text{a+(n-1)d}`. Let `text{S}_n` denote the sum of the first `text{ n}` natural numbers of the `text{AP}`. We have
`text{S}_n ``text{ = a+(a+d)+(a+2d)+...+[a+(n-1)d]}`___(1)
Rewriting the terms in reverse order, we have
`text{S}_n``text{ = [a+(n-1)d]+[a+(n-2)d]+....+(a+d)+a}`___(2)
On adding (1) and (2), term-wise. we get
`text{2S}_n =``(text{[2a+(n-1)d]+[2a+(n-1)d]+...+[2a+(n-1)d]})/(text{n natural numbers})`
or,
`text{2S}_n =``text{n[2a+(n-1)d]}`
or,
`text{S}_n= ``(text{n})/2text{[2a+(n-1)d]}`
So, the sum of the first n natural numbers of an AP is given by
`text{S}_n= ``(text{n})/2text{[2a+(n-1)d]}`
========X=======
Project No. 11.
Objective: Explain the surface area of a combination of solids with two examples.
Surface Area of a Combination of Solids
In our day-to-day life, we come across solids made up of combinations of two or more of the basic solids as shown in examples.
Now, whenever we come across a new problem, we first try to see, if we can break it down into smaller problems, we have earlier solved. We can see that this solid is made up of a cylinder with two hemispheres stuck at either end. It looks like what we have in example 1, after we put the pieces all together.
Example 1.
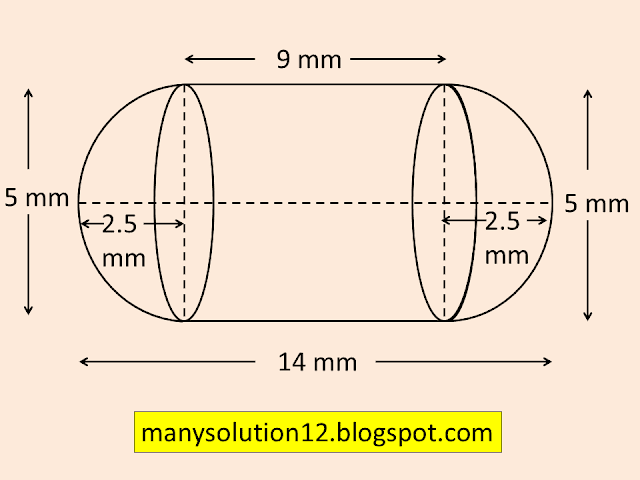
A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (see figure). The length of the entire capsule is `text{14 mm}` and the diameter of the capsule is `text{5 mm}`. Find its surface area.
`text{Sol. :}`
`text{Given :}`
`text{Length of the entire capsule is 14 mm}`
`text{Diamter of hemisphere & cylinder }d = 5 text{mm}`
`text{Radius of hemisphere & cylinder }r = 5/2 text{mm}`
`text{To find :}`
`text{Surface Area of the capsule}`.
`text{Solve :}`
`text{Lenght of the capsule = }``text{length of the cylinder }(l)``text{+ 2}times text{radius of the hemisphere}`
`14 = l + 5`
`l = 14 - 5`
`l = 9`
`text{S A of capsule = C S A Cylinder }`
`text{ + 2 (C S A of hemisphere)}`
`text{S A of capsule} = 2pirl + 2 times 2pir^2`
`text{S A of capsule} = 2pir(l + 2r)`
`text{S A of capsule} = 2times22/7times5/2(9 + 2times5/2)`
`text{S A of capsule} = 110/7(14)`
`text{S A of capsule} = 220 text{ mm}^2`
`text{Answer :}`
`text{S A of the capsule is 220 mm}^2`.
Example 2.
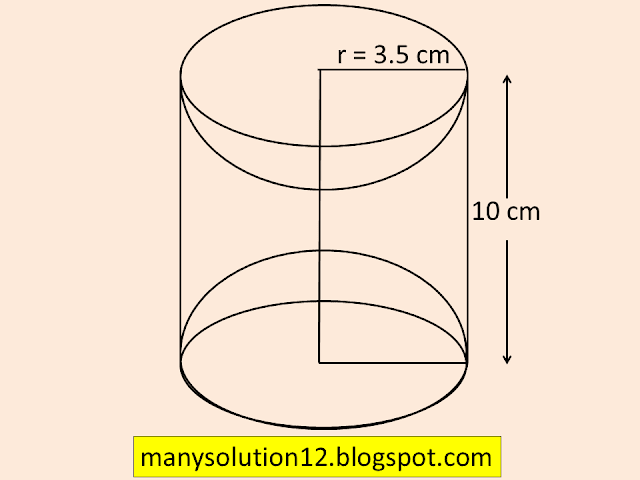
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Figure. If the height of the cylinder is `text{10 cm}`, and its base is of radius `text{3.5 cm,}` find the total surface area of the article.
`text{Sol. :}`
`text{Height of the Cylinder } h = 10 text{ cm}`
`text{Radius of the base} r = 3.5 text{ cm}`
`text{To find :}`
`text{The total surface area of the article}`
`text{Solve :}`
`text{T S A of the article = C S A of Cylinder}`
`text{ + 2(C S A of hemisphere)}`
`text{ = }2pirh + 2times2pir^2`
`text{ = }2pir(h + 2r)`
`text{ = }2times22/7times3.5(10 + 2times3.5)`
`text{ = }22 times 17`
`text{ = }374 text{cm}^2`
`text{Answer :}`
`text{T S A of the article is 374 cm}^2`.
see more click (Ex 13.1)
Project No. 12.
Establish the trigonometric identities and use these identities to express the trigonometric ratios in terms of other trigonometric ratios.
Trigonometric Identities
An equation is called an identity when it is true for all values of the variables involved. Similarly, an equation involving trigonometric ratios of an angle is called a trigonometric identity, if it is true for all values of the angles(s) involved.
In this section, we will prove one trigonometric identity, and use it further to prove other useful trigonometric identities.
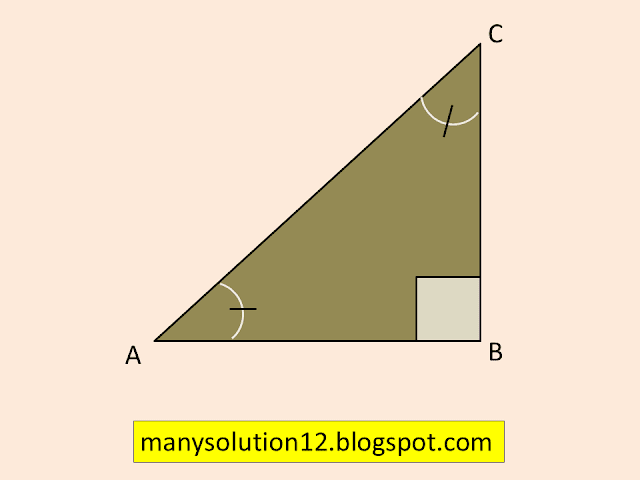
In `triangle text{ ABC}` right-angled at `text{B}` see figure,
By Pythagoras theorem
`text{(AB)}^2 + text{(BC)}^2 = text{(AC)}^2`___(1)
`text{Dividing both sides (1) by (AC)}^2`
`(AB)^2/(AC)^2 + (BC)^2/(AC)^2 = (AC)^2/(AC)^2`
`((AB)/(AC))^2 + ((BC)/(AC))^2 = ((AC)/(AC))^2`
`(cos A)^2 + (sin A)^2 = 1`
`cos^2A +sin^2A = 1`_____(2)
This is true for all `text{A}` such that `0^circ le text{A} le 90^circ`. So, this is a trigonometric identity.
`text{Dividing both sides (1) by (AB)}^2`
`(AB)^2/(AB)^2 + (BC)^2/(AB)^2 = (AC)^2/(AB)^2`
`((AB)/(AB))^2 + ((BC)/(AB))^2 = ((AC)/(AB))^2`
`1 + tan^2A = sec^2A`_____(3)
This is true for all `text{A}` such that `0^circ le text{A} le 90^circ`. So, this is a trigonometric identity.
`text{Dividing both sides (1) by (BC)}^2`
`(AB)^2/(BC)^2 + (BC)^2/(BC)^2 = (AC)^2/(BC)^2`
`((AB)/(BC))^2 + ((BC)/(BC))^2 = ((AC)/(BC))^2`
`cot^2A + 1 = cosec^2A`_____(4)
This is true for all `text{A}` such that `0^circ le text{A} le 90^circ`. So, this is a trigonometric identity.
Using these identities, we can express each trigonometric ratio in terms of other trigonometric ratios, i. e., if any one of the ratios is known, we can also determine the values of other trigonometric ratios.
Example 1.
Express the trigonometric ratios `sin A, sec A` and `tan A` in terms of `cot A`.
Sol. :
`sin A = 1/(cosec A) = 1/(sqrt (cosec^2 A))`` = 1/sqrt(1 + cot^2 A)`
`sec A = 1/(cos A) = (1/sin A)/(cos A/sin A) = (cosec A)/(cot A)`
`sec A = sqrt(cosec^2 A)/(Cot A) = sqrt(1 + cot^2 A)/cot A`
`tan A = 1/cot A`
Answer:
`sin A = 1/sqrt(1 + cot^2 A)`, `sec A = sqrt(1 + cot^2 A)/cot A` and `tan A = 1/cot A`
Example 2.
Write all the other trigonometric ratios of `angle A` in terms of `sec A`.
Sol. :
Let `triangle ABC` is right-angled at `angle B` and `sec A = x`
`sec A = x = (AC)/(AB)`
By Pythagoras theorem
`BC^2 = AC^2 - AB^2`
`BC^2 = x^2 - 1`
`BC = sqrt(x^2 -1)`
`sin A = (BC)/(AC) = sqrt(x^2 - 1)/x = sqrt(sec^2 - 1)/(sec A)`
`cos A = (AB)/(AC) = 1/x = 1/sec A`
`tan A = (BC)/(AB) = sqrt(x^2 - 1)/1 = sqrt(sec^2 A - 1)`
`cosec A = (AC)/(BC) = x/sqrt(x^2 - 1) = (sec A)/sqrt(sec A - 1)`
`cot A = (AB)/(BC) = 1/sqrt(x^2 - 1) = 1/sqrt(sec^2 A - 1)`
Answer:
`sin A = sqrt(sec^2 - 1)/(sec A)`
`cos A = 1/sec A`
`tan A = sqrt(sec^2 A - 1)`
`cosec A = (sec A)/sqrt(secA - 1)`
`cot A = 1/sqrt(sec^2 A - 1)`
=========X========
Project No. 13.
Explain the volume of a combination of solids with two examples.
The volume of a Combination of Solids
Here, we shall see how to calculate the volume of solids. It may note that in calculating the surface area we have not added the surface areas of the two constituents, because some parts of the surface area disappeared in the process of joining them. However, this will not be the case when we calculate the volume. The volume of the solid formed by joining two basic solids will actually be the sum of the volumes of the constituents as we see in the examples below.
Example 1.
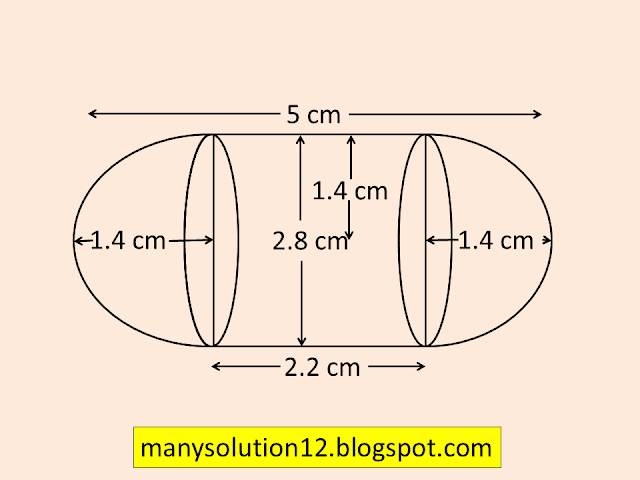
A gulab jamun contains sugar syrup up to about `30%` of its volume. Find approximately how much syrup would be found in `45` gulab jamuns, each shaped like a cylinder with two hemispherical ends with length `text{5 cm}` and diameter `text{2.8 cm}`(see Figure).
`text{Sol. :}`
`text{Diameter of hemisphere & Cylinder }``d = 2.8text{ cm}`
`text{Radius of hemisphere & Cylinder }``r = 1.4text{ cm}`
`text{Length of Cylinder }h = 5 - 2(1.4)`` = 2.2text{ cm}`
`text{To find :}`
`text{Volume of syrup}`.
`text{Solve :}`
`text{Volume of a gulab jamun = }``{Volume of Cylinder}``text{+ 2Volume of hemishere}`
`text{V} = pir^2h + 2times2/3pir^3`
`text{ } = pir^2(h + 2times2/3r)`
`text{ } = 22/7times(1.4)^2(2.2 + 2times2/3times1.4)`
`text{ } = 22/7times1.4times1.4(2.2 + (4times1.4)/3)`
`text{ } = 22times1.4times0.2((6.6 + 5.6)/3)`
`text{ } = 22times0.28times(12.2)/3`
`text{ } = 6.16times12.2/3`
`text{ } = 75.152/3`
`text{Total Vol. of 45 gulab jamun} = 45 times 75.152/3`
`text{ } = 15times75.152`
`text{ } = 1127.28text{cm}^3`
`text{Volume of syrup} = 30% times text{Total Volume}`
`text{ } = 30/100 times 1127.28`
`text{ } = 338.184text{cm}^3`
`text{Answer :}`
`text{Volume of syrup 338.184 cm}^3`.
Example 2.
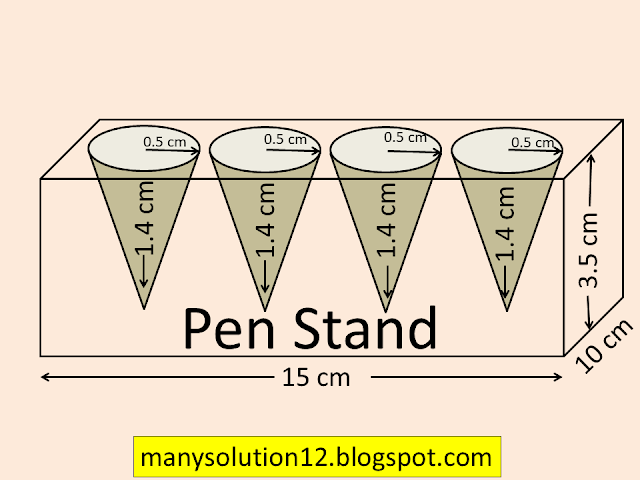
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are `text{15 cm by 10 cm by 3.5 cm.}` The radius of each of the depressions is `text{0.5 cm}` and the depth is `text{1.4 cm}`. Find the volume of wood in the entire stand (see figure).
`text{Sol. :}`
`text{Given :}`
`text{Dimensions of the cuboid 15 cm, 10 cm, }``text{3.5 cm}`
`text{Radius of depressions }r =0.5text{ cm}`
`text{Depth of depressions }h = 1.4text{ cm}`
`text{To find :}`
`text{The volume of wood in the entire stand.}`
`text{Solve :}`
`text{Volume of wood = }``text{Vol. of cuboid}``text{- Vol. of 4 conical dipression}`
`text{V} = LtimesBtimesH - 4times1/3pir^2h`
`text{} = 15times10times3.5 - 4times1/3times22/7times``(0.5)^2times1.4`
`text{} = 525 - 4times1/3times22times0.25times0.2`
`text{} = 525 - 1.47`
`text{} = 523.53text{cm}^3`
`text{Answer :}`
`text{The Volume of wood 523.53 cm}^3.`
See more click (Ex 13.2)
======X=======
Project No. 14.
Explain the conversion of solid from one shape to Another with two examples.
Generally, candles are in the shape of cylinders. You may have also seen some candles shaped like an animal.
How are they made? If you want a candle of any special shape, you will have to heat the wax in a metal container till it becomes completely liquid. Then you will have to pour it into another container that has the special shape that you want. For example, take a candle in the shape of a solid cylinder, melt it and pour the whole of the molten wax into another container shaped like a rabbit. On cooling, you will obtain a candle in the shape of a rabbit. The volume of the new candle will be the same as the volume of the earlier candle.
Let us consider some examples.
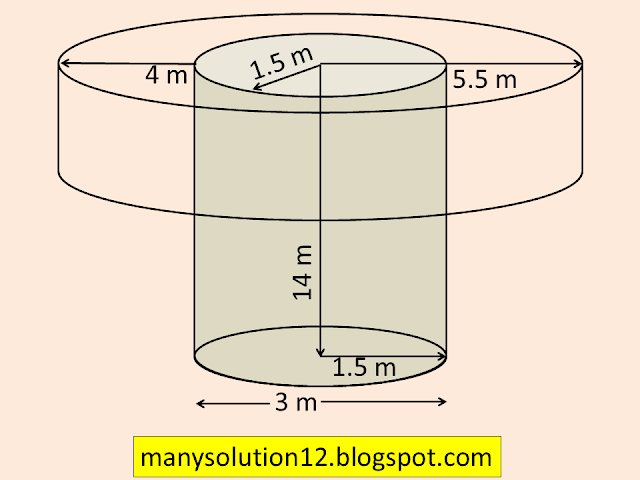
Example 1.
A well of diameter `text{3 m}` is dug `text{14 m}` deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width `text{4 m}` to form an embankment. Find the height of the embankment.
`text{Sol. :}`
`text{Given :}`
`text{Diameter of well (cylinder) }d = 3text{ m}`
`text{Radius of well (cylinder) }r_1 = 3/2 = 1.5 text{ m}`
`text{Depth (height) of well (cylinder) }h = 14text{ m}`
`text{Width of embankment} = 4text{m }`
`text{Radius of big circle }r_2 = 4 + 1.5 = 5.5text{ m}`
`text{To find :}`
`text{The height of the embankment.}`
`text{Solve :}`
`text{height of the embankment} = x`
`text{According to question}`
`text{Volume of embankment = Volume of well}`
`pi(r_2^2 - r_1^2)x = pir_1^2h`
`[(5.5)^2 - (1.5)^2]x = (1.5)^2times14`
`[(5.5+1.5)(5.5 - 1.5)]x = 2.25times14`
`[7times4]x = 2.25times14`
`x = (2.25times14)/(7times4)`
`x = 1.125 text{ m}`
`text{Answer :}`
`text{The height of the embankment 1.125 m.}`
Example 2.
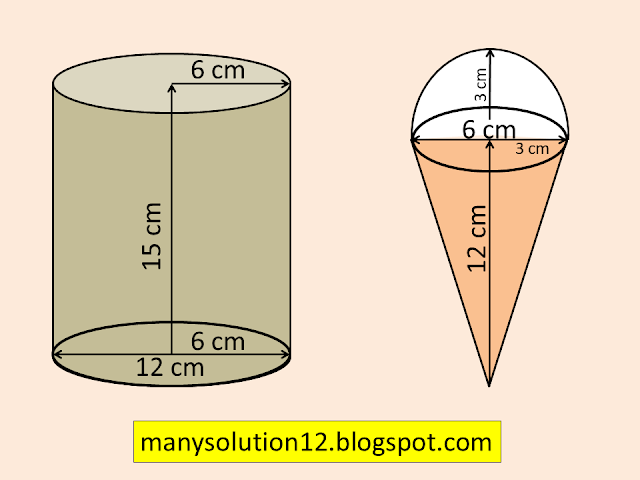
A container shaped like a right circular cylinder having a diameter `text{12 cm}` and a height `text{15 cm}` is full of ice cream. The ice cream is to be filled into cones of height `text{12 cm}` and diameter `text{6 cm},` having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
`text{Sol. :}`
`text{Given :}`
`text{Diameter of Cylinder }d = 12text{ cm}`
`text{Radius of Cylinder }r = 6text{ cm}`
`text{Height of Cylinder }h =15text{ cm}`
`text{Hight of Cone }h' = 12text{ cm}`
`text{Diameter of Cone }d' = 6text{ cm}`
`text{Radius of Cone & hemisphere }r' = 3text{ cm}`
`text{To find :}`
`text{The of ice-cream cones.}`
`text{Solve :}`
`text{According to question}`
`text{Volume of ice-cream Cylinder}= pir^2h`
`text{V}_1 = pi(6)^(2)15`
`text{V}_1 = 540pi`
`text{Vol. of ice-cream cone = Vol. of cone}`
`text{ + Vol. of hemisphere}`
`text{V}_2 = 1/3pi(r')^2h' + 2/3pi(r')^3`
`text{ } = (pi(r')^2)/3(h' + 2r')`
`text{ } = (pi(3)^2)/3(12+2times3)`
`text{ } = 3times18pi`
`text{ } = 54pi`
`text{ Number of ice-cream cones }= V_1/V_2`
`text{ Number of ice-cream cones }= (540pi)/(54pi)`
`text{ = }10`
`text{Answer :}`
`text{The number of ice-cream cones 10.}`
See more click (Ex 13.3)
======X=========
Project No. 15.
Explain the Mean of Grouped Data by Step deviation method.
The mean or average of observations, as we know, is the sum of the value of all the observations divided by the total number of observations. We can write mean in short `overlinex`.
Here, we discuss the mean of grouped data by step deviation method.
We note that:
1. The step-deviation method will be convenient to apply if all the `d_i`'s have a common factor.
2. The mean obtained by all three methods is the same.
3. The assumed mean method and step-deviation method are just simplified forms of the direct method.
4. The formula `overline x = a + h overline u` still holds if `a` and `h` are not as given above, but are any non-zero numbers such that `u_i = (x_i - a)/h`.
Let us apply this method.
Example 1.
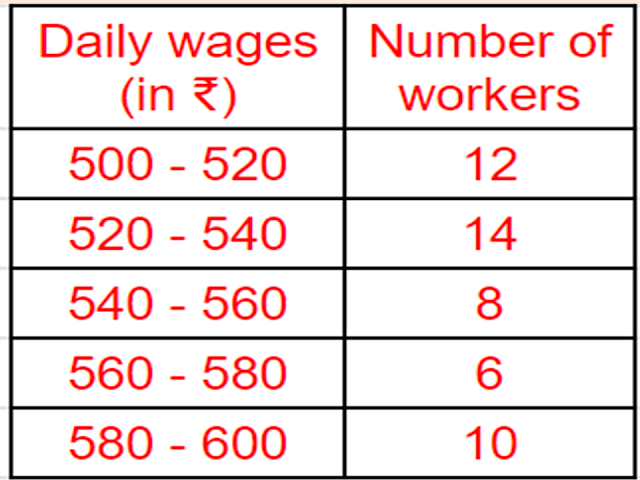
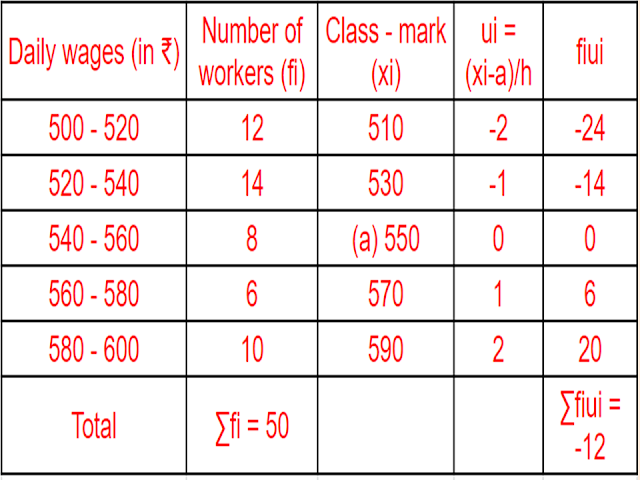
Consider the following distribution of daily wages of `50` workers of a factory
Find the mean daily wages of the workers of the factory by using an appropriate method.
Sol. :
`text{Mean }overlinex = a + (∑f_iu_i)/(∑f_i)timesh`
`= 550+(-12times20)/50`
`= 550-240/50`
`=550-4.80`
`= 545.20`
`text{Answer:}`
`₹ 545.20.`
Example 2.
Thirty women were examined in a hospital by a doctor and the number of heartbeats per minute were recorded and summarised as follows. Find the mean heartbeats per minute for these women, choosing a suitable method.
`text{Mean }overlinex = a+(∑f_iu_i)/(∑f_i) times h`
`overline x =75.5+(4 times 3)/30`
`overline x = 75.5 + 0.4`
`overline x = 75.9`
`text{Answer:}`
`overline x =75.9`
======X=========
Project No. 16.
Explain the Mode of Grouped Data with two examples.
Mode: A mode is that value among the observations which occurs most often, that is, the value of the observation having a maximum frequency. Further, we discussed finding the mode of ungrouped data. Here, we shall discuss ways of obtaining a mode of grouped data. It is possible that more than one value may have the same maximum frequency. In such situations, the data is said to be multimodal. Though grouped data can also be multimodal, we shall restrict ourselves to problems having a single mode only.
In a grouped frequency distribution, it is not determined the mode by looking at the frequencies. Here, we can only locate a class with the maximum frequency, called the modal class. The mode is a value inside the modal class.
Let us consider the following examples,
Example 1.
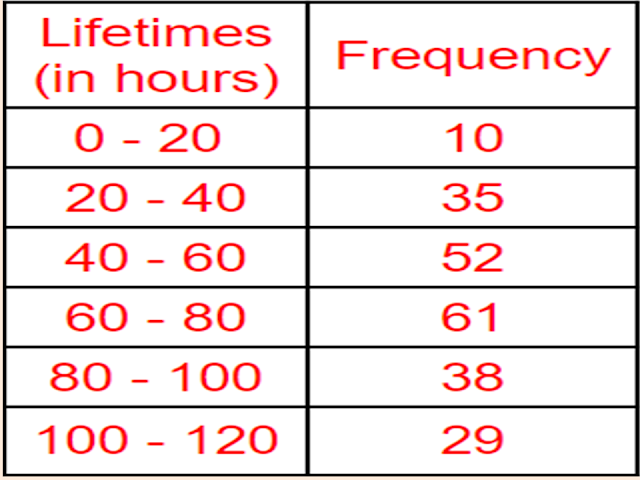
The following data gives the information on the observed lifetimes (in hours) of `225` electrical components:
Determine the modal lifetimes of the components.
Sol. :
`text{For Mode}`
`text{maximum class frequency is 61}`
`text{modal class = 60—80}`
`text{lower limit l = 60}`
`text{class size h = 20}`
`text{frequency of modal class}` `f_1 = 61`
`text{frequency just before modal class}` `f_0 = 52`
`text{frequency just after modal class}` `f_2 = 38`
`text{Mode Z}` `= l + ((f_1 - f_0)/(2f_1-f_0-f_2))``times text{ h}`
`text{Mode Z}` `= 60 + ((61 - 52)/(2 times 61 - 52 - 38)) times 20`
`text{Mode Z}` `= 60 + ((9)/(122-90)) times 20`
`text{Mode Z}` `= 60 + (180)/(32)`
`text{Mode Z}` `= 60 + 5.63`
`text{Mode Z}` `= 65.63`
`text{Answer:}`
`text{Mode = 65.625 hours.}`
Example 2.
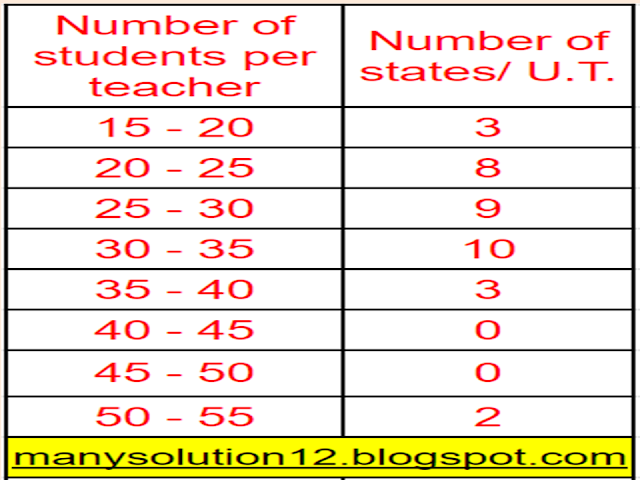
The following distribution gives the state-wise teacher-student ratio in higher secondary schools in India. Find the mode and mean of this data. Interpret the two measures.
Sol. :
`text{For Mode}`
`text{maximum class frequency is 10}`
`text{modal class = 30—35}`
`text{lower limit l = 30}`
`text{class size h = 5}`
`text{frequency of modal class}` `f_1 = 10`
`text{frequency just before modal class}` `f_0 = 9`
`text{frequency just after modal class}` `f_2 = 3`
`text{Mode Z}` `= l + ((f_1 - f_0)/(2f_1-f_0-f_2))``times text{ h}`
`text{Mode Z}` `= 30 + ((10 - 9)/(2 times 10 - 9 - 3)) times 5`
`text{Mode Z}` `= 30 + ((1)/(20-12)) times 5`
`text{Mode Z}` `= 30 + (5)/(8)`
`text{Mode Z}` `= 30 + 0.625`
`text{Mode Z}` `= 30.625`
`text{Answer:}`
`text{Mode Z}` `= 30.625`
======X=======
Project No. 17.
Explain the Median of Grouped Data with two examples.
The median is a measure of central tendency which gives the value of the middle-most observation in the data. Recall that for finding the median of ungrouped data, we first arrange the data values of the observations in ascending order. Then, if `n` is odd, the median is the `((n+1)/2)`th observation. And, if `n` is even, then the median will be the average of the `n/2`th and the `(n/2 +1)`th observations.
Let us see how to obtain the median of grouped data, through the following examples,
Example 1.
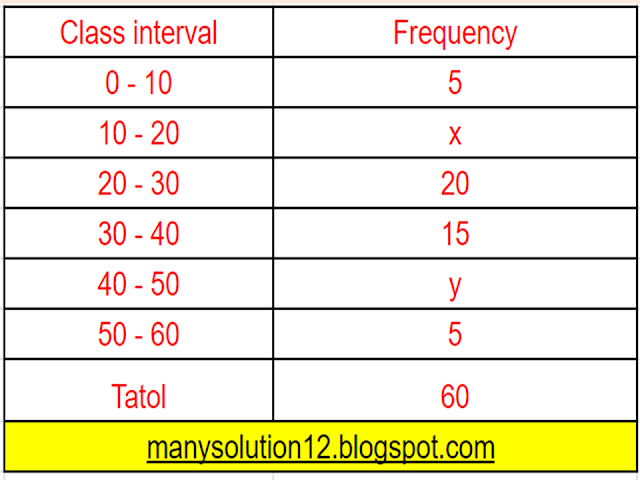
If the median of the distribution given below is `28.5`, find the value of `x` and `y`.
Sol. :
`45 + x + y = 60`
`x + y = 60 - 45`
`x + y = 15`________(1)
`text{Median} = 28.5`
`text{Medain class} = (20 - 30)`
`text{lower limit } l = 20`
`text{Frequency } f = 20`
`text{Cumulative frequency } cf = 5 + x`
`text{class size} h = 10`
`n = 60`
`text{Median}` `= l + ((n/2 - cf)/(f)) times h`
`28.5 = 20 + ((60/2 - (5 + x))/(20)) times 10`
`57 = 40 + 30 - 5 - x`
`57 = 40 + 25 - x`
`57 = 65 - x`
`x = 65 - 57`
`x = 8`_________(2)
`8 + y = 15` [ from eq. (1) and (2)]
`y = 15 - 8`
`y = 7`
`text{Answer:}`
`text{value of x = 8 and y = 7}.`
Example 2.
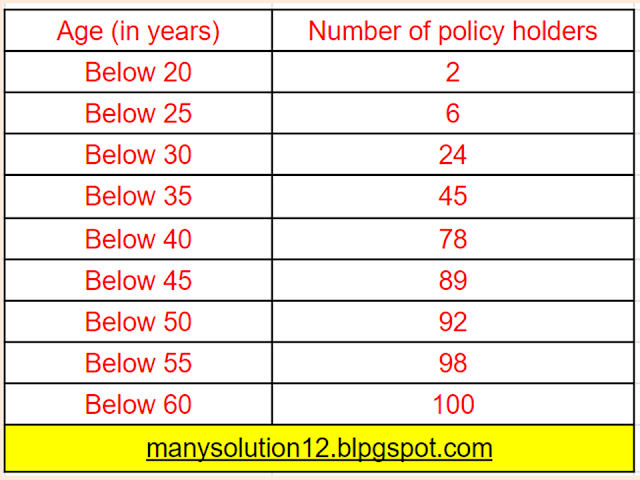
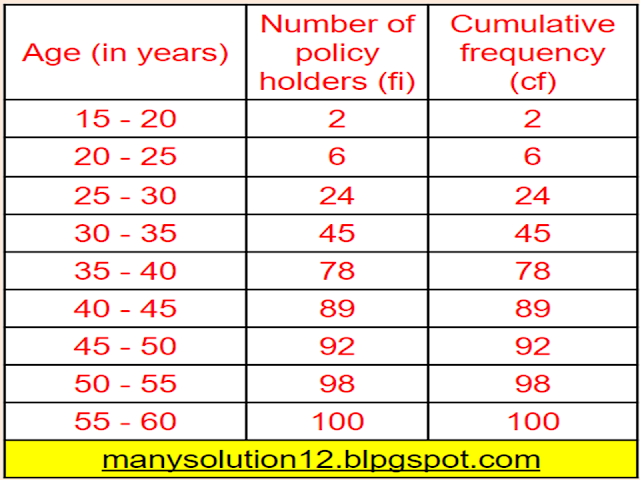
A life insurance agent found the distribution of ages of `100` policyholders. Calculate the median age, if policies are given only to persons having age `18` years onwards but less than `60` years.
Sol. :
`text{Median} = n/2 = 100/2 = 50^text(th) text{ term}`
`text{median class} = (35 - 40)`
`text{lower limit } l = 35`
`text{Cumulative frequency } cf = 45`
`text{Frequency } f = 33`
`text{class size } h = 40 - 35 = 5`
`text{Median}``= l + ((n/2 - cf)/f) times h`
`text{Median}``= 35 + ((50 - 45)/33) times 5`
`text{Median}``= 35 + (5times5)/33`
`text{Median}``= 35 + 25/33`
`text{Median}``= 35 + 0.76 = 35.76`
`text{Answer:}`
`text{Median age = 35.76 years`.
=====X========
Project No. 18.
Describe the Arithmetic Progressions with the help of examples.
An arithmetic progression is a list of numbers in which each term is obtained by adding a fixed number to the preceding term except the first term.
This fixed number is called the common difference of the AP. Remember that it can be positive, negative, or zero.
The general form of an AP.
`text{a, a + d, a + 2d, a + 3d,...}`
where `a` is the first term and `d` is the common difference.
Example 1.
Which of the following are APs? If they form an AP, find the common difference `d` and write three more terms.
`sqrt2, sqrt8, sqrt18, sqrt32,`..
`sqrt2, sqrt8, sqrt18, sqrt32,`..
`a_2-a_1=2sqrt2-sqrt2=sqrt2`
`a_3-a_2=3sqrt2-2sqrt2=sqrt2`
`a_4-a_3=4sqrt2-3sqrt2=sqrt2`......
`(a_2-a_1)=(a_3-a_2)=(a_4-a_3)``=...sqrt2=d`
Next three terms
`sqrt(32)+sqrt2=4sqrt2+sqrt2=5sqrt2=sqrt(50)`
`sqrt(50)+sqrt2=5sqrt2+sqrt2=6sqrt2=sqrt(72)`
`sqrt(72)+sqrt2=6sqrt2+sqrt2=7sqrt2=sqrt(98)`
Answer :
Yes, `d=sqrt2`, Next three terms `sqrt(50), sqrt(72), sqrt(98)`.
Example 2.
`sqrt3, sqrt6, sqrt9, sqrt17,`...
`sqrt3, sqrt6, sqrt9, sqrt17,`...
`a_2-a_1=sqrt6-sqrt3=sqrt3(sqrt2-1)`
`a_3-a_2=sqrt9-sqrt6=sqrt3(sqrt3-sqrt2)`
`a_4-a_3=sqrt(12)-sqrt9=sqrt3(2-sqrt3)`......
`(a_2-a_1)ne(a_3-a_2)ne(a_4-a_3)ne...`
Answer :
No.
======X=======
Project No. 19.
Establish the Relationship between Zeroes and Coefficients of Polynomials and give two examples.
In general, if `alpha` and `beta` are the zeroes of the quadratic polynomial `p(x) =ax^2 + bx + c, a ne 0,`
then you know that `x - alpha` and `x - beta` are the factors of `p(x)`. Therefore,
`ax^2 + bx + c = k(x - alpha)(x - beta)`, where `k` is a constant
`= k{x' -(alpha + beta)x +alpha beta]`
`= kx' - k(alpha + beta)x + k alpha beta`
Comparing the coefficients of `x^2, x` and constant terms on both sides, we get
`a = k, b = - k(alpha + beta)` and `c = k alpha beta`.
`alpha + beta = -b/a,`
`alpha beta = c/a`
Let us consider examples.
Examples 1.
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
i) `x^2-2x-8` ii) `4s^2-4s+1`
Sol. :
i) Given quadratic equation `x^2-2x-8` compare with `ax^2+bx+c=0`
where `a=1, b=-2` and `c=-8`
Let
`x^2-2x-8=0`
`x^2-4x+2x-8=0`
`x(x-4)+2(x-4)=0`
`(x-4)(x+2)=0`
`x-4=0`
`x=4`
`x+2=0`
`x=-2`
Now, the sum of the zeroes`=4-2=2`
`alpha+beta=-b/a=-((-2)/1)=2`
and the product of the zeroes`=4(-2)=-8`
`alpha times beta=c/a=-8/1`
Answer :
The required zeroes `4` or `-2` and the relation of zeroes & coefficient are verified.
ii) Given quadratic equation `4s^2-4s+1` compare with `ax^2+bx+c=0`
where `a=4, b=-4` and `c=-1`
Let
`4s^2-4s+1=0`
`4s^2-2s-2s+1=0`
`2s(2s-1)-1(2s-1)=0`
`(2s-1)(2s-1)=0`
`2s-1=0`
`s=1/2`
`2s-1=0`
`s=1/2`
Now, the sum of the zeroes`=1/2+1/2=1`
`alpha+beta=-b/a=-(4/-4)=1`
and the product of the zeroes`=1/2times1/2=1/4`
`alpha times beta=c/a=1/4`
Answer :
The required zeroes `1/4, 1/4` and the relation of zeroes & coefficient are verified.
======X============
Project No. 20.
Describe the nth term of an AP with the help of two examples.
The `n`th term `a_n` of the AP with first term `a` and common difference `d` is given by
`a_n = a + (n - 1)d`
`a_n` is also called the general term of the AP. If there are `m` terms in the AP, then `a_n` represents the last term which is sometimes also denoted by `l`.
Let us consider examples.
Example 1.
How many multiples of `4` lie between `10` and `250`?
Sol. :
AP is `12, 16, 20, 24, .....248`
where `a=12, d=4,` and `a_n=248`
`a_n=a+(n-1)d`
`248=12+(n-1)4`
`248=12+4n-4`
`248=8+4n`
`4n=248-8`
`4n=240`
`n=240/4`
`n=60`
Answer :
`n=60`.
Example 2.
The sum of the `4`th and `8`th terms of an AP is `24` and the sum of the `6`th and `10`th term is `44`. Find the first three terms of the AP.
Sol. :
Let the AP is `a, a+d, a+2d, ......`
According to question
`a_4+a_8=24`
`a+(4-1)d+a+(8-1)d=24`
`a+3d+a+7d=24`
`2a+10d=24`
`a+5d=12`______________(1)
and
`a_6+a_10=44`
`a+(6-1)d+a+(10-1)d=44`
`a+5d+a+9d=44`
`2a+14d=44`
`a+7d=22`_____________(2)
By equation (2) - (1)
`a+7d-(a+5d)=22-12`
`a+7d-a-5d=10`
`2d=10`
`d=10/2`
`d=5`
Put in equation (1)
`a+5(5)=12`
`a+25=12`
`a=-13`
`a_2=-13+(2-1)5=-13+5=-8`
`a_3=-13+(3-1)5=-13+10=-3`
`text{Answer:}`
`a_2 = -8,`
`a_3 = -3`.
======X==========






Comments