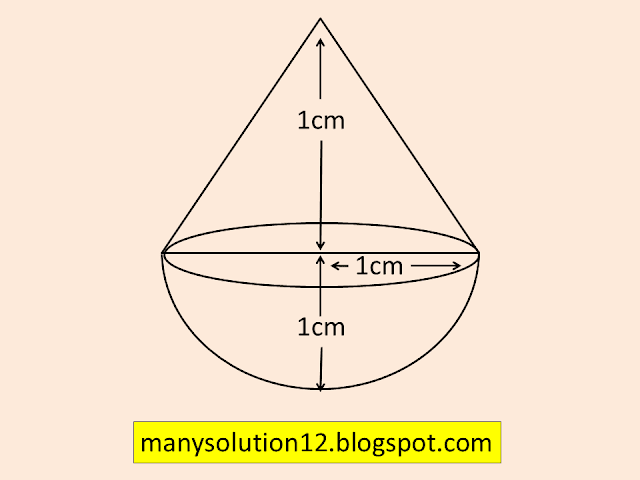
10th Maths 13.3

NCERT Class 10th solution of Exercise 13.1 NCERT Class 10th solution of Exercise 13.2 NCERT Class 10th Maths Projects Exercise 13.3 Take `pi = 22/7` unless stated otherwise. Q1. A metallic sphere of radius `text{4.2 cm}` is melted and recast into the shape of a cylinder of radius `text{6 cm}`. Find the height of the cylinder. `text{Sol. :}` `text{Given :}` `text{Radius of Sphere }R = 4.2 text{ cm}` `text{Radius of Cylinder }r = 6 text{ cm}` `text{To find :}` `text{Height of the Cylinder}` `text{Solve :}` `text{According to question}` `text{Volume of the Cylinder = Volume of the Sphere}` `pir^2h = 4/3piR^3` `h = (4piR^3)/(3pir^2)` `h = (4R^3)/(3r^2)` `h = (4times(4.2)^3)/(3(6)^2)` `h = (4times4.2times4.2times4.2)/(3times6times6)` `h = (4times4.2times0.7times0.7)/3` `h = (8.232)/3` `h = 2.744text{ cm}` `text{Answer :}` `text{The height of the cylinder 2.744 cm.` ☝ Like, Share, and Subscribe. Q2. Metallic spheres of radii `text{6 cm, 8 cm}` and `text{10 cm,}` ...