9th Maths 6.1

NCERT Class 9th solution of Exercise 6.2

NCERT Class 9th solution of Exercise 6.3

Exercise 6.1

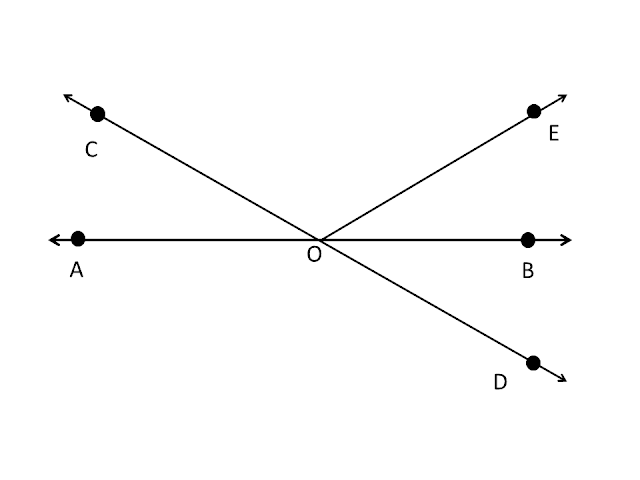
Q1. In the given figure lines AB and CD intersect at O, if ∠AOC+∠BOE=70° and ∠BOD = 40° then find the ∠BOE and reflex ∠COE.
Sol.
∠AOC=∠BOD_______(1) [Vertically opp. angles]
∠AOC=40°    ________(2) [ Given ∠BOD=40°]
∠AOC+∠BOE=70°____(3) [Given]
40°+∠BOE=70°                    [ from eq. (2) ]
∠BOE=70°-40°
∠BOE=30°__________(4)
Now
∠AOC+∠COE+∠BOE=180°   [ By Linear pair]
40°+∠COE+30°=180°           [ from eq. (2) & (4) ]         
∠COE=180°-70°
∠COE=110°
Reflex∠COE=360°-∠COE
Reflex∠COE=360°-110°
Reflex∠COE=250°
Answer :
The required ∠BOE=30° and reflex∠COE=250°.
Q2. In the figure lines, XY and MN intersect at O. If ∠POY=90° and a:b=2:3, find c.
Sol.
∠XOP+∠POY=180°    [ By linear pair ]
(∠XOM+∠MOP)+90°=180° [ Given ∠POY=90°]
(a+b)=180°-90°
a+b=90°
Sum of the ratio 
a+b=2+3
a+b=5
a=frac(2)(5)times90°
a=36°
b=frac(3)(5)times90°
b=54°_____________(1)
c+b=180°                     [ by linear pair ]
c+54=180°                   [ from eq. (1) ]
c=180°-54°
c=126°
Answer :
The required value of c=126°.
Q3. In the figure,∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.
Sol.
∠PQS+∠PQR=180°                    [ By linear pair ]
∠PQR=180°-∠PQS________(1) 
∠PRQ+∠PRT=180°                    [ By linear pair ]
∠PRQ=180°-∠PRT________(2) 
`∠PQR=∠PRQ                              [ Given ]
180°-∠PQS=∠PRT-180°            [ From eq. (1) & (2) ]
∠PQS=∠PRT
Proved.
Q4. In the figure, if x+y=w+z, then prove that: AOB is a line.
Sol.
x+y+w+z=360°____(1)  [By angle sum property of a point]
x+y=w+z         ____(2)  [ Given ]
x+y+x+y=360°
2x+2y=360°
2(x+y)=360°
x+y=frac(360°)(2)
x+y=180°
∠AOB=180°
AOB is a line.
Proved.
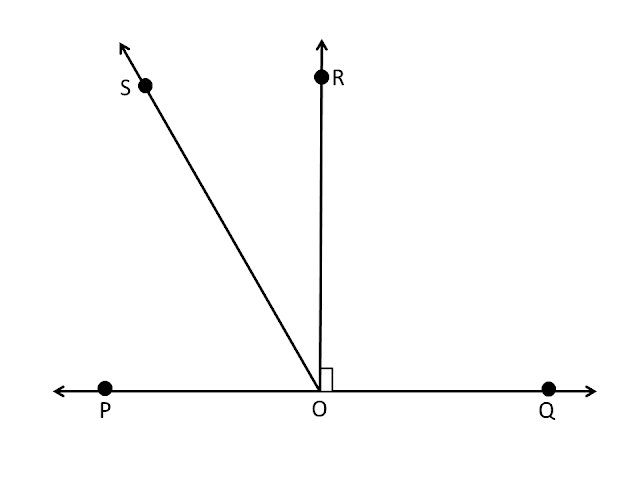
Q5. In the figure, POQ is a straight line. Ray OR is perpendicular to line PQ. OS is another ray lying between ray OP. Prove that:
∠ROS=frac(1)(2)(∠QOS-∠POS).
Sol.
∠POR+∠ROQ=180° [ By linear pair ]
∠POR+90°=180°     [ Given OR⊥PQ ]
∠POR=90°
So 
∠POR=∠ROQ_________(1)
∠POR=∠POS+∠ROS___(2)
∠ROQ=∠QOS-∠ROS___(3)
∠POS+∠ROS=∠QOS-∠ROS[ From eq. (1),(2) & (3) ]
∠ROS+∠ROS=∠QOS-∠POS
2∠RPS=∠QOS-∠POS
∠ROS=frac(1)(2)(∠QOS-∠POS)
Proved.
Q6. It is given that ∠XYZ=64° and XY is produced to point P. Draw a figure from the given information. If ray ∠YO bisects ∠ZYP, find ∠XYQ and reflex ∠QYP.

Sol.
∠ZYP+∠XYZ=180°  [ By linear pair ]
∠ZYP+64°=180°      [ Given ∠XYZ=64°]
∠ZYP=180°-64°
∠ZYP=116°
∠ZYQ+∠QYP=116°
∠ZYQ+∠ZYQ=116°  [Given Ray YQ bisect ∠ZYP ]
2∠ZYQ=116°
∠ZYQ=frac(116°)(2)
∠ZYQ=58°=∠QYP
∠XYQ=∠XYZ+∠ZYQ
∠XYQ=64°+58°    [ ∠XYZ=64°]
∠XYQ=122°
Reflex∠QYP=360°-∠QYP
Reflex∠QYP=360°-58°
Reflex∠QYP=302°
Answer :
The required ∠XYQ=122° and Reflex ∠QYP=302°.

Comments

Post a Comment

Popular posts from this blog

10th Maths Chapter 1

Chapter 1 Real Numbers Q1. Choose the correct option: 1. HCF of (96, 404) is : a)  4     b) 120     c) 11     d) 5 2. HCF of (6, 20) is : a) 20     b) 6     c) 120     d) 2 3. HCF of  (91, 21)  is : a) 91     b) 21     c) 7      d) 12 4. If the product of two numbers is 32 and LCM is 8 then its HCF is : a) 4     b) 2     c) 1     d) 00 5. If two positive integers p and q are expressed as p = ab² and q = a³b; a, b being prime numbers, then LCM. (p,q) is : a) ab     b) a²b²     c) a³b²     d) a³b³ Answer: 1. b, 2. c, 3. c, 4. a, 5. c Q2. Fill in the blanks: 1. HCF. (a, b)×LCM. (a, b) = ..................  . 2. If a = x^3y^2 and y = xy^3, where x, y are prime numbers, then HCF. (a, b) will be ............  . 3. sqrt3 is a ............. number. 4. Rational and irrational numbers both are .......... numbers...
Read more

CBSE 10th and 12th Result

Image
CBSE 10th & 12th Result 10वीं और 12वीं का रिजल्ट प्राप्त करने के लिए आवश्यक दस्तावेज  कक्षा 10वीं और 12वीं का रिजल्ट प्राप्त करने के लिए आवश्यक दस्तावेज Roll Number, Admit card ID  और अन्य सबमिट कर । 10वीं और 12वीं का रिजल्ट कहाँ से प्राप्त करें कक्षा  10वीं और  12वीं का रिजल्ट उम्मीदवार वेबसाइट को टच करके  CBSE 10th result  👈👈 या CBSE 10th result 👈👈 या CBSE 10th result  👈👈 या CBSE 12th result 👈👈 या CBSE 12th result 👈👈 या CBSE 12th result 👈👈 CBSE 10th result  👈👈 या CBSE 10th result 👈👈 या CBSE 10th result  👈👈 या CBSE 12th result 👈👈 या CBSE 12th result 👈👈 या CBSE 12th result 👈👈 पर नतीजे देख सकते है । 10वीं और 12वीं के उम्मीदवारों को सलाह  यह परीक्षा जीवन का एक हिस्सा है, सारा जीवन नहीं । इस परीक्षा के परिणाम की कमियों से परेशान न होकर संयम और धैर्यपूर्वक स्वीकार करें । आपको आने वाले समय में इन कमियों को दूर करने का प्रयास करना होगा । जीवन में करने के लिए बहुत कुछ है ।  10वीं और 12वीं के बाद आगे क्या करें? -...
Read more

RSKMP 5th & 8th Result

Image
RSKMP 5th & 8th Result राज्य शिक्षा केंद्र  [RSKMP ] भोपाल म.प्र. 5वीं और 8वीं का रिजल्ट प्राप्त करने के लिए आवश्यक दस्तावेज  कक्षा 5वीं और 8वीं का रिजल्ट प्राप्त करने के लिए आवश्यक दस्तावेज रोल नंबर, आवेदन क्रमांक, समग्र आईडी और अन्य सबमिट कर । Like, Share, and Subscribe. 5वीं और 8वीं का रिजल्ट कहाँ से प्राप्त करें कक्षा  5वीं और  8वीं का रिजल्ट उम्मीदवार नीचे दी वेबसाइट को टच करके 5th और 8th का रिजल्ट  🫲 5th और 8th का रिजल्ट  🫲 5th और 8th का रिजल्ट  🫲 5th और 8th का रिजल्ट  🫲 पर नतीजे देख सकते है । 5वीं और 8वीं के उम्मीदवारों को सलाह  यह परीक्षा जीवन का एक हिस्सा है, सारा जीवन नहीं । इस परीक्षा के परिणाम की कमियों से परेशान न होकर संयम और धैर्यपूर्वक स्वीकार करें । आपको आने वाले समय में इन कमियों को दूर करने का प्रयास करना होगा । जीवन में करने के लिए बहुत कुछ है ।  ------x---- राज्य शिक्षा केंद्र  [RSKMP ] भोपाल म.प्र. 5वीं और 8वीं का रिजल्ट प्राप्त करने के लिए आवश्यक दस्तावेज  कक्षा 5वीं और 8वीं का रिजल्ट प्राप्त करने...
Read more