9th Mahts 6.3
NCERT Class 9th solution of Exercise 6.1
NCERT Class 9th solution of Exercise 6.2
Exercise 6.3
Q1. In the given figure, sides `QP` and `RQ` of `△PQR` are produced to points `S` and `T` respectively. If `∠SPR=135°` and `∠PQT=110°`, find `∠PRQ`.
Sol.
`∠PQT+∠PQR=180°` [ By linear pair. ]
`110°+∠PQR=180°` [ Given `∠PQT=110°` ]
`∠PQR=180°-110°`
`∠PQR=70°`
`∠PRQ+∠PQR=∠SPR`
[ By exterior angle property ]
`∠PRQ+70°=135°` [ Given `∠SPR=135°` ]
`∠PRQ=135°-70°`
`∠PRQ=65°`
Answer :
The required value of `∠PRQ=65°`.
Q2. In the given figure, `∠X=62°, ∠XYZ=54°`. If `YO` and `ZO` are the bisectors of `∠XYZ` and `∠XZY` respectively of `△XYZ`, find `∠OZY` and `∠YOZ`.
Sol. :
In `△XYZ`,
`∠YXZ+∠XYZ+∠XZY=180°`
[ By Angle sum property of `△`]
`62°+54°+∠XZY=180°`
`∠XZY=180°-62°-54°`
`∠XZY=180°-116°`
`∠XZY=64°`
`∠XZO=∠OZY=frac(1)(2)times∠XZY`
[ `ZO` is bisect `∠XZY`]
`∠XZO=∠OZY=frac(1)(2)times64°`
[ Given `∠XZY=64°`]
`∠XZO=∠OZY=32°`
`∠XYO=∠OYZ=frac(1)(2)times∠XYZ`
[ `YO` is bisect `∠XYZ` ]
`∠XYO=∠OYZ=frac(1)(2)times54°`
[ Given `∠XYZ=54°` ]
`∠XYO=∠OYZ=27°`
In `△YOZ`
`∠OYZ+∠OYZ+∠YOZ=180°`
[ By angle sum property of `△`]
`27°+32°+∠YOZ=180°`
`∠YOZ=180°-27°-32°`
`∠YOZ=180°-59°`
`∠YOZ=121°`
Answer :
The required `∠OZY=32°` and `∠YOZ=121°`.
Q3. In the given figure, if `AB∥DE, ∠BAC=35°` and `∠CDE=53°`, find `∠DCE`
Sol. :
`AB∥DE` and `AE` is transversal. [ Given ]
`∠CED=∠BAC` [ Alternate angles ]
`∠CED=35°`
In `△CDE`
`∠DCE+∠CDE+∠CED=180°`
[ By angle sum property of `△` ]
`∠DCE+53°+35°=180°`
[Given `∠CDE=53°`]
`∠DCE=180°-88°`
`∠DCE=92°`
Answer :
The required value `∠DCE=92°`.
Sol. :
In `△PRT`
`∠PTR+∠RPT+∠PRT=180°`
[ By angle sum property of `△` ]
`∠PRT+95°+40°=180°`
[ Given `∠RPT=95°` & `∠PRT=40°`]
`∠PRT=180°-95°-40°`
`∠PRT=180°-135°`
`∠PRT=45°`
`PQ` intersect `RS` at point `T`
`∠QTS=∠PRT` [ Vertically opp. angles]
`∠QTS=45°`
In `△SQT`
`∠SQT+∠TSQ+∠QTS=180°`
[ By angle sum property of `△`]
`∠SQT+75°+45°=180°`
[ Given `∠TSQ=75°`]
`∠SQT=180°-75°-45°`
`∠SQT=180°-120°`
`∠SQT=60°`
Answer :
The required value of `∠SQT=60°`.
Sol. :
`PQ∥SR` and `QR` is transversal
`∠PQR=∠QRT` [Alternat angles ]
According to figure
`∠PQS+∠SQR=∠QRT`
`x+28°=65°`
[Given `∠SQR=28°` & `∠QRT=65°`]
`x=65°-28°`
`x=37°`
In `△PQS`
`∠QPS+∠PQS+∠PSQ=180`
[ By angle sum property of `△`]
`90°+37°+y=180°` [ Given `∠QPS=90°`]
`y=180°-90°-37°`
`y=180°-127°`
`y=53°`
Answer :
The required value of `x=37°` & `y=53°`.
According to figure
`∠PRS=∠QPS+∠PQR`______(1)
[ By exterior angle property ]
`∠TRS=∠QTR+∠TQR`_____(2)
[ By exterior angle property ]
Since `QT` & `RT` are bisectors of `∠PQR`
& `∠PRS` [Given]
`∠TQR=frac(1)(2)∠PQR`___(3)
`∠TRS=frac(1)(2)∠PRS`____(4)
`∠TRS=frac(1)(2)∠QPR+frac(1)(2)∠PQR`___(5)
[ by eq.(1) &(4)]
`∠QTR+∠TQR=frac(1)(2)∠QPR+frac(1)(2)∠PQR`
[ by eq.(2) & (5) ]
`∠QTR+frac(1)(2)∠PQR=frac(1)(2)∠QPR+frac(1)(2)∠PQR`
`∠QTR=frac(1)(2)∠QPR`
Proved.

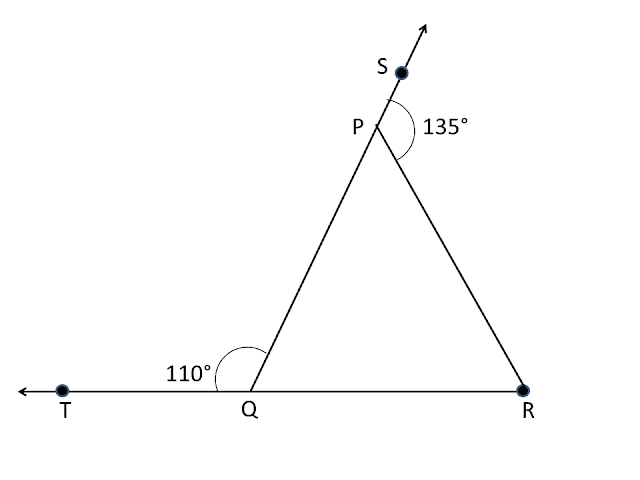







Comments