9th Maths Projects
9th Maths Project
Like, Share, and Subscribe.
9th Project Topics
1. Establish Heron's formula to find the area of a triangle.
2. Find the total surface area and volume of a class 9th math book by measuring its length, breadth, and height.
3. Briefly describe the biography and achievements of any three mathematicians.
4. By making a polygon, measure all its exterior angles and find their sum.
5. Explain geometric applications in daily life.
6. Explain the surface area of a sphere with the help of two examples.
7. Explain the volume of a sphere with the help of two examples.
8. Explain the presentation of data with the help of two examples.
9. Explain the probability with the help of three examples.
10. Explain the law of exponents for real numbers with the help of two examples.
11. Explain the solution of a linear equation with the help of two examples.
12. Explain the polynomials with the help of two examples.
13. Explain the circles and their related terms with the help of two examples.
14. Explain the congruence of triangles with the help of three examples.
15. Explain the basic terms and definitions of lines and angles with the help of two examples.
Project No. 1
Objective: Establish Heron's formula to find the area of a triangle.
Life Introduction:
Heron was born in about 10 AD possibly in Alexandria in Egypt. He was a Greek Engineer and Mathematician who was active in his native city Alexandria, Roman Egypt. Heron was determine the area of the triangle using only the length of its sides.
Works and Contribution:
He worked in applied mathematics. His works on mathematical and physical subjects are so numerous and varied that he is considered to be an encyclopedic writer in these fields. His geometrical works deal largely with problems on mensuration written in three books. Book I deals with the area of squares, rectangles, triangles, trapezoids (trapezia), various other specialised quadrilaterals, regular polygons, circles, surfaces of cylinders, cones spheres, etc. In this book, Heron has derived the famous formula for the area of a triangle in terms of its three sides.
Heron's Formula:
The formula given by Heron about the area of a triangle is also known as Heron's formula. It is stated as:
Area of triangle `= sqrt(s(s-a)(s-b)(s-c))`
where
a, b and c are the lengths of sides of the triangle,
s = semi-perimeter,
half the perimeter of the triangle `s = (a + b + c)/2`
Need of formula:
This formula is helpful when the sides of the triangle are given and where it is not possible to find the height of the triangle easily. Let us apply it to calculate the area of the triangle.
Example 1. A traffic signal board, indicating 'SCHOOL AHEAD', is an equilateral triangle with a side 'a'. Find the area of the signal board, using Heron's formula. If its perimeter is `180cm`, what will be the area of the signal board?
Sol. :
Semi perimeter `S=(a+a+a)/2=(3a)/2`
By Heron's formula:
Ar. of `triangle=sqrt(S(S-a)(S-b)(S-c))`
Ar. of `triangle=sqrt((3a)/2((3a)/2-a)((3a)/2-a)((3a)/2-a))`
Ar. of `triangle=sqrt((3a)/2(a/2)(a/2)(a/2))`
Ar. of `triangle=sqrt(3)/4a^2` square unit.
The Perimeter of the equilateral `triangle=3a`
`180=3a`
`a=180/3`
`a=60`
Area of `triangle=sqrt3/4a^2`
Area of `triangle=(60)^2/4sqrt3cm^2`
Area of `triangle=(60times60)/4sqrt3cm^2`
Area of `triangle=900sqrt3cm^2`
Answer :
Area of the signal board `triangle=900sqrt3cm^2.`
========X=======
Project No. 2
Objective: Find the total surface area and volume of a class 9th math book by measuring its length, breadth, and height.
Material Required :
9th math book, Pen, Scale.
i)
Total Surface Area of math book = Surface Area of Cuboid
Total Surface Area of math book = `2(lb + bh + hl) cm^2`
ii)
The volume of math book = Volume of Cuboid
The volume of math book`= l times b times h cm^3`
Where
`l = `length of a math book,
`b = `breadth of a math book,
`h = `height of math book,
Solution:
Length of math book `l= 27 cm`
Breadth of math book `b= 20 cm`
Height of math book `h= 2 cm`
Surface Area of math book `= 2( lb + bh + hl)`
`= 2( 27times20 + 20times2 + 2times 27)`
`= 2( 540 + 40 + 54 )`
`= 2times634`
`= 1268 cm^2`
Volume of math book `= l times b times h`
`= 27 times 20 times 2`
`= 1080 cm^3`
Result:
The total surface area of the math book is `1268 cm^2` and the Volume of the math book is `1080cm^3.`
========X=======
Project No. 3
Objective: Briefly describe the biography and achievements of any three mathematicians.
Varahmihir:
Biography
Varahmihir's father's name was Adityadas and his mother's name was Satyavati. Adityadas was a scholar of mathematics and astrology. He lived in Kapithika ( Kaytha) village 20 km. from Ujjain. It is a matter of honour that this great scholar of mathematics belonged to M.P.
Acharya Varahmihir was born in Kapithika (Ujjain) presently known as village Kaytha.
Achievements
Kapithya Gurukul established by him in the memory of his father remained a famous centre of learning for 700 years. This Gurukul is known as the Ujjain School in the history of mathematics. Kapithika Gurukul has an important contribution to the development of Mathematics. Brahmgupt, Mahaviracharya, and Bhaskaracharya were the mathematicians of this Gurukul.
Kank a scholar of Ujjain went to the court of Abba Sayeed Khalifa Almansoor of Baghdad in 770 A.D. This way the Hindu number system reached Arabs. Kank taught mathematics and astrology to Arabin scholars. They translated 'Brahmsphut Sidhant' of Brahmgupt with the help of Kank in Arbi.
With this extraordinary contribution of India to the rest of the world. French scholar M.F. Naad discovered that in Syria during the mid-seventh century these Hindu numerals were well known and appreciated.
Bhaskaracharya:
Biography & Achievements:
World-renowned Bhaskaracharya the author of Sidhant Shiromani was born in Maharashtra. His birth time is known as 1114 A.D. He wrote 'Sidhant Shiromany' at the age of 36 years. It contains two parts. Ganitadhyay and Goladhyay. His second important work is 'Leelavati', which contains descriptions of arithmetic, area, cube root, interest etc. During that period teaching was done through writing on board(pati) or on earth by figures Leelavati is Patiganit.
Leelavati contains questions and answers on the value of π, areas of triangles and quadrilaterals, the volume of spheres etc.
Akbar got Bhaskarachary's works translated, and Kolbruck Taylor translated these in English Aryabhatta popularised Indian astrology and mathematics. Bhaskara's creation spread these in Europe and Western countries with more strength.
Bodhayan:
Biography & Achievements:
In India geometry evolved in the Vedic period to worship through the use of the construction of different altars and fire pits. A special roap called 'Sulv' was used for measurement during the construction of altars. Much information has been given in the Sulva-Sutra written by Vedic sages during 800 B.C. The so-called Pythagoras theorems statement is found in the oldest Sulva-Sutra is known as Bodhayan Sulva-Sutra (about 800 B.C.), the statement is the diagonal of a rectangle produces the two areas which are produced by both sides. The proof of the Pythagoras theorem is found in the construction methods described in Sulva-Sutras. Sulva-Sutras contain the formulas for finding areas of various geometrical figures.
========X=======
Project No. 4
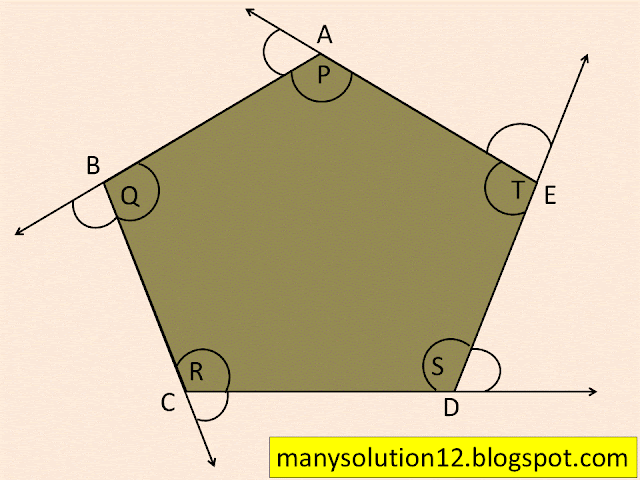
Objective: By making a polygon, measure all its exterior angles and find their sum.
Polygon:
'Poly' means many and 'gon' means sides. So, a polygon is a closed figure having many sides. A polygon of n sides of n sides is also called n-gon.
Types of Polygon
There are two types of polygons:
i) Convex Polygon
ii) Concave Polygon.
Sum of the Interior angle of a regular pentagon
`=(n-2)180^circ`
`=(5-2)180^circ`
`=3times180^circ`
`=540^circ`
By making a polygon,
The sum of the measures of the exterior angles of any polygon is `360^circ`.
Let us prove it by taking an example.
Example.
`ABCDE` is a pentagon.
To Prove:
The sum of exterior angles of the pentagon is `360^circ`
`angle A + angle B + angle C + angle D + angle E = 360^circ`
Proof:
`angle A + angle P = 180^circ`__(1)[by linear pair]
`angle B + angle Q = 180^circ`__(2)[by linear pair]
`angle C + angle R = 180^circ`__(3)[by linear pair]
`angle D + angle S = 180^circ`__(4)[by linear pair]
`angle E + angle T = 180^circ`__(5)[by linear pair]
We Add equations (1), (2), (3), (4), and (5)
`(angle A+angleP)+(angleB+angleQ)+(angleC+angle R)``+(angle D+angle S)+(angle E+angle T)`
`=180^circ+180^circ+180^circ+180^circ+180^circ`
`angle A+angle B+angleC+angle D+angle E+angleP+angleQ``+angle R+angleS+angleT`
`=900^circ`
`angleA+angleB+angleC+angleD+angleE+540^circ``=900^circ`
`angleA+angleB+angleC+angleD+angleE =900^circ`` - 540^circ`[ Sum of all interior angles of pentagon is `540^circ`]
`angleA+angleB+angleC+angleD+angleE = 360^circ`
Each exterior angle of a regular polygon of `n` sides is equal to `((360^circ)/n)`
Each exterior angle of a regular pentagon of `5` sides is equal to `((360^circ)/5)=72^circ`
========X=======
Project No. 5
Objective: Explain geometric applications in daily life.
Geometry
A glance at the History of mathematics shows that geometry was studied in the early Vedic period also. The information about mathematics of that period is available in the form of the Shulv-Sutra (3000 B.C.) from Kalap named Vedang. The roap used in the measurement of altars is called Shulva. Shulva means 'presentation of information in the short form. The theorem commonly named as 'Pythagoras theorem', construction was explained in Shulva Sutras (Bodhayan Shulva Sutra) Shulva Sutra is known by the name of their creators like Bodhayan, Aapstambh, Katyayan, Manav, Maitrayan, etc. Some of these are (1) Garuvedi (2) Kurmvedi.
Some examples of Shulve Sutra Geometry are given below:
i) Construction of triangles, squares, rectangles, and other typical geometrical figures.
ii) Construction of geometrical figures whose area is the sum or difference of the area of some given figures.
iii) To construct a square from a circle and vice-versa.
Aryabhatt, Bhaskara first, Brahmgupt, and Mahavira have remarkable contributions to the field of geometry.
Aryabhata described geometry in various sections of his books. He mainly wrote the formulas for the area of triangles, quadrilaterals, circles, and volumes of solids.
In the 'Kshetra vyavhar' chapter of Bhaskaracharya's Leelawati, he described the areas of right triangles and quadrilaterals circles, and the surface area and volume of spheres.
The modern study of algebra started with definitions, axioms, propositions, and theorems described in the book 'Elements' by Greek mathematician Euclid. In the work of 13 volumes, number principles and elementary algebra are also discussed with geometry. It is understood that Euclid developed this work in 323 B.C.
The word geometry is made up of two Greek words 'geo and metro'. Geo means 'the earth' and metron means 'to measure. Thus, the origin of geometry is as old as the development of human civilization, when human beings required the measurement of the land. Probably, Egyptians were the first to study geometry. Their main interest was in the problem of mensuration, as the area to find rectilinear figures like triangles and rectangles. After this Babylonian, evolved formulas for finding areas of different rectilinear figures. These formulas are found in the Babylonian book Rhind Papyrus (1650 B.C.). Egyptians and Babylonians both mostly used geometry for practical works and could not work for the development of geometry, But the presentation of geometry as systematic science is credited to Greeks.
========X=======
Project No. 6
Explain the surface area of a sphere with the help of two examples.
A sphere is a three-dimensional figure (solid figure), which is made up of all points in the space, which lie at a constant distance called the radius, from a fixed point called the centre of the sphere.
Note: A sphere is like the surface of a ball. The word solid sphere is used for the solid whose surface is a sphere.
The surface area of a sphere of radius r = 4 times the area of a circle of radius `r = 4 times(pir^2)`
Surface Area of a Sphere `= 4pi r^2`
The sphere has only one surface, which is curved.
Hemisphere is a half part of a sphere.
Curved Surface Area of a Hemisphere `=2pir^2`
Now take the two faces of a hemisphere, its surface area `2pir^2 + pir^2`
Total Surface Area of a Hemisphere `=3pir^2`
See more examples click (Ex13.4)
========X=======
Project No. 7
Explain the volume of a sphere with the help of two examples.
The measure of occupied space is called the Volume of the object.
Let us see how to go about measuring the volume of a sphere. First, take two or three spheres of different radii, and a container big enough to be able to put each of the spheres into it, one at a time. Also, take a large trough in which you can place the container. Then, fill the container up to the brim with water.
So, Carefully place one of the spheres in the container. Some of the water from the container will overflow into the trough in which it is kept. Carefully pour out the water from the trough into a measuring jar and measure the water flowing.
The volume of a Sphere `= 4/3pir^3`
The volume of a Hemisphere `=2/3pir^3`
Let's take examples to illustrate the use of these formulae.
See more examples click (Ex 13.8)
========X=======
Project No. 8
Explain the presentation of data with the help of two examples.
The collection of data is over, the investigator has to find out ways to present them in a form that is meaningful, easily understood, and gives its main features at a glance. Let us now recall the various ways of presenting the data through some examples
See more examples click (Ex 14.2)
========X=======
Project No. 9
Explain the probability with the help of three examples.
The uncertainty of 'probably' etc can be measured numerically by means of 'probability' in many cases.
Though probability started with gambling, it has been extended to the fields of Commerce, Biological Sciences. Medical Sciences, Physical Sciences, Weather forecasting, etc.
Probability measure the chance of occurrence of a particular outcome in an experiment.
Experimental or empirical probability is P(E).
P(E) `= text{No. of trials in which the event happened}/text{The total number of trials}`
P(E) `= text{n(E)}/text{n(S)}`
Let us consider some examples.
See more examples click (Ex 15.1)
========X=======
Project No. 10
Explain the law of exponents for real numbers with the help of two examples.
i) `a^m.a^n = a^(m+n)`
ii) `a^m/a^n = a^(m-n), m gt n`
iii) `(a^m)^n = a^(mn)`
iv) `a^mb^m = (ab)^m`
v) `a^0 = 1`
vi) `a^(-1) = 1/a`
where `a` is the base and `m` and `n` are the exponents.
Let us consider some examples
See more examples click (Ex 1.6)
========X=======
Project No. 11
Explain the solution of a linear equation with the help of two examples.
Linear equation in one variable is ax + c = 0.
where x is variable.
Every linear equation in one variable has a unique solution.
Linear equation in two variables is ax + by + c = 0
where x and y are variables.
A linear equation in two variables has infinitely many solutions.
Note that an easy way of getting a solution is to take x = 0 and get the corresponding value of y. Similarly, we can put y = 0 as the corresponding value of x.
See more examples click (Ex 4.2)
========X=======
Project No. 12
Explain the polynomials with the help of two examples.
A polynomial p(x) in one variable x is an algebraic expression in x of the form
`p(x) = a_nx^n + a_(n-1)x^(n-1) + ....... + a_2x^2`
`text{ }+ a_1x + a_0,`
where `a_0, a_1, a_2, ....., a_n` are constants and `a_n ne 0`.
`a_0, a_1, a_2,....a_n` are respectively the coefficients of `x^0, x^1, x^2, .....,x_n,` and `n` is called the degree of the polynomial. Each of `a_nx^n, a_(n-1)x^(n-1), ...., a_0,` with `a_n ne 0`, is called a term of the polynomial `p(x).`
1. Polynomials having only one term are called monomials ('momo' means 'one').
`p(x) = x`
2. Polynomials having only two terms are called binomials ('bi' means 'two').
`p(x) = x + x^2`
3. Polynomials having only three terms are called trinomials ('tri' means 'three').
`p(x) = u + u^2 -2`
4. The highest power of the variable in a polynomial is the degree of the polynomial.
5. A polynomial of degree one is called a linear polynomial.
`p(x) = ax + bx + c`
6. A polynomial of degree two is called a quadratic polynomial.
`p(x) = ax^2 + bx + c`
7. A polynomial of degree three is called a cubic polynomial.
`p(x) = ax3 + bx^2 + c`
See more examples click (Ex 2.1)
========X=======
Project No. 13
Explain the circles and their related terms with the help of two examples.
The collection of all the points in a plane, which are at a fixed distance from a fixed point in the plane, is called a circle.
Note that the line segment joining the centre and any point on the circle is also called a radius of the circle. That is, 'radius' is used in two senses in the sense of a line segment and its length.
A circle divides the plane on which it lies into three parts. They are:
i) inside the circle. which is also called the interior of the circle,
ii) the circle,
iii) outside the circle, which is also called the exterior of the circle.
The chord that passes through the centre of the circle, is called the diameter of the circle. The diameter is the most extended chord and all diameters have the same length, which is equal to two times the radius.
See more examples click (Ex 10.2)
========X=======
Project No. 14
Explain the congruence of triangles with the help of three examples.
'Congruent' means equal in all respects or figures whose shapes and sizes are both the same.
The congruent symbol is `cong`.
Now, draw two circles of the same radius and place one on the other. They cover each other completely and we can call them congruent circles.
Repeat this activity by placing one square on the other with sides of the same measure or by placing two equilateral triangles of equal sides on each other. You will observe that the squares are congruent with each other and so are the equilateral triangles.
Note that in congruent triangles corresponding parts are equal and we write in short 'CPCT' for corresponding parts of congruent triangles.
See more examples click (Ex 7.1)
========X=======
Project No. 15
Explain the basic terms and definitions of lines and angles with the help of two examples.
A part of (or portion) of a line with two endpoints is called a line segment and a part of a line with one endpoint is called a ray.
The line segment `AB` is denoted by `overline(AB)`.
The ray `AB` is denoted by `vec(AB)`.
If three or more points lie on the same line, they are called collinear points otherwise they are called non-colinear points.
An angle is formed when two rays originate from the same endpoint. The rays making an angle are called the arms of the angle and the endpoint is called the vertex of the angle.
An acute angle measures between `0^circ` and `90^circ`, whereas a right angle is exactly equal to `90^circ`. An angle greater than `90^circ` but less than `180^circ`is called an obtuse angle. A straight angle is equal to `180^circ`. An angle that is greater than `180^circ` but less than `360^circ` is called a reflex angle. Further, two angles whose sum is `90^circ` are called complementary angles, and two angles whose sum is `180^circ` are called supplementary angles.
See more examples click (Ex 6.1)
========X=======






Comments