9th Maths 6.2
NCERT Class 9th solution of Exercise 6.1
NCERT Class 9th solution of Exercise 6.3
Exercise 6.2
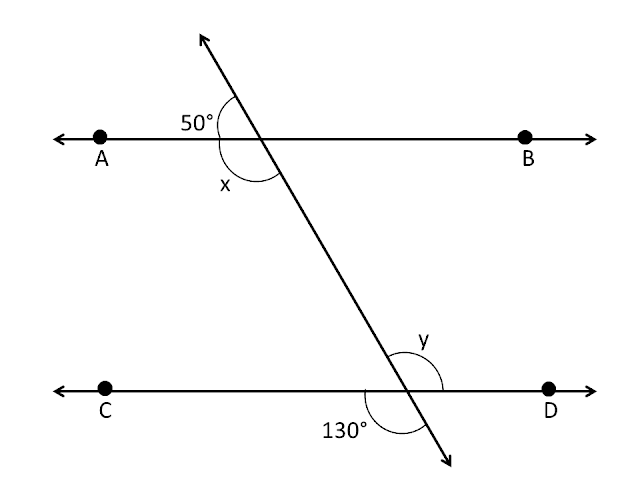
Q1. In the given figure, find the values of x and y and then show that AB∥CD.
According to the given figure
x+50=180° [ By linear pair ]
x=180-50°
x=130°____(1)
y=130°____(2) [ Vertically opp. angles ]
x=y=130° [ By eq. (1) & (2) ]
AB∥CD. [ Alternate angles are equal ]
Proved.
Sol. :
Q2. In the given figure, if AB∥CD, CD∥EF and y:z=3:7,find x.
Let ST is transversal line intersects AB, CD, & EF at P, Q, & R respectively,
According to the given figure
∠DQR=∠PQC=y [ Vertically opp. angles and given ∠PQC=y]
∠DQR=y
∠DQR+∠QRF=180° [ linear pair and given ∠QRF=z ]
y+z=180° [ Sum of interior angles on the same side ]
The Sum of the ratio of y & z is 3+7=10
y=frac(3)(10)times180°
y=54°
z=frac(7)(10)times180°
x=z=126° [Alternate angles are equal]
Answer :
The required value of y=54° & z=x=126°.
Q3. In the given figure, if AB∥CD, EF⊥CD and ∠GED=126° find ∠AGE, ∠GEF and ∠FGE.
Sol. :
According to the given figure
GE is transversal of AB∥CD
∠AGE=∠GED [ Alternate angle ]
∠AGE=126° [ Given ∠GED=126° ]
∠GEF+∠FED=∠GED
∠GEF+90°=126° [ Given EF⊥CD ]
∠GEF=126°-90°
∠GEF=36°
∠FGE+∠GED=180°
∠FGE+126°=180°
∠FGE=180°-126°
∠FGE=54°
Answer :
The required values of ∠AGE=126°, ∠GEF=36°, and ∠FGE=54°
Q4. In the given figure, if PQ∥ST, ∠PQR=110° and ∠RST=130°, find ∠QRS.
Sol. :
According to the given figure PQ∥ST
Construction :
Draw RD∥ST through R.
Proof :
ST∥RDand SR is transversal.
∠SRX+∠RST=180° [ Sum of interior angles of the same side.]
∠SRX+130°=180° [ Given RST=130° ]
∠SRX=180°-130°
∠SRX=50°_________(1)
PQ∥RX and QR is transvesal.
∠QRX=∠PQR [ Alternate angles and given ∠PQR=110° ]
∠QRX=110°
∠QRS+SRX=110°
∠QRS+50°=110° [ from eq. (1) ]
∠QRS=110°-50°
∠QRS=60°
Answer :
The required ∠QRS=60°.
Q5. In the given figure, if AB∥CD, ∠APQ=50° and ∠PRD=127°, find x and y.
Sol. :
According to the given figure
AB∥CD and PQ is transversal
∠PQR=∠APQ [ Alternate angles ]
x=50° [Given PQR=x and APQ=50°]
∠PQR+∠QPR=∠PRD [Exterior angle property ]
50°+y=127° [Given ∠PRD=127° ]
y=127°-50°
y=77°
Answer :
The required values are x=50° & y=77°`.
Q6. In the given figure, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B. The reflected ray moves along the path BC and strikes the mirror RS at C and again reflected back along CD. Prove that AB∥CD.
Sol. :
AB is incident ray strikes at point B of mirror PQ and reflected along BC.
∠PBA=∠QBC_____(1) [ By the law of reflection ]
BC is incident ray strikes at point C of mirror RS and reflected along CD
∠BCR=∠DCS_____(2) [ By the law of reflection ]
PQ∥RS and transversal BC intersects, then at the point B and C
∠QBC=∠BCR_____(3) [ Alternate angles ]
∠PBA+∠ABC+∠QBC=∠BCR+∠BCD+∠DCS=180°___(4)
[Sum of the angles at a point of line ]
∠PBA=∠QBC=∠BCR=∠DCS [ from eq. (1), (2) & (3) ]
∠PBA+∠QBC=∠BCD+∠DCS_______(5)
∠ABC=∠BCD [ from eq. (4) - (5) ]
∠ABC and ∠BCD are alternate angles.
AB∥CD
Proved.
Comments