9th Maths 5.1
NCERT Class 9th solution of Exercise 5.2
Exercise 5.1
Q1. Which of the following statements are True and which are False? Give reason for your answers :
i) Only one line can pass through a single point.
ii) There are an infinite number of lines which pass through two different points.
iii) A terminated line can be produced infinitely on both the sides.
iv) If two circles are equal, then their radius are equal.
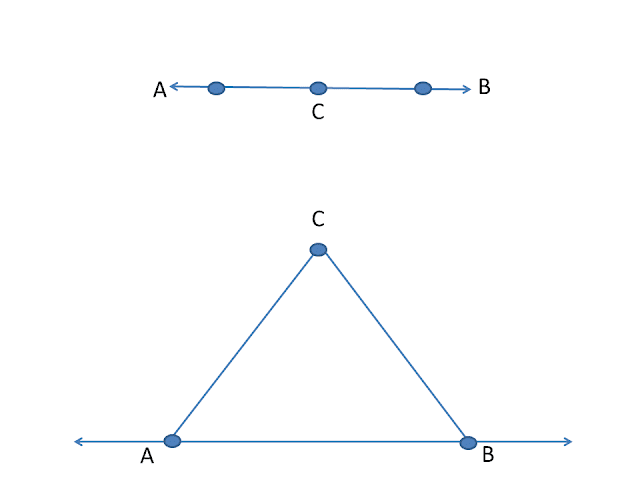
v) In the following figure if `AB=PQ` and `PQ=XY`, then `AB=XY`.
Answer :
i) False. Infinitely many lines can pass through a single.
ii) False. One and only one line can pass through two different points.
iii) True. A terminated line can be produced indefinitely.
iv) True. If you superimpose the bounded by one circle on the other, then they coincide. So, their certres and boundaries coincide. Therefore, their radii will coincide.
v) True. Things which are equal to the same things are equal to one another.
Q2. Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they and how might you define them?
i) Parallel lines, ii) Perpendicular lines, iii) Line segment, iv) Radius of a circle, v) Square.
Answer :
i) Parallel lines: Two lines that do not intersect each other if produced indefinitely in both sides, are called parallel lines.
Here `AB∥CD`.
ii) Perpendicular lines: The angle between two lines is 90°, which are called perpendicular lines.
Here `AB⊥CD` or `CD⊥AB`
iii) Line segment: The distance between any two points on a straight line is called the line segment.
Here lies segment `CD` of lie `AB`.
iv) Radius of a circle: The distance between the centre of the circle and any point of the circumference of the circle is called the radius of a circle.
It is denoted by `r`.
Here radius `r=OP`.
v) Square: A four-sided closed figure whose all sides are equal and each angle is 90° is called square.
Here Square `ABCD`.
Q3. Consider two postulates given below :
i) Given any two distinct points `A` and `B`, there exist a third point C which is in between `A` and `B`.
ii) There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid's postulates? Explain.
There are several undefined terms which the student should list. They are consistent because they deal with two different situations:
i) says that given two points `A` and `B`, there is a point `C` lying on the line in between them;
ii) says that given `A` and `B`, you can take `C` not lying on the line through `A` and `B`.
These 'postulates' do not follow from Euclid's postulates. However, they follow from Axiom5.1.
Q4. If a point C lies between two points. `A` and `B` such that `AC = BC`, then prove that `AC=frac(1)(2)AB`. Explain by drawing the figure.
Sol. :
To prove: `AC=frac(1)(2)AB`
Proof:
`AC=BC`
`AC+AC=BC+AC` [Add `AC` both side ]
`2AC=AB` [`BC+AC=AB`]
`AC=frac(1)(2)AB` [Euclid's axiom-7]
Proved.
Q5. In question 4 point `C` is called a mid-point of line segment `AB`. Prove that every line segment has one and only one mid-point.
Sol. :
`C` is the mid-point of the line segment `AB`.
`AC=CB=frac(1)(2)AB`____________(i)
`D` is the mid-point of line segment `AB`.
`AD=DB=frac(1)(2)AB`____________(ii)
`AC=AD` [from equation i) and ii) ]
Therefore line segment `AC` coincides the line segment `AD`.
Thus, every line segment has one and only one mid-point.
Q6. In the given figure if `AC=BD` then prove that `AB=CD`.
Given: `AC=BD`
To prove: `AC=CD`
Proof:
`AC=BD`
`AB+BC=BC+CD` [`AC=AB+BC` and `BD=BC+BD`]
`AB+BC-BC=BC+CD-BC`[Euclid's axiom-3]
`AB=CD`
Q7. Why is axiom-5, in the list of Euclid's axioms considered a 'Universal Truth'? (Note that the question is not about the fifth postulate.
Answer:
Since this is true for anything in any part of the world, this is a universal truth.











Comments