10th Maths 13.1

Exercise 13.1

Q1.

$2$ cubes each of volume

$text{64 cm}^3$ are joined end to end. Find the surface area of the resulting cuboid.

$text{Sol. :}$

$text{Given :}$

$text{Volume of cube 64 cm}^3$

$text{To find :}$

$text{The Surface area of the resulting cuboid.}$

$text{Solve :}$

$text{Volume of cube = (side)}^3$

$64 = text{(side)}^3$

$(4)^3 = text{(side)}^3$

$text{side = 4 cm}$

After join

$2$ cubes the resulting cuboid

$text{Height = 4cm, Length = 8 cm, Breadth = 4 cm}$

$text{Surface Area of Cuboid = 2(LB + BH + HL)}$

$text{S A of Cuboid = 2}(8 times 4 + 4 times 4 + 4 times 8)$

$text{S A of Cuboid = 2}(32 + 16 + 32)$

$text{S A of Cuboid = 2}(80)$

$text{S A of Cuboid = 160 cm}^2$

$text{Answer:}$

$text{The Surface Area of resulting Cuboid is 160 cm}^2.$

☝

Like, Share, and Subscribe.

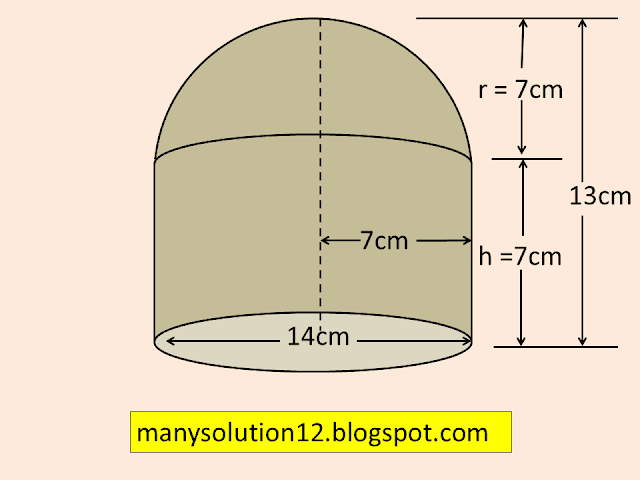
Q2. A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is

$text{14 cm}$ and the total height of the vessel is

$text{13 cm}$ . Find the inner surface area of the vessel.

$text{Sol. :}$

$text{Given :}$

$text{The radius of the vessel is }14/2 = 7 text{cm}$

$text{The height of the Cylinder is 6 cm}$

$text{To find :}$

$text{inner S A of the vessel}$

$text{Solve :}$

$text{inner S A of the vessel}$

$text{= SA of hemisphere + SA of Cylinder}$

$= 2pir^2 + 2pirh$

$= 2pir(r + h)$

$= 2 times 22/7 times 7(7 + 6)$

$= 44(13)$

$= 572 text{cm}^3$

$text{Answer :}$

$text{inner S A of the vessel 572 cm}^3$ .

Q3. A toy is in the form of a cone of radius

$text{3.5 cm}$ mounted on a hemisphere of same radius. The total height of the toy is

$text{15.5 cm}$ . Find the total surface area of the toy.

$text{Sol. :}$

$text{Given :}$

$text{Radius of toy is 3.5 cm}$

$text{height of toy is 15.5 cm}$

$text{To find :}$

$text{The total Surface Area of the toy}$

$text{Solve :}$

$text{Slant height of cone }l = sqrt((h)^2+(r)^2)$

$=sqrt((12)^2+(3.5)^2)$

$=sqrt((144 + 12.25)$

$=sqrt(156.25)$

$text{= 12.5 cm}$

$text{Total SA of the toy}$

$text{= SA of Cone + SA of hemisphere}$

$= pirl + 2pir^2$

$= pir(l + 2r)$

$= 22/7 times 3.5(12.5 + 2times3.5)$

$= 11(12.5 + 7)$

$= 11 times 19.5$

$= 214.5 cm^2$

$text{Answer :}$

$text{Total SA of the toy is 214.5 cm}^2$ .

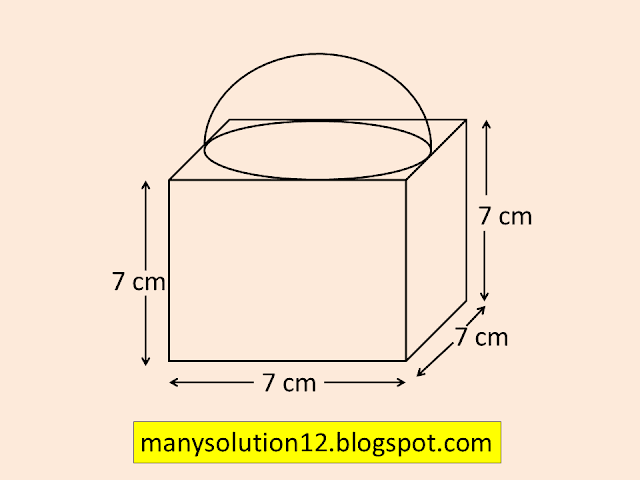
Q4. A cubical block of side

$text{7 cm}$ is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.

$text{Sol. :}$

$text{Given :}$

$text{Side of Cubical block = 7 cm}$

$text{To find :}$

$text{The Surface Area of the solid}$

$text{Solve :}$

$text{Diameter of sphere d = 7cm}$

$text{Radius of sphere r = }7/2 text{ cm}$

$text{Total S A of solid}$

$text{= T S A of the Cube + C S A of the hemisphere}$

$text{ - base area of hemisphere}$

$= 6a^2 + 2pir^2 - pir^2$

$= 6a^2 + pir^2$

$= 6 times (7)^2 + 22/7 times(7/2)^2$

$= 6 times 49 + 22/7 times 7/2 times 7/2$

$= 294 + 11 times 7/2$

$= 294 + 38.5$

$= 332.5 text{cm}^2$

$text{Answer :}$

$text{ T S A of solid is 332.5 cm}^2.$

Q5. A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter $text{l}$ of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.

$text{Sol. :}$

$text{Given :}$

$text{Let the Side of the Cube } a = l$

$text{Let the diameter of the hemispherical bore } d = l$

$text{Radius of the hemisphere bore } r = l/2$

$text{To find :}$

$text{Surface Area of the remaining solid}$

$text{Solve :}$

$text{Surface Area of the remaining solid}$

$text{= Total S A of cube + C S A of the hemisphere}$

$text{ - Area of the circular base}$

$= 6l^2 + 2pir^2 - pir^2$

$= 6l^2 + pir^2$

$= 6l^2 + pi(l/2)^2$

$= (24l^2 + pil^2)/4$

$= l^2/4(24 + pi)$

$text{Answer}$

$text{Surface Area of remaining solid }l^2/4(24 + pi).$

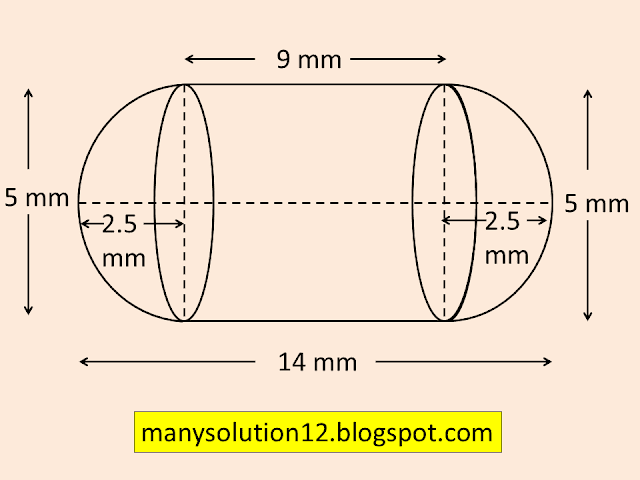
Q6. A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (see figure). The length of the entire capsule is

$text{14 mm}$ and the diameter of the capsule is

$text{5 mm}$ . Find its surface area.

$text{Sol. :}$

$text{Given :}$

$text{Length of the entire capsule is 14 mm}$

$text{Diamter of hemisphere & cylinder }d = 5 text{mm}$

$text{Radius of hemisphere & cylinder }r = 5/2 text{mm}$

$text{To find :}$

$text{Surface Area of the capsule}$ .

$text{Solve :}$

$text{Length of the capsule = length of the cylinder }(l)$

$text{ + 2}times text{radius of the hemisphere}$

$14 = l + 5$

$l = 14 - 5$

$l = 9$

$text{S A of capsule = C S A Cylinder }$

$text{ + 2 (C S A of hemisphere)}$

$text{S A of capsule} = 2pirl + 2 times 2pir^2$

$text{S A of capsule} = 2pir(l + 2r)$

$text{S A of capsule} = 2times22/7times5/2(9 + 2times5/2)$

$text{S A of capsule} = 110/7(14)$

$text{S A of capsule} = 220 text{ mm}^2$

$text{Answer :}$

$text{S A of capsule is 220 mm}^2$ .

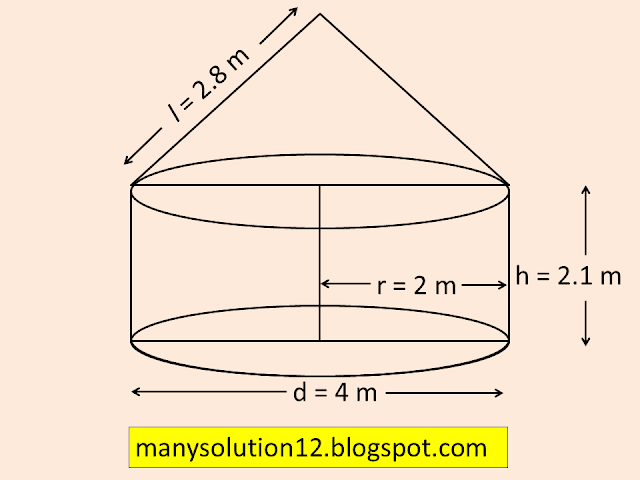
Q7. A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are

$text{2.1 m}$ and

$text{4 m}$ respectively, and the slant height of the top is

$text{2.8 m,}$ find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of

$text{500 per m}^2$ . ( Note that the base of the tent will not be covered with canvas.)

$text{Sol. :}$

$text{Given :}$

$text{Height of Cylinder part of tent }h = 2.1text{ m}$

$text{Diameter of Cylinder & Cone part }d = 4text{ m}$

$text{Radius of Cylinder & Cone part }r = 2text{ m}$

$text{Slant height of Cone part }l = 2.8text{ m}$

$text{To find :}$

$text{Find the area of the canvas used for making a tent.}$

$text{Find the cost of the canvas of the tent}$

$text{Solve :}$

$text{Area of canvas = C S A of Cylinder}$

$text{ + C S A of Cone}$

$text{Area of canvas} = 2pirh + pirl$

$text{Area of canvas} = pir(2h + l)$

$text{Area of canvas} = 22/7times2(2times2.1 + 2.8)$

$text{Area of canvas} = 44/7times(4.2 + 2.8)$

$text{Area of canvas} = 44/7times 7.0$

$text{Area of canvas} = 44.0 text{m}^2$

$text{cost of the canvas = Area}times text{Rate}$

$text{ = 44}times text{₹ 500}$

$text{ = ₹ 22000}$

$text{Answer :}$

$text{Area of canvas 44 m}^2, text{and cost ₹ 22000}$

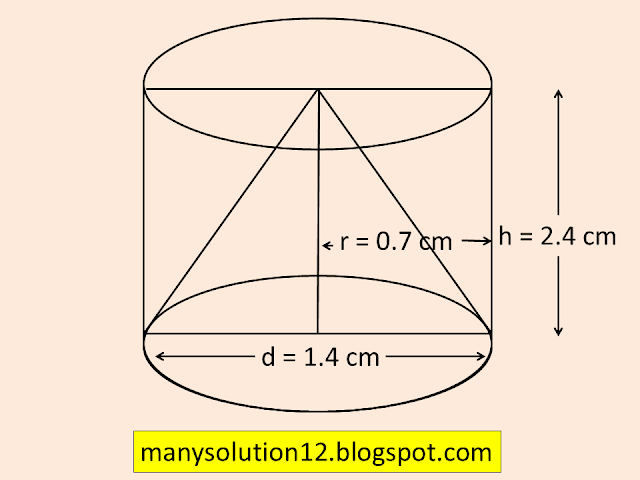
Q8. From a solid cylinder whose height is

$text{2.4 cm}$ and diameter

$text{1.4 cm,}$ a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest

$text{cm}^2$ .

$text{Sol. :}$

$text{Given:}$

$text{Height of Cylinder }h = 2.4 text{ cm}$

$text{Diameter }d = 1.4 text{ cm}$

$text{Radius } r = 1.4/2 = 0.7 text{cm}$

$text{To find :}$

$text{The total Surface Area of the remaining solid}$

$text{Solve :}$

$text{slant height } l = sqrt((h)^2 + (r)^2)$

$l = sqrt((2.4)^2 + (0.7)^2)$

$l = sqrt(5.76 + 0.49)$

$l = sqrt(6.25)$

$l = 2.5 text{cm}$

$text{T S A of remaining solid = S A of Cylinder}$

$text{ + S A of cone + area of base}$

$text{ = } 2pirh + pirl + pir^2$

$text{ = } pir(2h + l + r)$

$text{ = } 22/7times0.7(2times2.4 + 2.5 + 0.7)$

$text{ = } 2.2(4.8 + 3.2)$

$text{ = } 2.2(8)$

$text{ = } 17.6 text{ cm}^2$

$text{ = } 18 text{ cm}^2$

$text{Answer :}$

$text{T S A of remaining solid 18 cm}^2$ .

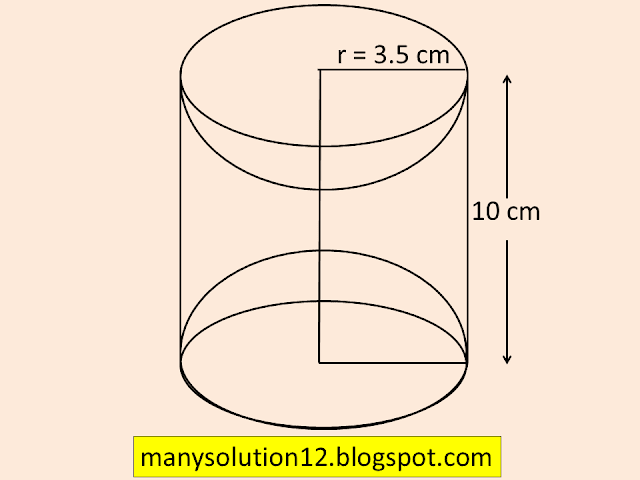
Q9. A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Figure. If the height of the cylinder is

$text{10 cm}$ , and its base is of radius

$text{3.5 cm,}$ find the total surface area of the article.

$text{Sol. :}$

$text{Given :}$

$text{Height of the Cylinder } h = 10 text{ cm}$

$text{Radius of the base} r = 3.5 text{ cm}$

$text{To find :}$

$text{The total surface area of the artical}$

$text{Solve :}$

$text{T S A of the article = C S A of Cylinder}$

$text{ + 2(C S A of hemisphere)}$

$text{ = }2pirh + 2times2pir^2$

$text{ = }2pir(h + 2r)$

$text{ = }2times22/7times3.5(10 + 2times3.5)$

$text{ = }22 times 17$

$text{ = }374 text{cm}^2$

$text{Answer :}$

$text{T S A of the article is 374 cm}^2$ .

Comments

Anonymous said…

Very good

19 December 2021 at 22:22

Search This Blog

10th Maths 13.1

NCERT Class 10th solution of Exercise 13.2

NCERT Class 10th solution of Exercise 13.3

NCERT Class 10th Maths Projects

Exercise 13.1

Comments

Popular posts from this blog

10th Maths Chapter 1

CBSE 10th and 12th Result

RSKMP 5th & 8th Result