10th Maths 6.5
NCERT Class 10th solution of Exercise 6.1
NCERT Class 10th solution of Exercise 6.2
NCERT Class 10th solution of Exercise 6.3
NCERT Class 10th solution of Exercise 6.4
Exercise 6.5
Q1. Sides of triangles are given below. Determine which of them are right triangles In case of a triangle, write the length of its hypotenuse.
i) `7cm, 24cm, 25cm`
ii) `3cm, 8cm, 6cm`
iii) `50cm, 80cm, 100cm`
iv) `13cm, 12cm, 5cm`.
Sol. :
i) We use Pythagoras Theorem
`(25)^2=(24)^2+(7)^2`
`625=576+49`
`625=625`
So, it is a right triangle with hypotenuse is `25`.
Answer: Yes, `25`.
ii) We use Pythagoras Theorem
`(8)^2=(6)^2+(3)^2`
`64=36+9`
`64≠45`
No, it is not a right triangle.
Answer: No.
iii) We use Pythagoras Theorem
`(100)^2=(80)^2+(50)^2`
`10000=6400+2500`
`10000≠8900`
No, it is not a right triangle.
Answer: No.
iv) We use Pythagoras Theorem
`(13)^2=(12)^2+(5)^2`
`169=144+25`
`169=169`
Yes, it is a right triangle with hypotenuse is `13`
Answer: Yes, `13`.
Q2. `PQR` is a triangle right angled at `P` and `M` is a point on `QR` such that `PM⊥QR`. Show that `PM^2=QM.MR`.
Sol. :
`PQR` is a triangle right angled at `p`.
`PM⊥QR`
To Prove:
`PM^2=QM.MR`
Proof:
If a perpendicular is drawn from the vertex of the right angle of a right triangle to hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle and to each other.
`triangle PMR∼triangle QMR`
`(PM)/(QM)=(MR)/(PM)`
`PM^2=QM.MR`
Proved.
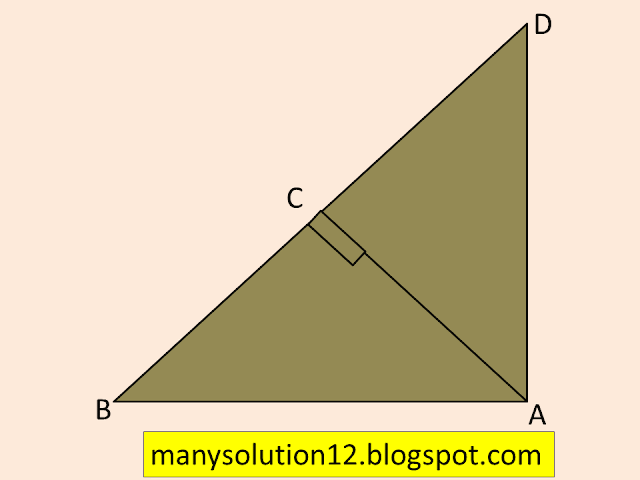
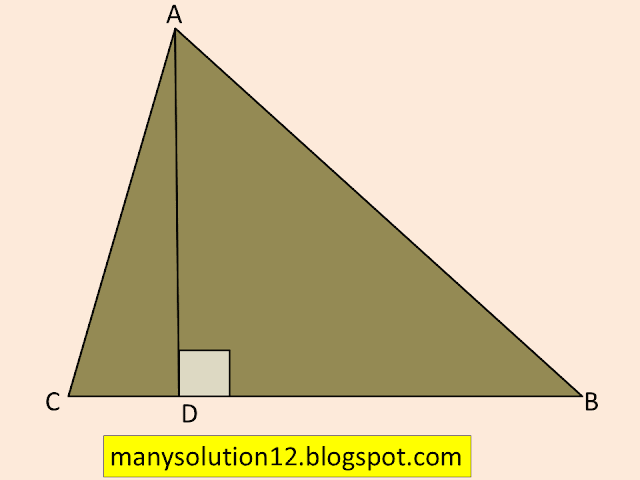
Q3. In figure, `ABD` is a triangle right angled at `A` and `AC⊥BD`. Show that
i) `AB^2=BC.BD`
ii) `AC^2=BC.DC`
iii) `AD^2=BD.CD`
Given:
`ABD` is a triangle right angled at `A` and `AC⊥BD`.
To Prove:
i) `AB^2=BC.BD`
ii) `AC^2=BC.DC`
iii) `AD^2=BD.CD`
Proof:
If a perpendicular is drawn from the vertex of the right angle of a right triangle to hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle and to each other.
i) `triangleACB∼triangleBAD` [ By Theorem 6.7]
`(AB)/(BD)=(BC)/(AB)` [Sides are proportional]
`AB^2=BC.BD`
Proved.
ii) `triangleACB∼triangleACD` [ By Theorem 6.7]
`(AC)/(CD)=(BC)/(AC)` [Sides are proportional]
`AC^2=BC.BD`
Proved
iii) `triangleDCA∼triangleDAB` [ By Theroem 6.7]
`(AD)/(BD)=(CD)/(AD)` [ Side are proportional]
`AD^2=BD.CD`
Proved.
Q4. `ABC` is an isosceles triangle right angled at `C`. Prove that `AB^2=2AC^2`.
Sol. :
`ABC` is an isosceles `triangle` right-angled at `C`.
To prove:
`AB^2=2AC^2`
Proof:
In `triangle ABC`
By Pythagoras theorem
`AB^2=BC^2+AC^2`
`triangle ABC` is an isosceles, So that `AC=BC`
`AB^2=AC^2+AC^2`
`AB^2=2AC^2`
Proved.
Q5. `ABC` is an isosceles triangle with `AC=BC`. If `AB^2=2AC^2`, prove that `ABC` is a right triangle.
Sol. :
`triangle ABC, AC=BC`
`AB^2=2AC^2`
To Prove:
`ABC` is a right.
Proof:
In `triangle ABC`
`AB^2=2AC^2`
`AB^2=AC^2+AC^2`
`AB^2=BC^2+AC^2`[`AC=BC`]
`angleACB=90^circ` [By converse of Pythagoras theorem]
This gives
The given `triangle ABC` is a triangle right angled at `C`.
Proved.
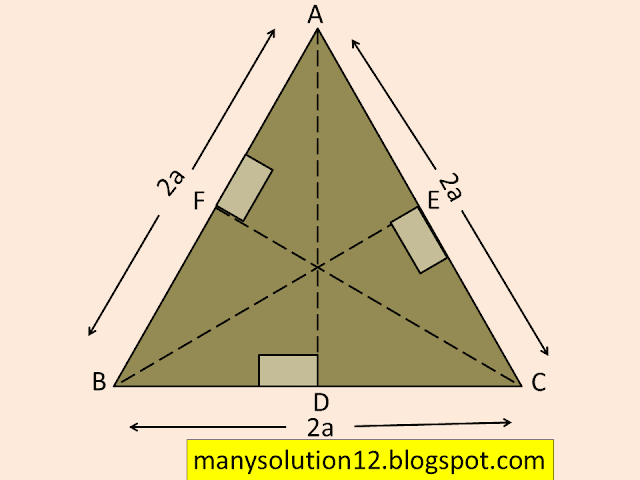
Q6. `ABC` is an equilateral triangle of side `2a`. Find each of its altitudes.
Sol. :
`ABC` is an equilateral `triangle`.
`AB=BC=CA=2a`.
To Find:
Each its altitudes.
Solve:
In equilateral `triangle`
`AD=BE=CF`____(1) [Altitudes of equilateral `triangle`]
`BD=1/2BC` [Altitudes of equilateral `triangle`]
`BD=1/2times2a=a`____(2)
`AD^2=AB^2-BD^2`___(3) [By Pythagoras theorem]
`AD^2=(2a)^2-(a)^2` [From equations (1), (2) and (3)]
`AD^2=4a^2-a^2`
`AD^2=3a^2`________(4)
`AD=BE=CF=asqrt3` [By equation (1) and (4)]
Answer:
The length of each altitude of equilateral `triangle` is `asqrt3`.
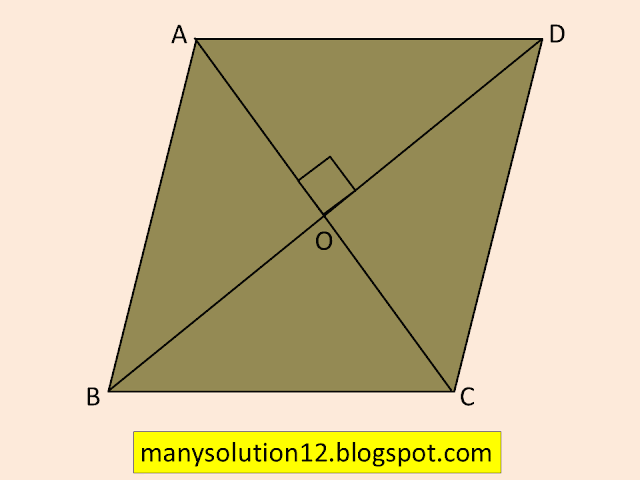
Q7. Prove that the sum of the squares of the side of a rhombus is equal to the sum of the squares of its diagonals.
Sol. :
rhombus, its diagonals.
To Prove:
`AB^2+BC^2+CD^2+DA^2=AC^2+BD^2`
Proof:
Let `ABCD` is rhombus with diagonal `AC` and `BD`
`AB=BC=CD=DA=x`___(1) [Sides of rhombus]
`angleAOB=angleBOC=angleCOD=angleDOA=90^circ`
[Diagonal of rhombus bisect each other at right angle]
`OA=OC=1/2AC`
`OB=OD=1/2BD`
In right `triangleAOB`
`AB^2=OA^2+OB^2` [ By Pythagorus theorem]
`x^2=((AC)/2)^2+((BD)/2)^2`
`x^2=(AC)^2/4+(BD)^2/4`
`4x^2=AC^2+BD^2`________(2)
`AB^2+BC^2+CD^2+DA^2=4x^2`_____(3)
[From equation (1)]
`AB^2+BC^2+CD^2+DA^2=AC^2+BD^2`
[By equation (2)&(3)]
Proved.
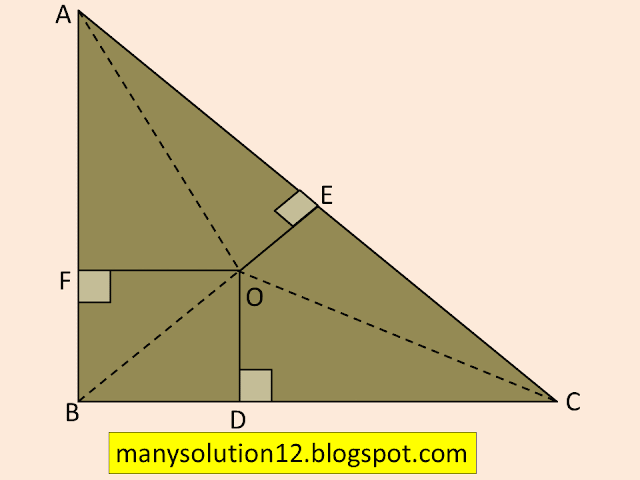
Q8. In figure, `O` is a point in the interior of a triangle `ABC`, `OD⊥BC,OE⊥AC` and `OF⊥AB`. Show that
i) `OA^2+OB^2+OC^2-OD^2-OE^2-OF^2=AF^2+BD^2+CE^2`,
ii) `AF^2+BD^2+CE^2=AE^2+CD^2+BF^2`.
Given:
`triangle ABC`, `O` is interior
`OD⊥BC, OE⊥AC, OF⊥AB`
Construction:
Join `OA, OB,` and `OC`
Proof:
i) In right `triangle OFA`
`OA^2-OF^2=AF^2`____(1)
[By Pythagoras theorem]
In right `triangle OBD`
`OB^2-OD^2=BD^2`____(2)
[By Pythagoras theorem]
In right `triangleOEC`
`OC^2-OE^2=CE^2`____(3)
[By Pythagoras theorem]
By equation (1)+(2)+(3)
`OA^2-OF^2+OB^2-OD^2+OC^2-OE^2=AF^2+BD^2+CE^2`
`OA^2+OB^2+OC^2-OF^2-OD^2-OE^2=AF^2+BD^2+CE^2`___(4)
Proved.
ii)
In right `triangle OEA`
`OA^2-OE^2=AE^2`____(5)
[By Pythagoras theorem]
In right `triangle OFB`
`OC^2-OD^2=BF^2`____(6)
[By Pythagoras theorem]
In right `triangle ODC`
`OC^2-OD^2=CD^2`____(7)
By equation (5)+(6)+(7)
`OA^2-OE^2+OB^2-OF^2+OC^2-OD^2=AE^2+BF^2+CD^2`___(8)
`AF^2+BD^2+CE^2=AE^2+CD^2+BF^2`
[By equation (4), (8)]
Proved.
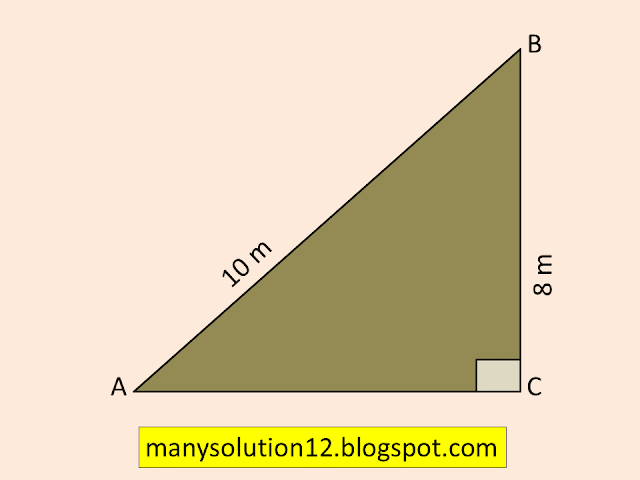
Q9. A ladder `10m` long reaches a window `8m` above the ground. Find the distance of the foot of the ladder from base of the wall.
Sol. :
Length of ladder `10 m`, the height of the window `8 m`
To find:
The distance of the foot of the ladder from the base of the wall.
Solve:
In right `triangle ABC`
By Pythagoras theorem
`AC^2=AB^2-BC^2`
`AC^2=(10)^2-(8)^2`
`AC^2=100-64`
`AC^2=36`
`AC^2=(6)^2`
`AC=6`
Answer:
The distance of the foot of the ladder from the base of the wall is `6 m`.
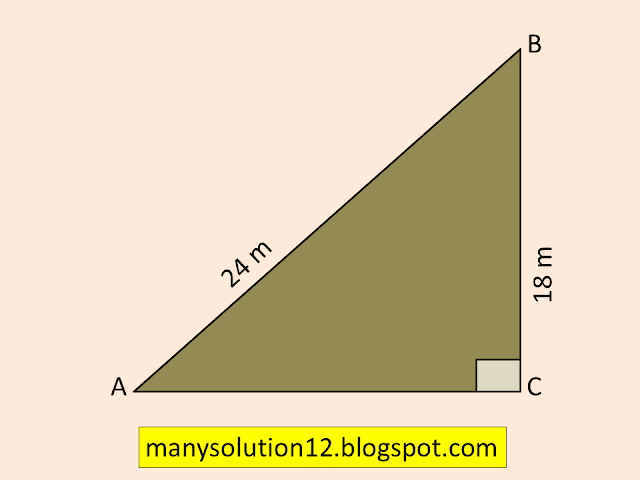
Q10. A guy wire attached to a vertical pole of height `18m` is `24m` long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Sol. :
Length of vertical pole `18 m`
length of wire `24 m`
To find:
The distance from the base of the pole should be the stake.
Solve:
In right `triangle ABC`
By Pythagoras theorem
`AC^2= AB^2-BC^2`
`AC^2=(24)^2-(18)^2`
`AC^2=576-324`
`AC^2=252`
`AC^2=(6sqrt7)^2`
`AC=6sqrt7 m`
Answer:
The distance from the base of the pole should the stake is `6sqrt7 m`.
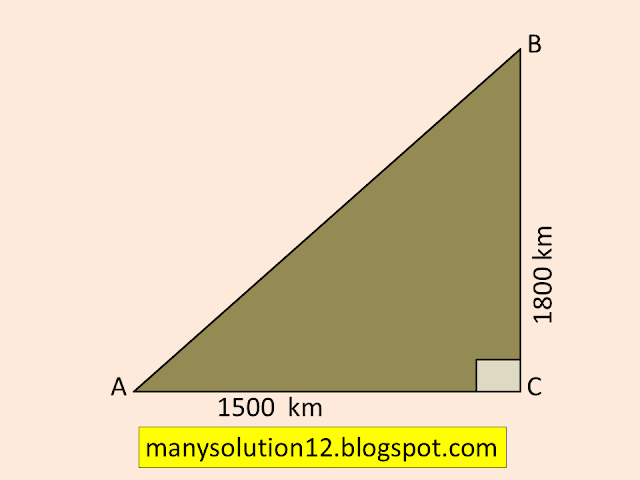
Q11. An aeroplane leaves an airport and flies due north at a speed of `1000km` per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of `1200km` per hour. How far apart will be the two planes after `1(1)/2` hours?
Sol. :
Speed of first aeroplane `1000 km` per hour
Speed of second aeroplane `1200 km` per hour
Time `1(1)/2` hour.
To find:
The distance of two planes after `1(1)/2` hour.
Solve:
First aeroplane cover after `1(1)/2=3/2` hour
distance `=speed times time`
`=1000times3/2=1500 km`
Second aeroplane cover after `1(1)/2=3/2` hour
distance `=speed times time`
`=1200times3/2=1800 km`
In right `triangle ABC`
By Pythagoras theorem
`AB^2=AC^2+BC^2`
`AB^2=(1500)^2+(1800)^2`
`AB^2=2250000+3240000`
`AB^2=5490000`
`AB^2=(300sqrt61)^2`
`AB=300sqrt61 km`
Answer:
The distance of two plans after `1(1)/2` hour is `300sqrt61 km`.
Q12. Two poles of heights `6m` and `11m` stand on a plane ground. If the distance between the feet of the poles is `12m`, find the distance between their tops.
Sol. :
Height of poles `6m, 11m`
Distance between poles `12m`
To find:
Distance between their tops.
Construction:
Draw `AE⊥CD`
`AE=BD=12m`
`ED=AB=6m`
`CE=5m`
Solve:
In right `triangle AEC`
By Pythagoras theorem
`AC^2=AE^2+CE^2`
`AC^2=(12)^2+(5)^2`
`AC^2=144+25`
`AC^2=169`
`AC^2=(13)^2`
`AC=13 m`
Answer:
The distance between the top of the poles is `13 m`.
Q13. `D` and `E` are points on the sides `CA` and `CB` respectively of a triangle `ABC` right angled at `C`. Prove that `AE^2+BD^2=AB^2+DE^2`.
Sol. :
`triangle ABC, angleA=90^circ,`
`D,` and `E` are points on `AC` and `BC`.
Construction:
Join `DE, BD,` and `AE`.
To Prove:
`AE^2+BD^2=AB^2+DE^2`
Proof:
In right `triangle ACE`
By Pythagoras theorem
`AE^2=AC^2+EC^2`______(1)
In right `triangle BCD`
By Pythagoras theorem
`BD^2=BC^2+DC^2`______(2)
We add equations (1) and (2)
`AE^2+BD^2=AC^2+EC^2+BC^2+DC^2`___(3)
In right `triangle ACB`
By Pythagoras theorem
`AB^2=AC^2+BC^2`_______(4)
In right `triangle DCE`
By Pythagoras theorem
`DE^2=DC^2+EC^2`_______(5)
We add equation (4) and (5)
`AB^2+DE^2=AC^2+BC^2+DC^2+EC^2`____(6)
from equations (3) and (6)
`AE^2+BD^2=AB^2+DE^2`
Proved.
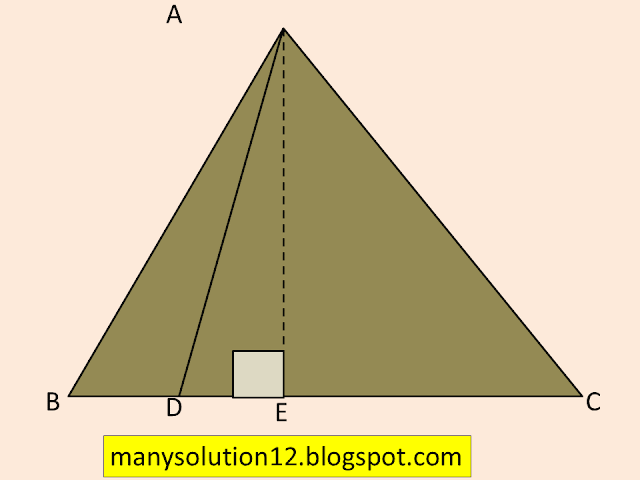
Q14. The perpendicular from `A` on side `BC` of a `triangleABC` intersects `BC` at `D` such that `DB=3CD` (see figure). Prove that `2AB^2=2AC^2+BC^2`.
Given:
`triangle ABC,` `AD⊥BC` `DB=3CD`
`DB=3/4BC`
`CD=1/4BC`______(1)
To Prove:
`2AB^2=2AC^2+BC^2`
Proof:
In right `triangle ABD`
By Pythagoras theorem
`AB^2 =AD^2+BD^2`___(2)
In right `triangle ADC`
By Pythagoras theorem
`AC^2=AD^2+CD^2`____(3)
From equations (2) - (3)
`AB^2-AC^2=AD^2+BD^2-AD^2-CD^2`
`AB^2-AC^2=BD^2-CD^2`
`AB^2-AC^2=(BD+CD)(BD-CD)`
`AB^2-AC^2=(3/4BC+1/4BC)(3/4BC-1/4BC)`
`AB^2-AC^2=BCtimes1/2BC`
`AB^2-AC^2=1/2BC^2`
`2AB^2-2AC^2=BC^2`
`2AB^2=2AC^2+BC^2`.
Proved.
Q15. In an equilateral triangle `ABC, D` is a point on side `BC` such that `BD=1/3BC`. Prove that `9AD^2=7AB^2`.
Sol. :
Given:
Equilateral `triangle ABC`, `D` is on side `BC`
such that `BD=1/3BC`
Construction:
Draw `AE⊥BC`
Proof:
`AB=BC=CA`_____(1)
(Sides of equilateral `triangle`)
`BD=1/3BC`____(2) (Given)
`BE=EC=1/2BC=AB/2`___(3)
(Altitude `AE` of equilateral `triangle` bisects the `BC`)
`DE=BE-BD`
`DE=(BC)/2-(BC)/3`__(4)[From eq. (2),(3)]
`DE=(3BC-2BC)/6`
`DE=(BC)/6=(AB)/6`__(5)[From eq.(4), (1)]
In right `triangle AEB`
By Pythagoras theorem
`AE^2=AB^2-BE^2`_____(6)
In right `triangle AED`
By Pythagoras theorem
`AE^2=AD^2-DE^2`_____(7)
`AB^2-BE^2=AD^2-DE^2`___(8)[From eq.(6), (7)]
`AB^2-((AB)/2)^2=AD^2-((AB)/6)^2` [From eq.(8), (3), (5)]
`AB^2-(AB)^2/4=AD^2-(AB)^2/36`
`36AD^2-9AB^2=36AD^2-AB^2`
`36AD^2=36AB^2+AB^2-9AB^2`
`36AD^2=28AB^2`
`9AD^2=7AB^2`
Proved.
Q16. In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Sol. :
Let `triangle ABC` an equilateral, `AD` is altitude.
To Prove:
`3AB^2=4AD^2`
Proof:
In `triangle ABC`
`BD=CD` [`D` bisect `BC`]
`1/2BC=1/2AB`__(1) [`AB=BC=CA`]
In right `triangle ADB`
By Pythagoras theorem
`AB^2=AD^2+BD^2`__(2)
`AB^2=AD^2+((AB)/2)^2`
`AB^2=AD^2+(AB)^2/4`
`4AB^2=AD^2+AB^2
`3AB^2=4AD^2`
Proved.
Q17. Tick the correct answer and justify: In `triangleABC`, `AB=6sqrt3cm` and `BC=6cm`.
The angle `B` is:
A) `120^circ`
B) `60^circ`
C) `90^circ`
D) `45^circ`
Sol. :
`AB^2+BC^2=AC^2` [By Pythagoras theorem]
`(6sqrt3)^2+(6)^2=(12)^2`
`108+36=144`
`144=144`
So that `angleB=90^circ`.
Answer:
(c) `90^circ`






Comments