10th Maths 6.2

Exercise 6.2

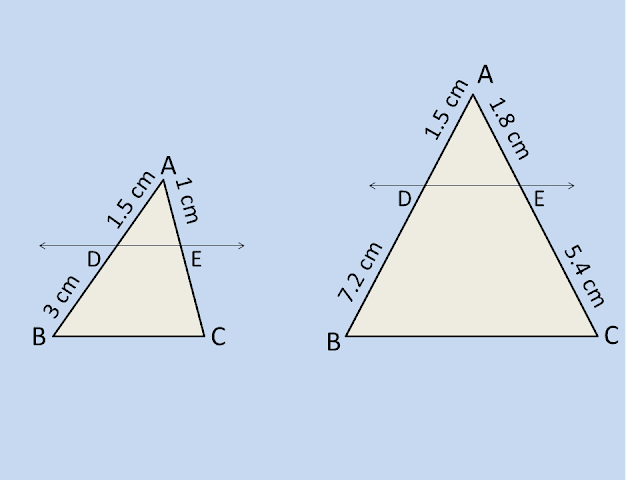
Q1. In the figure i) and ii)

$DE∥BC.$ Find the

$EC$ in (i) and

$AD$ in (ii).

Sol.

i) Given

$DE∥BC$

$(AD)/(DE)=(AE)/(EC)$

$(1.5)/3=1/(EC)$

$EC=3/(1.5)=2$ cm.

Answer :

$EC=2$ cm.

ii) Given

$DE∥BC$

$(AD)/(DE)=(AE)/(EC)$

$(AD)/(7.2)=(1.8)/(5.4)$

$AD=(1.8)/(5.4)times7.2$

$AD=2.4$ cm.

Answer :

$AD=2.4$ cm.

Q2.

$E$ and

$F$ are points on the sides

$PO$ and

$PR$ respectively of a

$triangle PQR.$ For each of the following cases, state whether

$EF∥QR$ :

$PE=3.9$ cm,

$EQ=3$ cm,

$PF=3.6$ cm and

$FR=2.4$ cm

ii)

$PE=4$ cm,

$QE=4.5$ cm,

$PF=8$ cm, and

$RF=9$ cm

iii)

$PQ=1.28$ cm,

$PR=2.56$ cm,

$PE=0.18$ cm, and

$PF=0.36$ cm.

Sol.

$trianglePQR$

Points

$E$ and

$F$ are on sides

$PQ$ and

$PR$

$(PE)/(EQ)=(3.9)/3$

$(PE)/(EQ)=1.3$

and

$(PF)/(FR)=(3.6)/(2.4)$

$(PF)/(FR)=1.5$

$(PE)/(EQ)ne(PF)/(FR)$

$EF∦QR$

Answer :

$EF∦QR$ .

ii)

$(PE)/(EQ)=(4)/(4.5)$

$(PE)/(EQ)=(8)/(9)$

and

$(PF)/(FR)=(8)/(9)$

$(PE)/(EQ)=(PF)/(FR)$

$EF∥QR$

Answer :

$EF∥QR$ .

iii)

$(PE)/(PQ)=(0.18)/(1.28)$

$(PE)/(PQ)=(18)/(128)=9/(64)$

and

$(PF)/(PR)=(0.36)/(2.56)$

$(PF)/(PR)=(36)/(256)=(9)/(64)$

$(PE)/(PQ)=(PF)/(PR)$

$EF∥QR$

Answer :

$EF∥QR$

Q3. In Figure, if

$LM∥CB$ and

$LN∥CD$ , prove that

$(AM)/(AB)=(AN)/(AD)$

Sol. :

$triangleABC$

Given

$LM∥CB$

$(AM)/(AB)=(AL)/(AC)$ ______________(1)

and in

$triangleACD,$

Given

$LN∥CD$

$(AN)/(AD)=(AL)/(AC)$ ______________(2)

from equation (1) & (2)

$(AM)/(AB)=(AN)/(AD)$

Proved.

Q4. In Figure,

$DE∥AC$ and

$DF∥AE.$ Prove that

$(BF)/(FE)=(BE)/(EC)$

Sol. :

$triangleBAC$

Given

$DE∥AC$

$(BE)/(EC)=(BD)/(DA)$ ____________(1)

and in

$triangleBAE$

Given

$DF∥AE$

$(BE)/(FE)=(BD)/(DA)$ _____________(2)

from equation (1) & (2)

$(BF)/(FE)=(BE)/(EC)$

Proved.

Q5. In Figure,

$DE∥OQ$ and

$DF∥OR.$ Show that

$EF∥QR.$

Sol. :

$trianglePQO$

Given

$DE∥OQ$

$(PE)/(EQ)=(PD)/(DO)$ ____________(1)

and in

$trianglePOR$

Given

$DF∥OR$

$(PF)/(FR)=(PD)/(DO)$ ____________(2)

from equation (1) and (2)

$(PE)/(EQ)=(PF)/(FR)$

So that in

$trianglePQR$

$EF$ divides

$PQ$ and

$PR$ the two sides in same ratio.

then

$EF∥QR$

Proved.

Q6. In Figure,

$A, B,$ and

$C$ are points on

$OP, OQ,$ and

$OR$ respectively such that

$AB∥PQ$ and

$AC∥PR.$ Show that

$BC∥QR.$

Sol. :

$triangleOPQ$

Given

$AB∥PQ$

$(OB)/(BQ)=(OA)/(AP)$ ____________(1)

and in

$triangleOPR$

Given

$AC∥PR$

$(OC)/(CR)=(OA)/(AP)$ ____________(2)

from equation (1) and (2)

$(OB)/(BQ)=(OC)/(CR)$

So that in

$triangleOQR$

$BC$ divides

$OQ$ and

$OR$ the two sides in same ratio.

then

$BC∥QR$

Proved.

Q7. Using Theorem

$6.1$ , prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. ( Recall that you have proved it in Class IX ).

Sol. :

Let

$trianglePQR$ which have a line

$ST∥QR$ is drawn from the point

$S$ , a mid-point of side

$PQ$ .

$ST$ intersect the side

$PR$ at point

$T$ .

Given

$S$ is the mid-point of

$PQ$ .

$PS=SQ$

$(PS)/(SQ)=1$ ____________(1)

and in the

$trianglePQR, ST∥QR$

$(PT)/(TR)=(PS)/(SQ)$ _____(2) (By theroem

$6.1$ )

[Theorem $6.1$ : If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.]

from equation (1) & (2)

$(PT)/(TR)=(PS)/(SQ)$

$(PT)/(TR)=1$

$PT=TR$

$ST$ is the bisector of side

$PR$

So that, in a triangle a line is drawn through the mid-point of one side of the triangle parallel to another side bisect the third side.

Prove.

Q8. Using Theorem

$6.2$ , prove that the line joining the mid-pints of any two sides of a triangle is parallel to the third side. ( Recall that you have done it in Class IX ).

Sol. :

Let

$trianglePQR$ which have

$S$ and

$T$ are mid-points of its sides

$PQ$ and

$PR$ respectively. Line

$ST$ is drawn.

Given

$PS=SQ$ and

$PT=TR$

$(PS)/(SQ)=(PT)/(TR)=1$

Line

$ST$ , divides

$PQ$ and

$PR$ the two sides of

$trianglePQR$ at points

$S$ and

$T$ in the same ratio,

$1:1$ .

$ST∥QR$ (By Theorem

$6.2$ )

[ Theorem $6.2$ : If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.]

So that the line joining the mid-points of any two sides of a triangle is parallel to the third side.

Proved.

Q9.

$ABCD$ is a trapezium in which

$AB∥DC$ and diagonals intersect each other at the point

$O$ . Show that

$(AO)/(BO)=(CO)/(DO)$ .

Sol. :

In trapezium

$ABCD$ which have

$AB∥DC$ and its diagonals

$AC$ and

$BD$ intersect each other at point

$O$ .

Construction: Draw a line

$EF∥AB∥DC$ passing through

$O$ .

$triangleADC$ ,

$EF∥DC$ (By construction)

$(AE)/(ED)=(AO)/(CO)$ _____________(1) (By Theroem

$6.1$ )

[Theorem $6.1$ : If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.]

$triangleBAD$

$EF∥AB$ (By construction)

$(AE)/(ED)=(BO)/(DO)$ _____________(2) (By Theroem

$6.1$ )

from equation (1) and (2)

$(AO)/(CO)=(BO)/(DO)$

$(AO)/(BO)=(CO)/(DO)$

Proved.

Alternate method:

In Trapezium

$ABCD$ ,

$AB∥DC$ and diagonals

$AC$ and

$BD$ intersect each other at a point

$O$ .

Given

$AB∥DC$ and

$AC$ is transversal

$angleOAB=angleOCD$ ___________(1) (Alternate angle)

Given

$AB∥DC$ and

$BD$ is transversal

$angleOBA=angleODC$ ___________(2) (Alternate angle)

$angleAOB=angleCOD$ ___________(3) (Vertiacally opposite angles)

By equation (1), (2) and (3)

$triangleOAB∼triangleOCD$ (By AAA Similarity criterion)

$(BO)/(DO)=(AO)/(CO)$

$(AO)/(BO)=(CO)/(DO)$

Proved.

Q10. The diagonals of a quadrilateral

$ABCD$ intersect each other at the point

$O$ such that

$(AO)/(BO)=(CO)/(DO).$ Show that

$ABCD$ is a trapezium.

Sol. :

In quadrilateral

$ABCD$ diagonal

$AC$ and

$BD$ intersect each other at point

$O$ and

Given

$(AO)/(BO)=(CO)/(DO)$

$triangleOAB$ and

$triangleOCD$ ,

$angleAOB=angleCOD$ (Vertically opposite angles)

Given

$(AO)/(BO)=(CO)/(DO)$

here sides are proportional and including the equal angles.

$triangleOAB∼triangleOCD$ (By

$SAS$ similarity criterion)

$angleOAB=angleOCD$ (Corresponding angles are equal)

By alternate angles

$AB∥DC$

So that, the quadrilateral

$ABCD$ is a trapezium.

Proved.

Search This Blog

10th Maths 6.2

NCERT Class 10th solution of Exercise 6.1

NCERT Class 10th solution of Exercise 6.3

NCERT Class 10th solution of Exercise 6.4

NCERT Class 10th solution of Exercise 6.5

NCERT Class 10th Maths Projects

Exercise 6.2

Comments

Popular posts from this blog

10th Maths Chapter 1

CBSE 10th and 12th Result

RSKMP 5th & 8th Result