10th Maths 6.4
NCERT Class 10th solution of Exercise 6.1
NCERT Class 10th solution of Exercise 6.2
NCERT Class 10th solution of Exercise 6.3
NCERT Class 10th solution of Exercise 6.5
Exercise 6.4
Q1. Let `triangleABC∼triangleDEF` and their areas be, respectively, `64cm^2` and `121cm^2`. If `EF=15.4` cm, find `BC`.
`text{Sol.}`
`text{Given,}`
`triangle text{ABC} ∼ triangle text{DEF}`
`text{so that}`
`(text{AB})/(text{DE}) = (text{BC})/(text{EF}) = (text{CA})/(text{FD})`
`(ar(text{ABC}))/(ar(text{DEF})) = ((text{BC})/(text{EF}))^2`
`64/121 = ((text{BC})/15.4)^2`
`(8/11)^2 = ((text{BC})/15.4)^2`
`text{BC} = (8times15.4)/11`
`text{BC} = 123.2/11`
`text{BC} = 11.2 text{ cm}`
`text{Answer:}`
`text{BC} = 11.2 text{ cm}.`
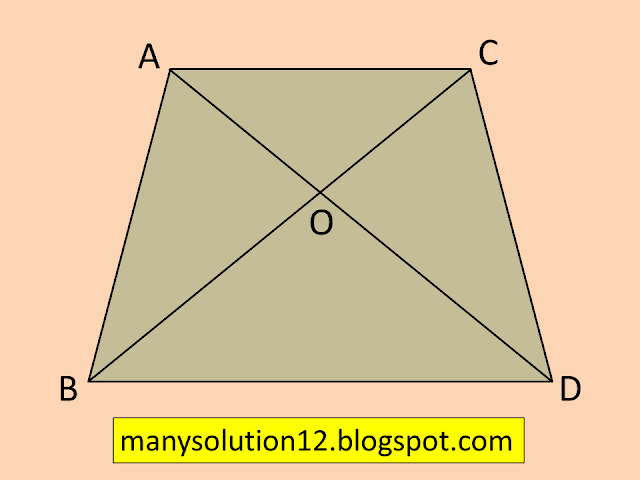
Q2. Diagonals of a trapezium `ABCD` with `AB∥DC` intersect each other at the point `O`. If `AB=2CD`, find the ratio of the areas of triangles `AOB` and `COD`.
`text{Sol.}`
`text{Given,}`
`text{ABCD is trapezium with AB||DC and }``text{AB = 2CD}`
`text{In}triangle text{AOB and}triangle text{COD}`
`angle 1 = angle 2 text{ [Alternate angles]}`
`angle text{AOB = }angle text{COD}text{ [Verticaly opposite angles]}`
`triangle text{AOB}∼triangle text{COD}text{ [By AA]}`
`text{So that}`
`(ar(text{AOB}))/(ar(text{COD})) = ((text{AB})/(text{CD}))^2`
`= ((text{2CD})/(text{CD}))^2`
`= 4/1`
`= 4:1`
`text{Anser:}`
`text{ar(AOB) : ar(COD) = 4:1}`
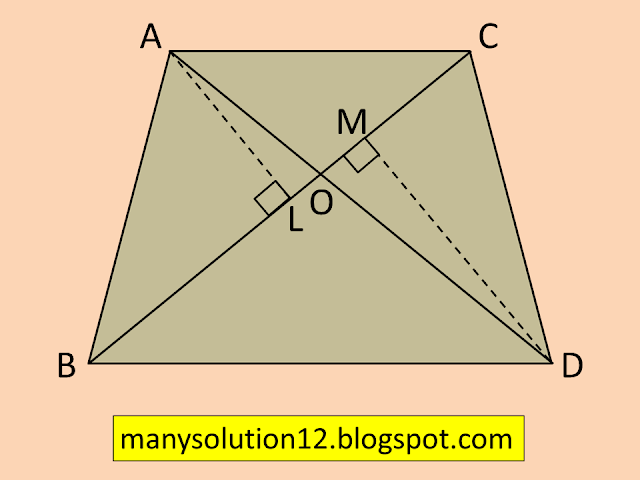
Q3. In Figure, `ABC` and `DBC` are two triangles on the same base `BC`. If `AD` intersects `BC` at `O`, Show that `(ar(ABC))/(ar(DBC))=(AO)/(DO).`
`text{Sol.}`
`text{Given,}`
`triangle text{ABC and }triangle text{DBC on the same base BC }``text{and AD intersects BC at O}`
`(ar(text{ABC}))/(ar(text{DBC})) =(1/2timestext{BC}timestext{AL})/(1/2timestext{BC}timestext{DM})`
`(text{AO})/(text{DO})= (text{AL})/(text{DM})`______(1)
`text{In}triangle text{ALO and } triangle text{DMO}`
`angle text{ALO}=angle text{DMO}=90^circ``[text{AL}⊥text{BC},text{DM}⊥text{BC}]`
`angle text{AOL}=angle text{DOM}``text{[Vertically opposite angles]}`
`triangle text{ALO} ∼ triangle text{DMO}``text{ [By AA]}`
`text{So that}`
`(text{AO})/(text{DO}) = (text{AL})/(text{DM})``[text{from (1)]}`
`text{Proved}`
Q4. If the area of two similar triangles are equal, prove that they are congruent.
`text{Sol.}`
`text{Given}`
`triangle text{ABC}∼triangle text{PQR}`
`text{and}`
`ar (text{ABC})=ar (text{PQR})`
`text{To Prove:}``triangle text{ABC}cong triangle text{PQR}`
`text{Proof:}`
`(ar (text{ABC}))/(ar (text{PQR})) = ((text{AB})/(text{PQ}))^2 =((text{BC})/(text{QR}))^2=((text{CA})/(text{RP}))^2`
`(ar (text{ABC}))/(ar (text{ABC})) = ((text{AB})/(text{PQ}))^2 =((text{BC})/(text{QR}))^2=((text{CA})/(text{RP}))^2`
`1 = ((text{AB})/(text{PQ}))^2 =((text{BC})/(text{QR}))^2=((text{CA})/(text{RP}))^2`
`(text{AB})=(text{PQ})`
`(text{BC})=(text{QR})`
`(text{CA})=(text{RP})`
`triangle text{ABC}cong triangle text{PQR}``text{ [By SSS}]`
`text{Proved}`
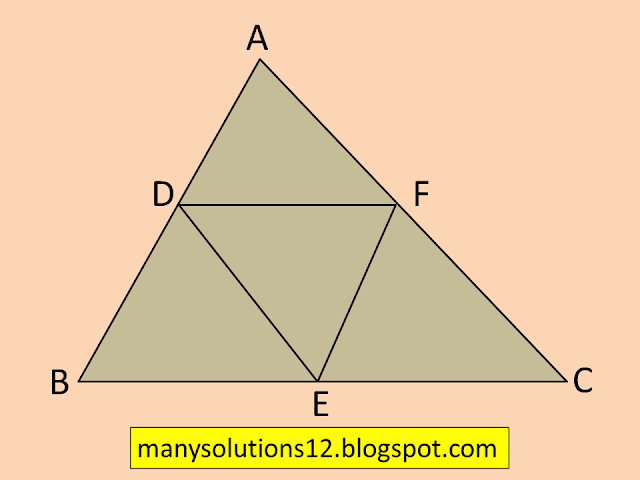
Q5. `D, E` and `F` are respectively the mid-points of sides `AB, BC` and `CA` of `triangle ABC.` Find the ratio of the area of `triangle DEF` and `triangle ABC`.
`text{Sol.}`
`text{In }triangle text{ABC},``text{D, E, and F are mid-points }``text{of sides AB, BC and CA respectively}`
`text{DF}=1/2text{BC}``text{ [By Midpoint Theorem]}`
`text{DE}=1/2text{AC}``text{ [By Midpoint Theorem]}`
`text{EF}=1/2text{AB}``text{ [By Midpoint Theorem]}`
`(text{DF})/(text{BC})=(text{DE})/(text{AC})=(text{EF})/(text{AB})=1/2`
`text{Therefore}`
`triangle text{ABC}∼triangle text{DEF}``text{ [By SSS]}`
`text{And}`
`(ar(text{ABC}))/(ar(text{DEF}))=((text{DF})/(text{BC}))^2`
`(ar(text{ABC}))/(ar(text{DEF}))=(1/2)^2`
`ar(text{ABC}):ar(text{DEF})=1:4`
`text{Answer:}`
`ar(text{ABC}):ar(text{DEF})=1:4`
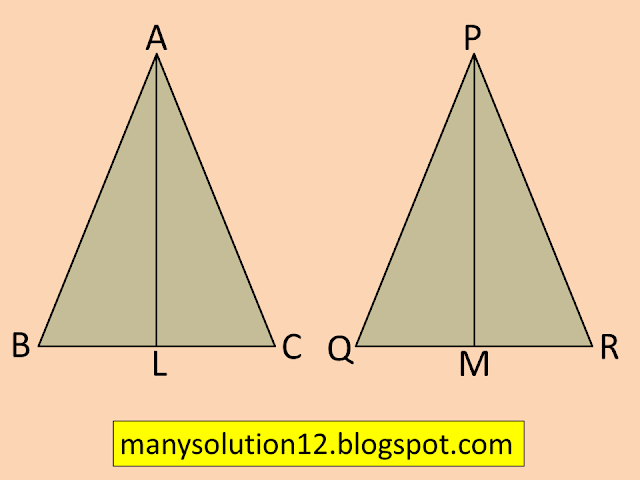
Q6. Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
`text{Sol.}`
`text{Given}`
`triangle text{ABC}∼triangle text{PQR}`
`text{AL and PM are medians}`
`text{To Prove}`
`(ar(text{ABC}))/(ar (text{PQR})) = ((text{AL})/(text{PM}))^2`
`text{Proof}`
`text{In}triangle text{ABC and }triangle text{PQR}`
`(ar (text{ABC}))/(ar (text{PQR})) = ((text{AB})/(text{PQ}))^2`
`triangle text{ABC}∼triangle text{PQR}`
`(text{AB})/(text{PQ})=(text{BC})/(text{QR})=(text{2BL})/(text{2QM})`
`(text{AB})/(text{PQ})=(text{BL})/(text{QM})`____(1)
`angle text{B}=angle text{Q}``[text{angle oppsite to equal side}]`
`triangle text{ABL}∼triangle text{PQM}`
`(text{BL})/(text{QM})=(text{AL})/(text{PM})`____(2)
`text{from equation (1) and (2)}`
`(text{AB})/(text{PQ})=(text{AL})/(text{PM})`
`(ar (text{ABC}))/(ar (text{PQR})) = ((text{AL})/(text{PM}))^2`
`text{Proved}`
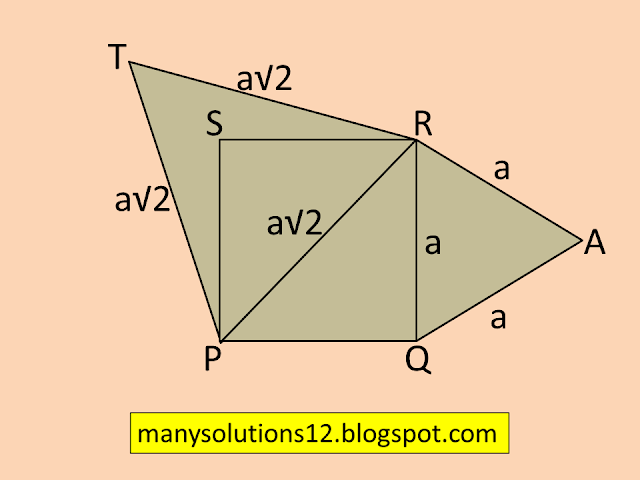
Q7. Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
text{Sol.}`
`text{Let PQRS is a square of side length a.}`
`text{and diagonal PR }asqrt2`
`triangle text{QAR}=triangle text{PRT are equilateral triangles, }``text{so these are similar}`
`(ar(text{QAR}))/(ar(text{PRT}))=((text{QR})/(text{PR}))^2`
`=a^2/(asqrt2)^2`
`=a^2/(2a^2)`
`=1/2`
`ar(text{QAR})=1/2ar(text{PRT})`
`text{Proved}.`
Tick the correct answer and justify:
Q8.`ABC` and `BDE` are two equilateral triangles such that `D` is the mid-point of `BC`. Ratio of the areas of triangles `ABC` and `BDE` is
A) `2:1`
B) `1:2`
C) `4:1`
D) `1:4`
`text{Answer:}`
C) `4:1`
`text{Justifiction}`
`text{Let Sides of equilateral triangles }``text{AB=BC=CA=a}`
`text{D is mid point of BC}`
`text{DB}=1/2a`
`triangle(text{ABC})∼triangle(text{BDE})`
`(ar(text{ABC}))/(ar(text{BDE}))=((text{BC})/(text{BD}))^2`
`=a^2/(1/2a)^2`
`=a^2/(1/4a^2)`
`=4/1`
`=4:1`
Q9. Sides of two similar triangles are in the ratio `4:9`. Areas of these triangles are in the ratio
A) `2:3`
B) `4:9`
C) `81:16`
D) `16:81`
`text{Answer:}`
D) `16:81`
`text{Justification}`
`text{Ratio of area of triangles = }(4/9)^2=16/81`




Comments