9th Maths 9.3
NCERT Class 9th solution of Exercise 9.1
NCERT Class 9th solution of Exercise 9.2
NCERT Class 9th solution of Exercise 10.1
Exercise 9.3
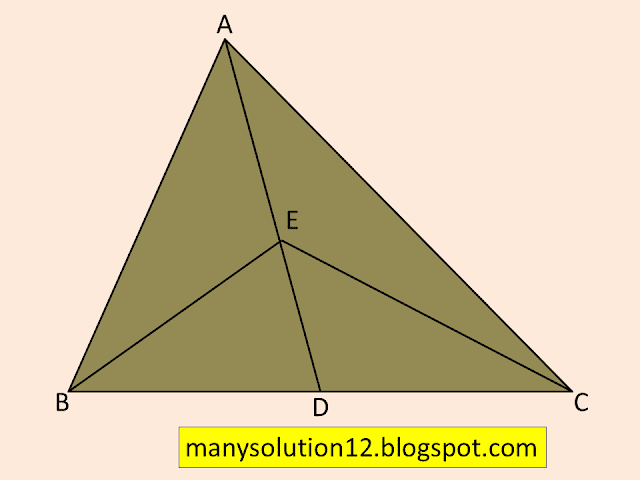
Q1. In Figur, `E` is any point on median `AD` of a `triangleABC.` Show that `ar(ABC)=ar(ACE).`
Given:
`triangleABC`, `AD` is a median.
To Prove:
`ar(ABE)=ar(ACE)`.
Proof:
In `triangleABC`,
`AD` is median
`ar(ABE)=ar(ACE)`__________(1)
In `triangleEBC`,
`ED` is median.
`ar(BDE)=ar(CDE)`__________(2)
By equation (1) - (2)
`ar(ABE)-ar(BDE)=ar(ACE)-ar(CDE)`
`ar(ABE)=ar(ACE)`
Proved.
Q2. In a triangle `ABC, E` is the mid-point of median `AD.` Show that `ar(BED)=1/4(ar(ABC).`
Sol. :
`triangleABC`, `AD` is median and `E` is the midpoint of `AD`.
To Prove:
`ar(BED)=1/2ar(ABC)`
Proof:
In `triangleABC`,
`AD` is the median
`ar(ADB)=ar(ACD)`
`ar(ADB)=1/2(ABC)`__________(1)
In `triangleADB`
`E` is the midpoint of `AD`,
`BE` is the median of `triangleADB`
`ar(BED)=1/2ar(ADB)`________(2)
from equation (1) and (2)
`ar(BED)=1/2times1/2(ABC)`
`ar(BED)=1/4ar(ABC)`.
Proved.
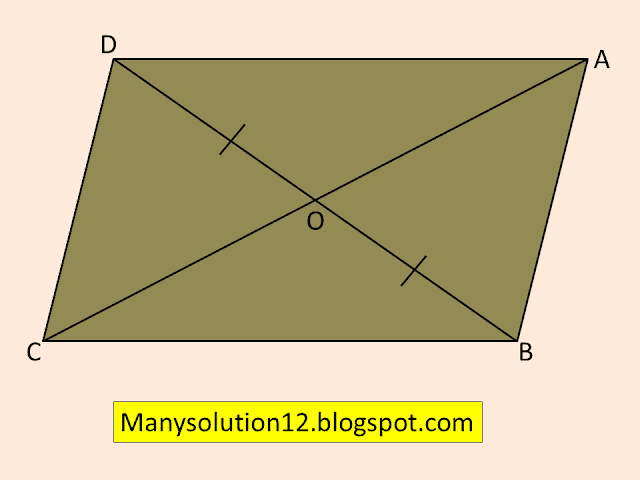
Q3. Show that the diagonals of a parallelogram divide it into four triangles of equal area.
Sol.
Given:
`▱ABCD`
To Prove:
`ar(AOB)=ar(BOC)=ar(COD)=ar(DOA)`
Proof:
In `triangleABD`, `OA` is the median
`ar(AOB)=ar(AOD)`_________(1)
In `triangleABC`, `OA` is the median
`ar(AOB)=ar(BOC)`_________(2)
In `triangleBCD`, `OC` is the median
`ar(BOC)=ar(COD)`_________(3)
from equation (1), (2), and (3)
`ar(AOB)=ar(BOC)=ar(COD)=ar(DOA)`
Proved.
Q4. In Figure, `ABC` and `ABD` are two triangles on the same base `AB.` If line segment `CD` is bisected by `AB` at `O,` show that `ar(ABC)=ar(ABD).`
Sol. :
Given:
`triangleABC` and `triangleABD` both have same base `AB`,
`OC=OD`
To Prove:
`ar(ABC)=ar(ABD)`
Proof:
`OC=OD`, `O` is the midpoint of `CD`
In `triangleACD`, `AO` is the median
`ar(AOC)=ar(AOD)`_______(1)
In `triangleBCD`, `OB` is the median
`ar(BOC)=ar(BOD)`________(2)
We Add equation (1) and (2)
`ar(AOC)+ar(BOC)=ar(AOD)+ar(BOD)`
`ar(ABC)=ar(ABD)`
Proved.
Q5. `D, E` and `F` are respectively the mid-points of the sides `BC, CA` and `AB` of a `triangleABC.`Show that
i) `BDEF` is a parallelogram.
ii) `ar(DEF)=1/4ar(ABC)`
iii) `ar(BDEF)=1/2 ar(ABC)`
Sol. :
Given:
`triangleABC,` `D,` `E,` `F` are midpoint of side `BC`, `CA`, and `AB`.
To Prove:
i) `BDEF` ia a parallelogram.
ii) `ar(DEF)=1/4ar(ABC)`.
iii) `ar(BDEF)=1/2(ABC)`.
Proof:
i) In `triangleABC`, `F` and `E` are the midpoint of sides `AB` and `CA`.
`EF∥BC` or `FE∥BD`
`D` and `E` are the midpoint of sides `BC` and `CA`
`DE∥BA` or `DE∥BF`
`BDEF` is a parallelogram.
Proved.
ii) Daigonal `DF` divide parallelogram `BDEF` into two triangle `BDF` and `DEF` of equal area.
similarly
`ar(AEF)+ar(BDF)+ar(CDE)+ar(DEF)=ar(ABC)`
`4ar(DEF)=ar(ABC)`
`ar(DEF)=1/4ar(ABC)`
Proved.
iii) Diagonal divide parallelogram into two triangle of equal area.
`ar(BDF)=ar(DEF)`
`ar(BDEF)=ar(BDF)+ar(DEF)`
`ar(BDEF)=2ar(DEF)`
`ar(BDEF)=2times1/4ar(ABC)`
`ar(BDEF)=1/2ar(ABC)`
Proved.
Q6. In Figure, diagonals `AC` and `BD` of quadrilateral `ABCD` intersect at `O` such that `OB=OD.` If `AB=CD,` then show that:i) `ar(DOC)=ar(AOB)`
ii) `ar(DCB)=ar(ACB)`
iii) `DA∥CB` or `AB⊥CD` is a parallelogram.
[Hint: From `D` and `B,` draw perpendiculars to `AC`]
Given:
`▱ABCD`, `OB=OD`,and `AB=CD`
To prove:
i) `ar(DOC)=ar(AOB)`
ii) `ar(DCB)=ar(ACB)`
iii) `DA∥CB` or `AB⊥CD` is a parallelogram.
Construaction:
Draw `(DE)`and `(BF)` perpendicular from point `D`, and `B` on `AC`.
Proof.
i) Draw `DN⊥AC` and `BM⊥AC`
In `triangleDNO` and `triangleBOM`
`angleDNO=angleBMO=90^circ` [By construction]
`angleDON=angleBOM` [Vertically opposite angles]
`OD=OB` [Given]
`triangleDONcongtriangleBOM`____(1) [By `A``A``S` rule]
`DN=BM`[By CPCT]
In `triangleDNC` and `triangleBMA`
`angleDNC=angleBMA=90^circ` [By construction]
`DC=AB` [ Given]
`DN=BM` [from proved (i)]
`triangleDNCcongtriangleBAM`_______(2)[By `RHS` rule]
We Add equation (1) and (2)
`ar(DON)+ar(DCN)=ar(BOM)+ar(BAM)`
`ar(DOC)=ar(AOB)`
Proved.
ii) `ar(DOC)=ar(AOB)`
We Add `ar(BOC)` both sides
`ar(DOC)+ar(BOC)=ar(BOM)+ar(BOC)`
`ar(DCB)=ar(ACB)`.
Proved.
iii) `triangleDCB` and `triangleACB` both have equal areas and the same base `BC`. So that `triangle`s
are lie between the same parallels `AD` and `BC`.
then `DA∥CB` so that `ABCD` is a parallelogram.
Proved.
Q7. `D` and `E` are points on sides `AB` and `AC` respectively of `triangleABC` such that `ar(DBC)=ar(EBC).` Prove that `DE∥BC.`
Sol. :
`triangleDCB` and `triangleEBC` both have same base `BC` and equal area. So that they will lies between the same parallels `DE` and `BC`.
`DE∥BC`
Proved.
Q8. `XY` is a line parallel to side `BC` of a triangle `ABC.` If `BE∥AC` and `CF∥AB` meet `XY` at `E` and `F` respectively, show that `ar(ABE)=ar(ACF)`Sol. :
Given:
`XY∥BC`, `BE∥AC` and `CF∥AB`
To Prove:
`ar(ABE)=ar(ACF)`
Proof:
In quadrilateral `ACBE`,
`AE∥CB` [ `BC∥XY`]
`AC∥BE` [ Given ]
`ACBE` is a parallelogram.
Similarly
`ABCF` is a parallelogram.
parallelogram `ABCF` and parallelogram `ACBE` both have same base `BC` and between the same parallel `BC` and `XY`
`ar(ACBE)=ar(ABCF)`
`ar(ABE)+ar(ABC)=ar(ABC)+ar(ACF)`
`ar(ABE)=ar(ACF)`
Proved.
Q9. The side `AB` of a parallelogram `ABCD` is produced to any point `P.` A line through `A` and parallel to `CP` meets `CB` produced at `Q` and then parallelogram `PBQR` is completed (see Figure). Show that `ar(ABCD)=ar(PBQR).`[Hint: Join `AC` and `PQ.` Now compare `ar(ACQ)` and `ar(APQ).`]
Given:
`ABCD` and `BPRQ` are parallelograms,
`CP∥AQ`
To Prove:
`ar(ABCD)=ar(BPRQ)`
Construction:
Join `AC` and `PQ`.
Proof:
`triangleACQ` and `triangleAPQ` both have same base `AQ` and are between the same parallels `AQ` and `CP`.
`ar(ACQ)=ar(APQ)`
`ar(ABQ)+ar(ABC)=ar(ABQ)+ar(BQC)`
`ar(ABC)=ar(BQC)`________(1)
`triangleABC` and `▱ABCD` both have same base `AC` and are between the same parallels `DC` and `AB`.
`ar(ABC)=1/2ar(ABCD)`______(2)
`triangleBQC` and `▱PBQR` both have same base `BQ` and are between the same parallels `BQ` and `PR`
`ar(BQC)=1/2ar(PBQR)`______(3)
from equation (1), (2) and (3)
`1/2ar(ABCD)=1/2ar(PBQR)`
`ar(ABCD)=ar(PBQR)`
Proved.
Or
Alternative Method
Given:
`ABCD` and `BPRQ` are parallelograms,
`CP∥AQ`
To Prove:
`ar(ABCD)=ar(BPRQ)`
Construction:
Join `AC` and `PQ`.
Proof:
`triangleACQ` and `triangleAPQ` both have same base `AQ` and are between the same parallels `AQ` and `CP`.
`ar(ACQ)=ar(APQ)`
`ar(ABQ)+ar(ABC)=ar(ABQ)+ar(BQP)`
`ar(ABC)=ar(BQP)`________(1)
We multiply by `2` both sides
`ar(ABC)=ar(BQP)`
`ar(ABCD)=ar(PBQR)` [Both are parallelogram]
Proved.
Q10. Diagonals `AC` and `BD` of a trapezium `ABCD` with `AB∥DC` intersect each other at `O.` Prove that `ar(AOD)=ar(BOC).`
Sol. :
Given:
`ABCD` is a trapezium, `AB∥DC`
To Prove:
`ar(AOD)=ar(BOC)`
Proof:
`triangleADC` and `triangleBCD` both have same base `CD` and between the same parallels `AB` and `CD`.
`ar(ADC)=ar(BCD)`
Subtracting `ar(DOC)` from both sides
`ar(ADC)-ar(DOC)=ar(BCD)-ar(DOC)`
`ar(AOD)=ar(BOC)`
Proved.
Q11. In Figure, `ABCDE` is a pentagon. A line through `B` parallel to `AC` meets `DC` produced at `F.` Show that ii) `ar(AEDF)=ar(ABCDE)`
Given:
`ABCDE` is pentagon.
To Prove:
i) `ar(ACB)=ar(ACF)`
ii) `ar(AEDF)=ar(ABCDE)`
Proof:
i) `triangleACB` and `triangleACF` both have same base `AC` and between the same parallels `AC` and `BF`.
`ar(ACB)=ar(ACF)`
Proved.
ii) We Add `ar(AEDC)` on both sides
`ar(ACB)+ar(AEDC)=ar(ACF)+ar(AEDC)`
`ar(ABCDE)=ar(AEDF)`
Proved.
Q12. A villager Itwaari has a plot of the shape pf a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amouint of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Sol. :
Given:
`ABCD` is a quadrilateral.
Construction:
Draw `DE∥CA` which intersect `BA` produced at `E`.
To Prove:
`ar(ABCD)=ar(EBC)`
Proof:
`triangleADC` and `triangleACE` both have same base `AC` and between the same parallels `AC` and `DE`
`ar(ADC)=ar(ACE)`
We Add `ar(ABC)` both sides.
`ar(ADC)+ar(ABC)=ar(ACE)+ar(ABC)`
`ar(ABCD)=ar(EBC)`
Proved.
Q13. `ABCD` is a trapezium with `AB∥DC. A `line parallel to `AC` intersects `AB` at `X` and `BC` at `Y`. Prove that `ar(ADX)=ar(ACY).`[Hint: Join `CX`.]
Sol. :
Given:
`ABCD` is a trapezium, `AB∥DC` and `AC∥XY`.
To Prove:
`ar(ADX)=ar(ACY)`
Construction:
Join `CX`.
Proof:
`triangleACX` and `triangleADX` both have same base `AX` and between the same parallel `AB` and `DC`.
`ar(ACX)=ar(ADX)`________(1)
`triangleACX` and `triangleACY` both have same base `AC` and between the same parallel `AC` and `XY`.
`ar(ACX)=ar(ACY)`________(2)
from equation (1) and (2)
`ar(ADX)=ar(ACY)`
Proved.
Q14. In Figure, `AP∥BQ∥CR.` Prove that `ar(AQC)=ar(PBR).`Given:
`AP∥BQ∥CR`
To Prove:
`ar(AQC)=ar(PBR)`
Proof:
`triangleABQ` and `trianglePBQ` both have same base `BQ` and between the same parallels `AP` and `BQ`.
`ar(ABQ)=ar(PBQ)`____________(1)
`triangleBCQ` and `triangleBQR` both have same base `BQ` and between the same parallels `CR` and `BQ`
`ar(BCQ)=ar(BQR)`____________(2)
We Add equation (1) and (2)
`ar(ABQ)+ar(BCQ)=ar(PBQ)+ar(BQR)`
`ar(AQC)=ar(PBQ)`
Proved.
Q15. Diagonals `AC` and `BD` of a quadrilateral `ABCD` intersect at `O` in such a way that `ar(BDP)=ar(ARC).` Prove that `ABCD` is a trapezium.Sol. :
`ar(AOD)=ar(BOC)`
To Proved:
`ABCD` is a trapezium.
Proof:
`ar(AOD)=ar(BOC)` [Given ]
We Add `ar(AOB)` both sides
`ar(AOD)+ar(AOB)=ar(BOC)+ar(AOB)`
`ar(BAD)=ar(ABC)`
`triangleBAD` and `triangleABC` both have same base `AB` and both have equal area.
these triangles lie between the same parallels
`AB∥DC`
So that `ABCD` is a trapezium.
Proved.
Q16. In Figure, `ar(DRC)=ar(DPC)` and `ar(BDP)=ar(ARC). `Show that both the quadrilaterals `ABCD` and `DCPR` are trapezium.
`ar(DRC)=ar(DPC)` and
`ar(BDP)=ar(ARC)`
To Prove:
`ABCD` and `DCPR` are trapezium.
Proof:
`triangleDCR` and `triangleDPC` both have the same base `DC` and equal area
these triangles lie between the same parallels
`DC∥RP`
So that `DCPR` is a trapezium.
`ar(BDP)=ar(ACR)`_______(1) [Given]
`ar(DPC)=ar(DRC)`_______(2) [Given]
Subtracting equation (1) and (2)
`ar(BDP)-ar(DPC)=ar(ACR)-ar(DRC)`
`ar(BDC)=ar(ADC)`
`triangleADC` and `triangleBDC` both have same base `DC` and have equal area.
these triangles lie between the same parallels
`AB∥DC`
So that `ABCD` is a trapezium.

















Comments