9th Maths 9.2
NCERT Class 9th solution of Exercise 9.1
NCERT Class 9th solution of Exercise 9.3
Exercise 9.2
Q1. In Figure, `ABCD` is a parallelogram, `AE⊥DC` and `CF⊥AD`. If `AB=16` cm, `AE=8` cm. and `CF=10` cm. Find `AD`.
Area of a parallelogram = Base`times`Height
Area of a parallelogram `ABCD=ADtimesAE`
Area of a parallelogram `ABCD=(16times8)cm^2 = 128cm^2`______(1)
Area of a parallelogram `ABCD=ADtimesCF`
Area of a parallelogram `ABCD=(ADtimes10)cm^2`______________(2)
From equation (1) and (2)
`128=ADtimes10`
`AD=128/10=12.8cm`
Answer:
`AD=12.8cm`.
Q2. If `E,F,G` and `H` are respectively the mid-points of the sides of a parallelogram `ABCD`, show that `ar(EFGH)=1/2ar(ABCD).`
Sol. :
Construction:
Join `HF`.
Proof:
In `triangleHGF` and parallelogram `HDCF` lies on the same base `HF` and lie between the same parallels `HF` and `DC`.
`ar(HGF)=1/2ar(HDCF)`_________(1)
In `triangleHEF` and parallelogram `ABFH` lies on the same base `HF` and lie between the same parallels `HF` and `AB`.
`ar(HEF)=1/2ar(ABFH)`_________(2)
By Adding equation (1) and (2)
`ar(HGE)+ar(HEF)=1/2[ar(HDCF)+ar(ABFH)]`
`ar(EFGH)=1/2ar(ABCD)`
Proved.
Q3. `P` and `Q` are any two points lying on the sides `DC` and `AD` respectively of a parallelogram `ABCD.` Show that `ar(APB)=ar(BQC).`
Sol. :
In `triangleAPB` and parallelogram `ABCD` lies on the same base `AB` and lie between the same parallels `AB` and `DC`.
`ar(APB)=1/2ar(ABCD)`_________(1)
In `triangle(BQC)` and parallelogram `ABCD` lies on the same base `AB` and lie between the same parallels `BC` and `AD`.
`ar(BQC)=1/2ar(ABCD)`____(2)
By equation (1) and (2)
`ar(APB)=ar(BQC)`.
Proved.
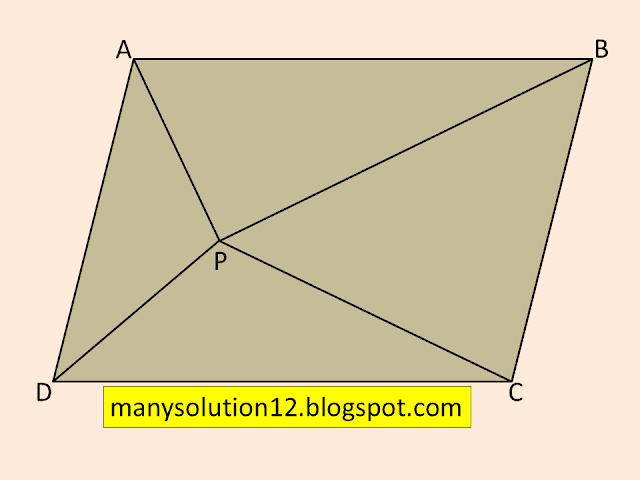
Q4. In Figure, `P` is a point in the interior of a parallelogram `ABCD`
i) `ar(APB)+ar(PCD)=1/2ar(ABCD)`
ii) `ar(APD)+ar(PBC)=ar(APB)+ar(PCD)`
[Hint: Though `P`, draw a line parallel to `AB.`]
i) Construction : Draw `EPF` parallel to `AB` or `DC` and `GPH` parallel to `AD` or `BC`.
Proof:
In `triangleAPB` and parallelogram `ABFE` lies on the same base `AB` and lie between the same paralled the same parallels `AB` and `DC`.
`ar(APB)=1/2ar(ABFE)`________(1)
and
`ar(PCD)=1/2ar(EFCD)`_________(2)
By Adding equation (1) and (2)
`ar(APB)+ar(PCD)=1/2ar(ABEF)+1/2ar(EFCD)`
`ar(APB)+ar(PCD)=1/2[ar(ABEF)+(EFCD)]`
`ar(APB)+ar(PCD)=1/2ar(ABCD)`_________(3)
ii) Proof:
In `triangleAPD` and parallelogram `AGHD` lies on the same base `AD` and lie between the same parallels `AD` and `HG`.
`ar(APD)=1/2ar(AGHD)`____________(4)
and
`ar(PCB)=1/2ar(GBCH)`_____________(5)
By Adding equation (4) and (5)
`ar(APD)+ar(PCB)=1/2ar(AGHD)+1/2ar(GBCH)`
`ar(APD)+ar(PCB)=1/2[ar(AGHD)+ar(GBCH)]`
`ar(APD)+ar(PCB)=1/2ar(ABCD)`______(6)
from equation (3) and (6)
`ar(APD)+ar(PBC)=ar(APB)+ar(PCD)`.
Proved.
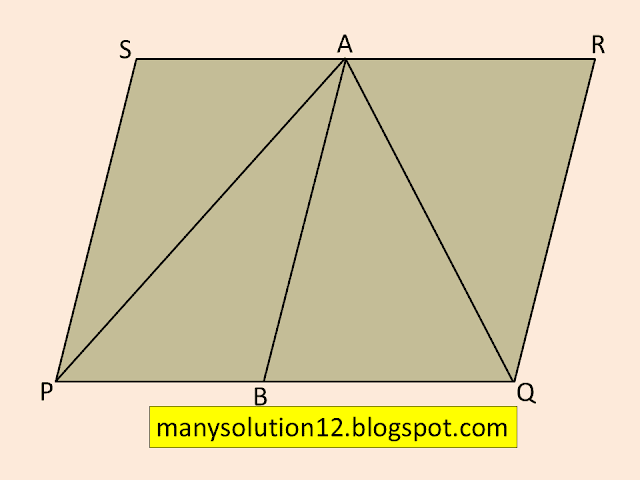
Q5. In Figure, `PQRS` and `ABRS` are parallelograms and `X` is any point on side `BR.` Show that
i) `ar(PQRS)=ar(ABRS)`
ii) `ar(AXS)=1/2ar(PQRS)`
i) Proof:
Parallelogram `PQRS` and parallelogram `ABRS` lies on the same base `RS` and lie between the same parallels `SR` and `PAQB`
`ar(PQRS)=ar(ABRS)`________(1)
ii) Proof:
In `triangleAXS` and parallelogram `ABRS` lies on the same base `AS` and lie between the same parallels `AS` and lie between the same parallels `AS` and `RS`.
`ar(AXS)=1/2ar(ABRS)`_______(2)
From equation (1) and (2)
`ar(AXS)=1/2ar(PQRS)`
Proved.
Q6. A farmer was having a field in the form of a parallelogram `PQRS.` She took any point `A` on `RS` and joined it to points `P` and `Q.` In how many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?
Sol. :
Parallelogram `PQRS`
To Prove:
`ar(APQ)=ar(APS)+ar(AQR)`
Construction:
Draw a line `AB` parallel to `SP`.
Proof:
In `triangleAPQ` and parallelogram `PQRS` are on the same base `PQ` and between the same parallels `PQ` and `RS`
`ar(APQ)=1/2ar(PQRS`
`2ar(APQ)=ar(PQRS)`
`2ar(APQ)=ar(APS)+ar((APQ)+ar(AQR)`
`2ar(APQ)-ar(APQ)=ar(APS)+ar(AQR)`
`ar(APQ)=ar(APS)+ar(AQR)`
Proved.
Comments