9th Maths 11.1

NCERT Class 9th solution of Exercise 11.1

NCERT Class 9th solution of Exercise 12.1

NCERT Class 9th Projects

Exercise 11.1

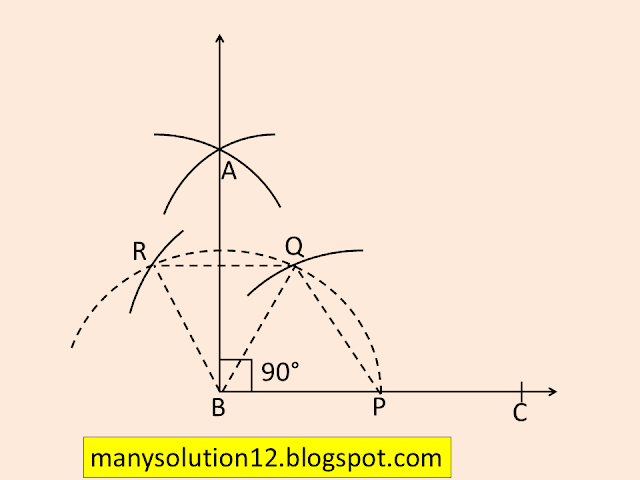
Q1. Construct an angle of `90^circ` at the initial point of a given ray and justify the construction.

Sol. :

Step of Construction:

1. Draw ray `BC`, take centre `B` draw an arc with any radius it intersects `BC` at `P`.
2. Take centre `P` draw arc with the same radius it intersects the previous arc at `Q`.
3. Take centre `Q` draw arc with the same radius it intersects the previous arc at `R`.
4. Take centres `Q` and `R` draw arcs with the same radius which intersects at `A`.
5. Join `AB`

this gives `angleABC=90^circ`.

Justification: 

`triangleBQP` is an equilateral triangle. [ By Construction]

`angleQBP=60^circ` [ Angle of the equilateral triangle]

`angleABQ=1/2angleQBP` [Ray `BA` is angle bisector]

`angleABQ=30^circ`

`angleABC=angleABQ+angleQBP`

`angleABC=30^circ+60^circ`

`angleABC=90^circ`.

hence Justified.

Q2. Construct an angle of `45^circ` at the initial point of a given ray and justify the construction.

Step of Construction:

1. Draw ray `BC`, take centre `B` draw an arc with any radius it intersects `BC` at `P`.
2. Take centre `P` draw arc with the same radius it intersects the previous arc at `Q`.
3.  Take centres `P` and `Q` draw arcs with the same radius which intersects at `R` 
4. Draw ray `BA` an angle bisector of `angleQBR`.

this gives `angleABC=45^circ`.

Justification:

`triangleBQP` is an equilateral triangle [ By Construction]

`angleQBP=60^circ` [ Angle of the equilateral triangle]

`angleRBC=angleABR=1/2angleQBC` [Ray `BR` is angle bisector]

`angleRBC=30^circ`

`angleABR=1/2angleRBC` [Ray `AB` is angle bisector]

`angleABC=angleARB+angleRBC`

`angleABC=15^circ+30^circ`

`angleABC=45^circ`

hence Justified.

Q3. Construct the angles of the following measurements:

    i) `30^circ`    ii) `22(1)/2^circ`    iii) `15^circ`

Sol. :

i) `30^circ`

Step of Construction:

1. Draw ray `BC`, take centre `B` draw an arc with any radius it intersects `BC` at `P`.
2. Take centre `P` draw arc with the same radius it intersects the previous arc at `Q`.
3. Draw angle bisector `BA` of `angleQBC`.
4. We get `angleABC=30^circ`.

ii) `22(1)/2^circ`

Step of Construction:

1. Draw ray `BC`, take centre `B` draw an arc with any radius it intersects `BC` at `P`.
2. Take centre `P` draw arc with the same radius it intersects the previous arc at `Q`.
3. Draw ray `BR` is the angle bisector of `angle QBC`.
4. Draw ray `BS` is the angle bisector of `angle RBC`.
5. Draw ray `BA` is the angle bisector of `angle RBS`.
6. We get `angleABC=22(1)/2^circ`.

iii) `15^circ`

Step of Construction:

1. Draw ray `BC`, take centre `B` draw an arc with any radius it intersects `BC` at `P`.
2. Take centre `P` draw arc with the same radius it intersects the previous arc at `Q`.
3. Draw ray `BR` is the angle bisector of `angleQBC`.
4. Draw ray `BA` is the angle bisector of `angleRBC`.
5. We get `angleABC=15^circ`.

Q4. Construct the following angles and verify by measuring them by a protractor:

    i) `75^circ`    ii) `105^circ`    iii) `135^cric`

Sol. :

i) `75^circ`

Step of Construction:

1. Draw ray `BC`, take centre `B` draw an arc with any radius it intersects `BC` at `P`.
2. Take centre `P` draw arc with the same radius it intersects the previous arc at `Q`.
3. Take centre `Q` draw arc with the same radius it intersects the previous arc at `R`.
4. Draw ray `BS` is the angle bisector of `angleRBQ`.
5. Draw ray `BA` is the angle bisector of `angleSBQ`.
6. We get `angleABC=75^circ`.

ii) `105^circ`

Step of Construction:

1. Draw ray `BC`, take centre `B` draw an arc with any radius it intersects `BC` at `P`.
2. Take centre `P` draw arc with the same radius it intersects the previous arc at `Q`.
3. Take centre `Q` draw arc with the same radius it intersects the previous arc at `R`.
4. Draw ray `BS` is the angle bisector of `angleQBR`.
5. Draw ray `BA` is the angle bisector of `angleRBS`.
6. we get `angleABC=105^circ`.

iii) `135^circ`

Step of Construction:

1. Draw line `SC`, take centre `B` draw an arc with any radius it intersects `SC` at `P` and `S`.
2. Take centre `P` draw arc with the same radius it intersects the previous arc at `Q`.
3. Take centre `Q` draw arc with the same radius it intersects the previous arc at `R`.
4. Draw ray `BT` is the angle bisector of `angleRBS`.
5. Draw ray `BA` is the angle bisector of `angleTBR`.
6. We get `angleABC=135^circ`.

Q5. Construct an equilateral triangle, given its side and justify the construction.

Sol. :

Step of Construction:

1. Draw line segment `BC`.
2. Take centres `B` and `C` draw an arc with a radius equal to `BC` it intersects at `A`.
3. Join `AB` and `AC`.
4. We get `triangleABC`.

Justification:

`AB=BC=CA`

`triangleABC` is an equilateral triangle.