10th Maths12.2

Exercise 12.2

Unless stated otherwise, use

$pi = 22/7$ .

Q1. Find the area of a sector of a circle with radius

$text{6 cm}$ if angle of the sector is

$60^circ$ .

$text{Sol.}$

$text{Area of sector = }theta/{360^circ}times pi text{r}^2$

$text{ = }60^circ/{360^circ}times 22/7 times(6)^2$

$text{ = }(6times6)/6times22/7$

$text{ = }(6times22)/7$

$text{ = } 132/7text{ cm}^2$

$text{Answer}$

$text{Area of sector }132/7 text{ cm}^2.$

Q2. Find the area of a quadrant of a circle whose circumference is

$text{22 cm}$ .

$text{Sol.}$

$text{Circumference of the circle = }2pitext{r}$

$text{ 22 = }2times22/7timestext{r}$

$text{ r = }(2times22times7)/(2times22)$

$text{ r = }7/2$

$text{Area of Quadrant = }theta/{360^circ}times pi text{r}^2$

$text{ = }90^circ/{360^circ}times 22/7 times(7/2)^2$

$text{ = }1/4times(22times7)/4$

$text{ = }(77)/8$

$text{ = } 77/8text{ cm}^2$

$text{Answer}$

$text{Area of Quadrant = } 77/8text{ cm}^2$ .

Q3. The length of the minute hand of a clock is

$text{14 cm}.$ Find the area swept by the minute hand in

$text{5 minutes.}$

$text{Sol.}$

$text{Minute hand cover}$

$theta = 360/60times5 = 30^circ$

$text{Area cover in 5 minute =}theta/360^circpitext{r}^2$

$= 30^circ/{360^circ}times 22/7 (text{14})^2$

$= 154/3 text{ cm}^2$

$text{Answer}$

$text{Area cover in 5 minute = }154/3 text{ cm}^2.$

Q4. A chord of a circle of radius

$text{10 cm}$ subtends a right angle at the centre. Find the area of the corresponding : i) minor segment ii) major sector.(Use

$pi = 3.14$ )

$text{Sol.}$

$text{Area of minor sector = }theta/{360^circ}times pi text{r}^2$

$= 90^circ/360^circ times 3.14 (10)^2$

$= 1/4times3.14times100$

$= 78.5 text{ cm}^2$

$text{Area of triangle = }1/2timestext{base}timestext{height}$

$= 1/2times10times10 = 50text{ cm}^2$

$text{Area of minor segment}=78.5 - 50 = 28.5 text{ cm}$

$text{Answer}$

$text{Area of minor sector = }28.5 text{ cm}^2$

ii)

$text{Area of major sector = }(360^circ-theta)/{360^circ}times pi text{r}^2$

$= (360^circ-90^circ)/360^circ times 3.14 times(10)^2$

$= 270^circtimes3.14times 100$

$=235.5 text{ cm}^2$

$text{Answer}$

$text{Area of major sector = }235.5 text{ cm}^2$ .

Q5. In a circle of radius

$text{21 cm},$ an arc subtends an angle of

$60^circ$ at the centre. Find :

i) the length of the arc

ii) area of the sector formed by the arc

iii) area of the segment formed by the corresponding chord.

$text{Sol.}$

$text{Radius (r) = 21 cm,}$

$text{Angle }(theta) = 60^circ$

$text{The length of the arc = }theta/360^circ times 2 pi text{r}$

$= 60^circ/360^circ times 2 times 22/7 times 21$

$= 22 text{ cm}$

$text{Answer}$

$text{The length of the arc 22 cm.}$

ii)

$text{Area of a sector =} theta/360^circ times pi text{r}^2$

$text{A}_1 = 60^circ/360^circ times 22/7 (21)^2$

$= 231 text{ cm}^2$

$text{Aswer}$

$text{Area of a sector 231 cm}^2$ .

iii)

$text{Area of equilateral}triangle = sqrt3/4 (a)^2$

$text{A}_2 = sqrt3/4 (21)^2$

$= (441sqrt3)/4 text{cm}^2$

$text{Area of segment = A}_1 - text{A}_2$

$= [231 - (441sqrt3)/4 ]text{ cm}^2$

$text{Answer}$

$text{Area of segment = }[231 - (441sqrt3)/4] text{ cm}^2$ .

Q6. A chord of a circle of radius

$text{15 cm}$ subtends an angle of

$60^circ$ at the centre. Find the areas of the corresponding minor and major segments of the circle.

(Use

$pi = 3.14$ and

$sqrt3 = 1.732$ )

$text{Sol.}$

$text{Area of sector = }theta/360^circ pi text{r}^2$

$text{A}_1 = 60^circ/360^circ times 22/7 (15)^2$

$= 1/6 times 22/7 times 15 times 15$

$= 1.57 times 75$

$= 117.75 text{ cm}^2$

$text{Area of equilateral} triangle = sqrt3/4 (a)^2$

$text{A}_2 = sqrt3/4(15)^2$

$= (225sqrt3)/4$

$= 97.31 text{cm}^2$

$text{Area of minor segment = A}_1 - text{A}_2$

$= 117.75 - 97.31$

$= 20.44 text{ cm}^2$

$text{Area of the circle =} pi textr^2$

$text{A}_3 = 3.14 times (15)^2$

$= 3.14 times 225$

$= 706.5 text{ cm}^2$

$text{Area of major segment = A}_3 - (text{A}_1 - text{A}_2)$

$= 706.5 -20.44$

$= 686.06 text{ cm}^2$

$text{Answer}$

$text{Area of minor segment 20.44 cm}^2,$

$text{Area of major segment 686.06 cm}^2$ .

Q7. A chord of a circle of radius

$text{12 cm}$ subtends an angle of

$120^circ$ at the centre. Find the area of the corresponding segment of the circle.

(Use

$pi = 3.14$ and

$sqrt3 = 1.732$ )

$text{Sol.}$

$text{Area of sector = } theta/360^circ pi text{r}^2$

$text{A}_1= 120^circ/360^circ times 3,14 (12)^2$

$= 1/3 times 3.14 times 144$

$= 150.72 text{ cm}^2$

$text{In right }triangle text{AMO}$

$text{OM}/text{OA} = text{cos }angle text{AOM}$

$text{OM}/12 = text{cos }60^circ = 1/2$

$text{OM }= 1/2 times 12 = 6 text{cm}.$

$text{AM}/text{OA} = text{sin }angle text{MOA}$

$text{AM}/12 = text{sin }60^circ = sqrt3/2$

$text{AM } =sqrt3/2times12$

$= 6sqrt3 = 6 times 1.732 = 10.38 text{ cm}$

$text{AB } = 2text{AM }$

$= 2times 10.38 = 20.76$

$text{ar}(triangle text{BAO })= 1/2 times text{Base}times text{height}$

$= 1/2 text{AO}timestext{OM}$

$= 1/2 times 20.76times6$

$= 62.28 text{cm}^2$

$text{ar(segment BPA) = ar (OAPB) - ar(BAO)}$

$text{ar(BPA) = 150.72 - 62.28}$

$text{ar(BPA) = 88.44 cm}^2 text{ approx.}.$

$text{Answer}$

$text{Area of the segment 88.44 cm}^2$ .

Q8. A horse is tide to a peg at one corner of a square shaped grass field of side

$text{15 m}$ by means of a

$text{5 m}$ long rope (see figure).

Find

i) the area of that part of the field in which the horse can graze.

ii) the increase in the grazing area if the rope were

$text{10 m}$ long instead of

$text{5 m}$ .(Use

$pi = 3.14$ )

$text{Sol.}$

$text{When the length of rope (r) is 5 m and}$

$text{each corner of square shape has }(theta) = 90^circ.$

$text{The grazing area = }theta/360^circ times pi text{r}^2$

$text{A}_1= 90^circ/360^circtimes3.14(5)^2$

$text{ }= (3.14times25)/4$

$text{ }= 78.5/4$

$text{ }= 19.625text{ m}^2$

$text{Answer}$

$text{The grazing area 19.25 m}^2$ .

ii)

$text{When the length of rope (r) is 10 m and}$

$text{each corner of square shape has }(theta) = 90^circ.$

$text{The new grazing area = }theta/360^circ times pi text{r}^2$

$text{A}_2= 90^circ/360^circ times 3.14(10)^2$

$text{ }=(3.14times100)/4$

$text{ }=157/2$

$text{ }=78.50text{ m}^2$

$text{The increasing area}$

$text{ }=text{A}_2-text{A}_1$

$text{ }=78.50-19.625$

$text{ }=58.875text{ m}^2$

$text{Answer:}$

$text{The increasing area 58.875 m}^2$ .

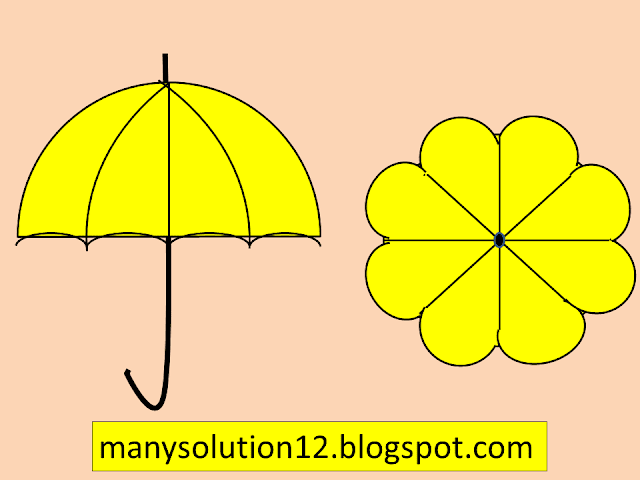
Q9. A brooch is made with silver wire in the form of a circle with diameter

$text{35 mm}$ . The wire is also used in making

$5$ diameters which divide the circle into

$10$ equal sectors as shown in Figure.

Find :

i) the total length of the silver wire required.

ii) the area of each sector of the brooch.

$text{Sol.}$

$text{Diameter of the circle (d) = 35 mm}$

$text{Circumference of the circle = 2}pitext{r}=pi text{d}$

$= 22/7times35$

$= 22times5$

$= 110 text{ mm.}$

$text{The length of wire used in 5 diameter}$

$= 5times35$

$=175 text{ mm}.$

$text{total length of the silver wire}$

$=110 + 175$

$=285 text{ mm}$ .

$text{Answer}$

$text{Total length of the silver wire 285 mm.}$

ii)

$text{Number of the equal sectors in the brooch = 10}$

$text{Radius of each sector (r)} = 35/2$

$text{Angle of the sector} theta =360/10 = 36$

$text{Area of each sector = }theta/360^circtimespitext{r}^2$

$= 36^circ/360^circtimes22/7(35/2)^2$

$= 1/10times22/7times35/2times35/2$

$= (41times35)/4$

$=385/4$

$text{Answer}$

$text{Area of each sector } 385/4 text{ mm}^2.$

Q10. An umbrella has

$8$ ribs which are equally spaced (see figure). Assuming umbrella to be a flat circle of radius

$text{45 cm},$ find the area between the two consecutive ribs of the umbrella.

$text{Sol.}$

$text{An umbrella with equally spaced ribs (sector),}$

$text{Radius is 45 cm,}$

$text{Angle of each sector }theta = 360^circ/8 = 45^circ$

$text{Area of each sector }= theta/360^circ pitext{r}^2$

$= 45^circ/360^circ times22/7 (45)^2$

$= 1/5 times 22/7 times 45 times 45$

$= 22275/28text{ cm}^2$

$text{Answer}$

$text{Area of each sector =} 22275/28 text{ cm}^2.$

Q11. A car has two wipers which do not overlap. Each wiper has a blade of length

$text{25 cm}$ sweeping through an angle of

$115^circ$ . Find the total area cleaned at each sweep of the blades.

$text{Sol.}$

$text{Length of each blade (radius) 25 cm,}$

$text{Angle of sector 115}^circ,$

$text{Total area of sector}$

$2 timestext{Area of each sector =}2 times theta/360^circ pi text{r}^2$

$= 2times115^circ/360^circ times 22/7 times (25)^2$

$= 23/18times11/7times625$

$= 158125/126 text{ cm}^2$

$text{Answer}$

$text{Total area of the sector =}158125/126 text{ cm}^2.$

Q12. To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle

$80^circ$ to a distance of

$text{16.5 km}$ . Find the area of the sea over which the ships are warned. (Use

$pi = 3.14$ )

$text{Sol.}$

$text{Radius of sector (r) = 16.5 km,$

$text{Angle of sector } (theta) = 80^circ$

$text{Area of sea cover by light},$

$text{Area of sector = }theta/360pitext{r}^2$

$= 80^circ/360^circ times3.14times(16.5)^2$

$= 189.97 text{ km}^2$

$text{Answer}$

$text{The area of sea is 189.97 km}^2.$

Q13. A round table cover has six equal designs as shown in figure. If the radius of the cover is

$text{28 cm}$ , find the cost of making the designs at the rate of

$text{0.35 per cm}^2.$ (Use

$sqrt3 = 1.7$ )

$text{Sol.}$

$text{Area of equilateral}triangle = sqrt3/4 times text{ a}^2$

$text{A}_1= sqrt3/4times (28)^2$

$= 333.2 text{ cm}^2$

$text{Area of a sector = } theta/360^circ times pi text{r}^2$

$text{A}_2 = 60^circ/360^circ times 22/7times (28)^2$

$= 1/6 times 22/7 times 28 times 28$

$= 410.67 text{ cm}^2$

$text{Area of a degisn = A}_2 - text{A}_1$

$= 410.67 - 333.2$

$= 77.47 text{ cm}^2$

$text{Total area of designs = }6 times text{Area of a design}$

$= 6 times 77.47 text{ cm}^2$

$= 464.82 text{ cm}^2$

$text{Cost of the designs = Area of a design }timestext{ Rate}$

$= 464.82 times 0.35$

$= text{ ₹ 162.68}$

$text{Answer}$

$text{Cost of the designs ₹ 162.68.}$

Q14. Tick the correct answer in the following :

Area of a sector of angle p (in degrees) of a circle with radius R is

$p/180 times 2 pi R$

$p/180 times pi R^2$

$p/360 times 2 pi R$

$p/720 times 2 pi R^2$

$text{Answer}$

$p/720 times 2 pi R^2$

Search This Blog

10th Maths12.2

NCERT Class 10th solution of Exercise 12.1

NCERT Class 10th solution of Exercise 12.3

NCERT Class 10th Maths Projects

Exercise 12.2

Comments

Popular posts from this blog

10th Maths Chapter 1

MPBSE 10th & 12th Result

CBSE 10th and 12th Result