9th Maths 10.4
NCERT Class 9th solution of Exercise 10.1
NCERT Class 9th solution of Exercise 10.2
NCERT Class 9th solution of Exercise 10.3
Exercise 10.4
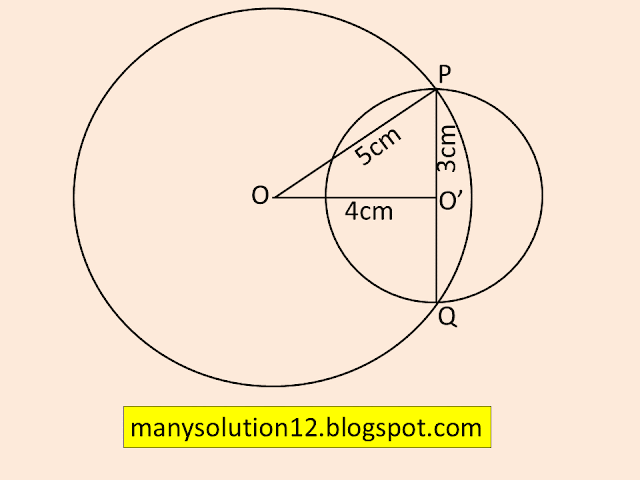
Q1. Two circles of radii `5cm` and `3cm` intersect at two points and the distance between their centres is `4cm`. Find the length of the common chord.
Sol. :
Let radius `OP=5cm`, `O'P=3cm`. The distance of `OO'` is `4cm`.
To Find:
`PQ`
Solve:
In `triangleOPO'
`(OP)^2=(OO')^2+(O'P)^2` [By Pythagoras Theorem]
`(5)^2=(4)^2+(3)^2`
`25=16+9`
`25=25`
`triangleOPO' is a right-angled triangle.
this gives `OO'⊥OP`
`PQ` is the diameter of the circle of radius `3cm` as it passes through centre `O'`.
`PQ=2times3=6cm`.
Answer:
The length of the common chord is `6cm`.
Q2. If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Sol. :
Given:
Chords `AB=CD` of a circle with centre `O` which intersect at `P`
To Prove:
`AP=PD` and `PB=PC`
Construction:
Draw `ON⊥CD` and `OM⊥AB`. Join `OP`.
Proof:
In `triangleOPM` and `triangleOPN`
`angleOMP=angleONP=90^circ` [By construction]
`OP=OP` [Common]
`OM=ON` [Equal chords are equidistance from the centre of circle]
`triangleOPMcongtriangleOPN` [By RHS rule]
`PM=PN`_________(1) [By CPCT]
`AB=CD` [Given]
`1/2AB=1/2CD`
`MB=CN`________(2)
`AM=ND`
Add equation (1) and (2)
`PM+AM=PN+ND`
`AP=PD`
Subtract equation (1) and (2)
`MB-PM=CN-PN`
`PB=PC`
Proved.
Q3. If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Sol. :
Given:
Chords `AB=CD` of a circle with centre `O` which intersect at `P`
To Prove:
`angleOPM=angleOPN`
Construction:
Draw `ON⊥CD` and `OM⊥AB`. Join `OP`.
Proof:
In `triangleOPM` and `triangleOPN`
`angleOMP=angleONP=90^circ` [By construction]
`OP=OP` [Common]
`OM=ON` [Equal chords are equidistance from the centre of circle]
`triangleOPMcongtriangleOPN` [By RHS rule]
`angleOPM=angleOPN` [By CPCT]
Proved.
Q4. If a line intersects two concentric circles (circles with the same centre) with centre `O` at `A,B,C` and `D,` prove that `AB=CD`[See figure]
Sol. :
Given:
Line intersect two concentric circles with centre `O` at `A, B, C, D.`
To Prove:
`AB=CD`
Construction:
Draw `OM⊥AD`
Proof:
Perpendicular `OM` from the centre of a circle to a chord `AD` bisects the chord.
`AM=DM`___________(1)
Perpendicular `OM` from the centre of a circle to a chord `BC` bisects the chord.
`BM=CM`___________(2)
Subtract equation (1) - (2)
`AM-BM=DM-CM`
`AB=CD`
Proved.
Q5. Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius `5m` drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and distance between Salma and Mandip is `6m` each, what is the distance between Reshma and Mandip?
Sol. :
`OR=OM=5m` and `SR=SM=6m`
To Find:
`MR`
Construction:
Join `OR, OM` and `OS=5cm`. `OL⊥SR`
Solve:
In `triangleORL,`
`(OR)^2=(OL)^2+(LR)^2` [By Pythagorus Theorem]
`(5)^2=(OL)^2+(3)^2`
`(OL)^2=25-9`
`(OL)^2=16`
`OL=4`
Area of `triangleROS=`Area of `triangleROS`
`1/2timesOStimesRN=1/2timesORtimesOL`
`1/2times5timesRN=1/2times6times4`
`RN=24/5`
`RN=4.8m`
`RM=2RN`
`RM=2times4.8=9.6m`
Answer:
The distance between Reshma and Mandip is `9.6m`.
Q6. A circular park of radius `20m` is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other . Find the length of the string of each phone.
Sol. :
radius `OA=OB=20m`,
`AS=SD=DA`
Construction:
Draw `AM⊥SD`, join `OS`.
Solve:
Let `AS=SD=DA=2x`, and `SM=MD=x`
In Right `triangleASM`
`(AS)^2=(SM)^2+(AM)^2`[By Pythagorus Theroem]
`(2x)^2=(x)^2+(AM)^2`
`4x^2=x^2+(AM)^2`
`(AM)^2=4x^2-x^2`
`(AM)^2=3x^2`
`AM=sqrt3x`
`OM=AM-OA`
`OM=(sqrt3x-20)m`__________(1)
In Right `triangleOSM`
`(OS)^2=(SM)^2+(OM)^2`
`(20)^2=(x)^2+(sqrt3x-20)^2` [from equation (1)]
`400=x^2+3x^2-2times20sqrt3x+400` [`(a-b)^2=a^2-2ab+b^2`]
`400-400=4x(x-10sqrt3x)`
`0=x-10sqrt3x`
`x=10sqrt3x`
`SD=2SM`
`SD=2x=2times10sqrt3m`
`SD=20sqrt3m`
`SD=20times1.732m`
`SD=34.640m`
Answer :
The length of the string of each phone is `34.640m.`








Comments