9th Maths 1.5

NCERT Class 9th solution of Exercise 1.1

NCERT Class 9th solution of Exercise 1.2

NCERT Class 9th solution of Exercise 1.3

NCERT Class 9th solution of Exercise 1.4

NCERT Class 9th solution of Exercise 1.6

NCERT Class 9th Maths Projects

Exercise 1.5 

Q1. Classify the following numbers as rational or irrational :

i) `2 - \sqrt5`

ii) (`3 - \sqrt23)  - \sqrt23` 

iii) `\frac{2\sqrt7}{7\sqrt7}`  iv) `\frac{1}{\sqrt2}`

v) `2π`

Answer :

Rational numbers : (ii) and (iii)

Irrational numbers : (i), (iv) and (v)

Q2. Simplify each of the following expression :

i)  (`3 + \sqrt3`)(`2 + \sqrt2`)

ii) (`3 + \sqrt3`)(`3 - \sqrt3`)

iii) `\(sqrt5 - sqrt2)^2`    

iv) (`\sqrt5 - \sqrt2`)(`\sqrt5 + \sqrt2`)

Sol. :

i) (`3 + \sqrt3`)(`2 + \sqrt2`) 

= `3 × 2 + 3\sqrt3 + 2\sqrt2`

    `+ \sqrt3\sqrt2`

= `6 + 3\sqrt3 + 2\sqrt2`

    `+ \sqrt6`

Answer :

= `6 + 3\sqrt3 + 2\sqrt2 + \sqrt6`

 ii) (`3 + \sqrt3`)(`3 - \sqrt3`)

=`\(3)^2-\(sqrt3)^2`

= `9 - 3`

= `6`

 Answer : 

`6`

iii) `\(sqrt5 - sqrt2)^2`  

= `(\sqrt5)^2 + 2\sqrt5\sqrt2 + \(sqrt2)^2`

= `5 + 2\sqrt10 + 2`

= `7 + 2\sqrt10`

Answer :

 = `7 + 2\sqrt10`

iv) (`\sqrt5 - \sqrt2`)(`\sqrt5 + \sqrt2`)

=`(sqrt5)^2 - (sqrt2)^2`

= `5 - 2`

= `3`

Answer :

= `3`

Q3. Recall `π` is defined as the ratio of the circumference (say c) of a circle to its diameter (say d) that is `π` = `frac{c}{d}`. This seems to contradict the fact that `π` is irrational. How will you resolve this contradiction?

Answer :

There is no contradiction (statement cannot be proven false). Remember that when you measure a length with a scale or any other device, you only get an approximate rational value. So, you may not realise that either c or d is irrational.

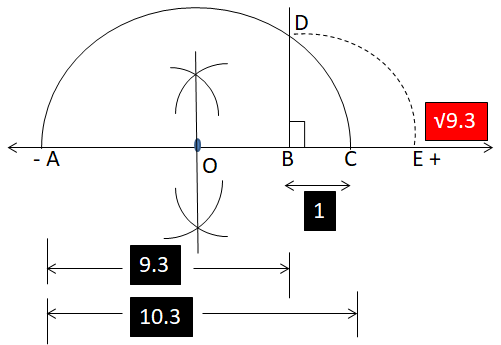
Q4. Represent `sqrt{9.3}` on the number line.

Sol. :

1) Draw a line segment AB = `9.3` units.

2) Extent AB to BC = `1` unit.

3) Find the mid-point of AC and mark that point as O.

4) Draw a semicircle with centre O and radius OC.

5) Draw a Perpendicular on B it intersects Semicircle at D.

6) Draw an arc with centre B and radius BD, it intersects a line at E. 

Thus point E represents `sqrt{9.3}`.

 Q5. Rationalise the denominators of the following :

i) `frac{1}{sqrt7}` ii) `frac{1}{sqrt7 - sqrt6}`  iii) `frac{1}{sqrt5 - sqrt2}` iv) `frac{1}{sqrt7 - 2}`

Sol. : 

i) `frac{1}{sqrt7}` 

=`frac{1}{sqrt7} × frac{sqrt7}{sqrt7}` 

=  `frac{sqrt7}{7}`

Answer : 

`frac{sqrt7}{7}`

ii) `frac{1}{sqrt7 - sqrt6}` 

= `frac{1}{sqrt7 - sqrt6} × frac{sqrt7 + sqrt6}{sqrt7 + sqrt6}` 

= `frac{sqrt7 + sqrt6}{7 - 6 }` 

= `sqrt7 + sqrt6`

Answer :

`sqrt7 + sqrt6`

iii) `frac{1}{sqrt5 + sqrt2}` 

=  `frac{1}{sqrt5 + sqrt2}×frac{sqrt5 - sqrt2}{sqrt5 - sqrt2}`

=  `frac{sqrt5 - sqrt2}{5 - 2}` 

=  `frac{sqrt5 - sqrt2}{3}`

Answer :

`frac{sqrt5 - sqrt2}{3}`

iv) `frac{1}{sqrt7 - 2}` 

= `frac{1}{sqrt7 - 2}×frac{1}{sqrt7 - 2}` 

= `frac{sqrt7 + 2}{7 - 4}` 

= `frac{sqrt7 + 2}{3}`

Answer :

`frac{sqrt7 + 2}{3}`