8th Maths 3.3

NCERT Class 8th solution of exercise 3.1

NCERT Class 8th solution of Exercise 3.2

NCERT Class 8th solution of Exercise 3.4

Exercise 3.3

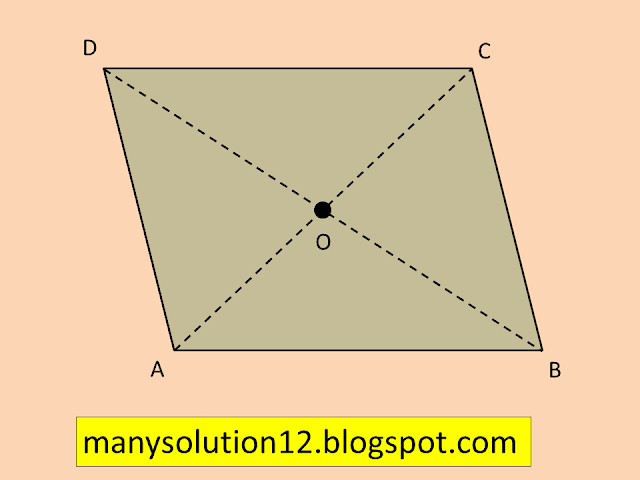
Q1. Given a parallelogram `text{ABCD}`. Complete each statement with the definition or property used.

i) `text{AD}` = ..........

ii) `angle text{DCB}` = ............

iii) `text{OC}` = ...........

iv) `m angle text{DAB} + m angletext{CDA}` = ..........

`text{Answer:}`

i) `text{BC (Opposite sides are equal)}`

ii) `angletext{DAB (Opposite angles are equal)}`

iii) `text{OA (Diagonals bisect each other)}`

iv) `180^circ text{(Interior opposite angles,}overline text{AB}∥ overline text{DC})`

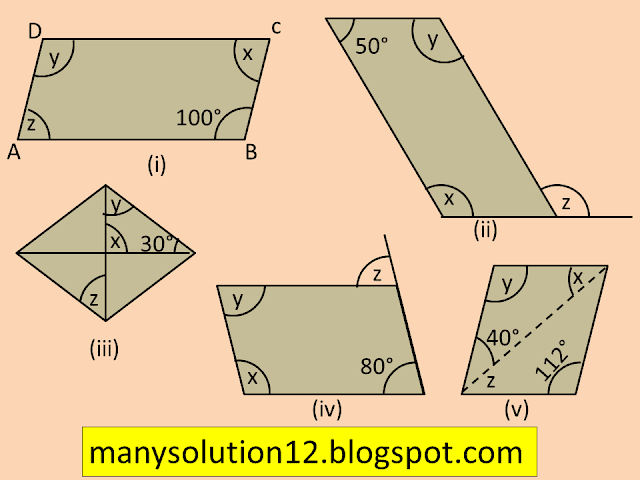
Q2. Consider the following parallelograms. Find the values of the unknowns `text{x, y, z}`

i)

`text{Sol.}`

`angle text{B} + angle text{C} = 180^circ text{ [adjacent angles]}`

`100^circ + text{x} = 180^circ`

`text{x} = 180^circ - 100^circ`

`text{x} = 80^circ`

`angle text{D} = angle text{B} text{ [opposite angles]}`

`text{y} = 100^circ`

`angle text{A} = angle text{C} text{ [opposite angles]}`

`text{z = x}`

`text{z} = 80^circ`

`text{Answer:}`

`text{x} = 80^circ, text{y} = 100^circ, text{z} = 80^circ`

ii)

`text{Sol.}`

`50^circ + text{x} = 180^circ text{ [adjacent angles]}`

`text{x} = 180^circ - 50^circ`

`text{x} = 130^circ`

`text{y  = x [ opposite angles]}`

`text{y} = 130^circ`

`text{z = x [corresponding angles]}`

`text{z} = 130^circ`

`text{Answer:}`

`text{x} = 130^circ, text{y} = 130^circ, text{z} = 130^circ`

iii)

`text{Sol.}`

`text{x} = 90^circ text{ [vertically opposite angles]}`

`text{angle sum property of triangle}`

`text{x + y + } 30^circ = 180^circ`

`90^circ + text{y} + 30^circ = 180^circ`

`text{y} + 120^circ = 180^circ`

`text{y} = 180^circ - 120^circ`

`text{y} = 60^circ`

`text{z = y [alternate angles]}`

`text{z} = 60^circ`

`text{Answer:}`

`text{x} = 90^circ, text{y} = 60^circ, text{z} = 60^circ`

iv)

`text{Sol.}`

`text{x} + 80^circ = 180^circ text{ [adjacent angles]}`

`text{x} = 180^circ - 80^circ`

`text{x} = 100^circ`

`text{y} = 80^circ text{ [opposite angles]}`

`text{z} = 80^circ text{ [ corresponding angles]}`    

`text{Answer:}`

`text{x} = 100^circ, text{y} = 80^circ, text{z} = 80^circ`

v)

`text{Sol.}`

`text{y} = 112^circ text{ [opposite angles]}`

`text{angle sum property of triangle}`

`text{x + y + }40^circ = 180^circ`

`text{x} + 112^circ + 40^circ = 180^circ`

`text{x} + 152^circ = 180^circ`

`text{x} = 180^circ - 152^circ`

`text{x} = 28^circ`

`text{z = x [alternate angles]}`

`text{z} = 28^circ`

`text{Answer:}`

`text{x} = 28^circ, text{y} = 112^circ, text{z} = 28^circ`

Q3. Can a quadrilateral `text{ABCD}` be a parallelogram if

i) `angletext{D} + angletext{B} = 180^circ`?

`text{Sol.}`

`text{Answer:}`

`text{Can be but need not be}.`

ii) `text{AB = DC = 8 cm, AD = 4 cm }`and `text{BC = 4.4 cm}`?

`text{Sol.}`

`text{In a parallelogram, opposite sides are equal,}``text{but here AD}ne text{BC}.`

`text{Answer:}`

`text{No}`. 

iii) `angle text{A =70}^circ` and `angle text{C = 65}^circ`?

`text{Sol.}`

`text{In a parallelogram, opposite angles are equal, }``text{but here, }angle text{A}ne angle text{C}.` 

`text{Answer:}`

`text{No.}` 

Q4. Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.

`text{Sol.}`

`text{Answer:}`

`text{A kite, for example.}`

Q5. The measures of two adjacent angles of a parallelogram are in the ratio `3 : 2`. Find the measure of each of the angles of the parallelogram.

`text{Sol.}`

`text{Let first angle is 3x}`

`text{and second angle is 2x}`

`text{Sum of two adjacent angles of a}``text{parallelogram are 180}^circ`

`text{3x + 2x = }180^circ`

`text{5x} = 180^circ`

`text{x} = 180^circ/5`

`text{x} = 36^circ`

`text{3x =} 3times36^circ = 108^circ`

`text{2x =} 2times36^circ = 72^circ` 

`text{Answer:}`

`108^circ, 72^circ`.

Q6.Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.

`text{Sol.}`

`text{Let first angle is x}`

`text{and second angle is x}`

`text{Sum of two adjacent angles of a}``text{parallelogram are 180}^circ`

`text{x + x =}180^circ`

`text{2x} = 180^circ`

`text{x} = 180^circ/2`

`text{x} = 90^circ`

`text{Each angle measures }90^circ`

`text{Answer:}`

`text{Each is a right angle.}`

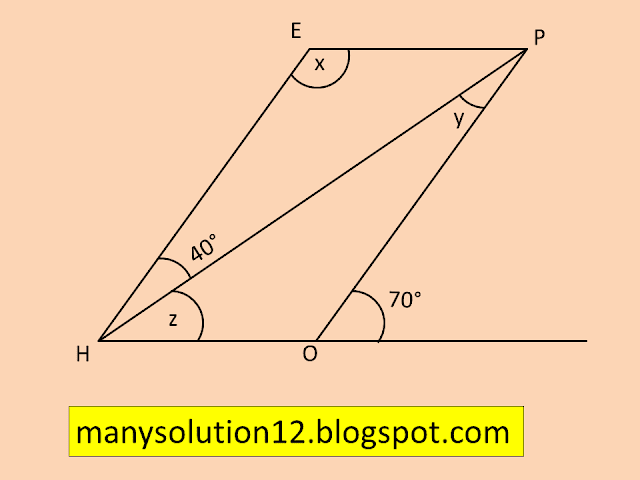
Q7. The adjacent figure `text{HOPE}` is a parallelogram. Find the angle measures `x, y,` and `z`. State the properties you use to find them.

`text{Sol.}`

`angle text{EHO =}70^circ text{[Corresponding angles]}`

`70^circ + text{x} =180^circ text{[adjacent angles]}`

`text{x}= 180^circ - 70^circ` 

`text{x}= 110^circ`

`text{y}= angle text{EHO [alternate angles]}`

`text{y} = 40^circ`

`angle text{EHO = }70^circ text{[Corresponding angles]}`

`angle text{EOP }+ angle text{PHO =}70^circ`

`40^circ + z = 70^circ`

`z = 70^circ - 40^circ`

`z = 30^circ`

`text{Answer:}`

`text{x} = 110^circ, text{y} = 40^circ, text{z} = 30^circ`.

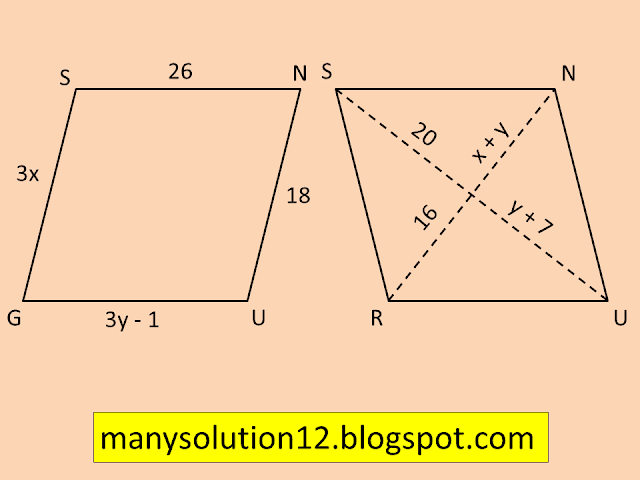
Q8. The following figures `text{GUNS}` and `text{RUNS}` are parallelograms.

Find `x` and `y`. (Lengths are in cm)

`text{Sol.}`

`text{GUNS}`

`text{3x = 18 [opposite sides of parallelogram]}`

`text{x} =18/3`

`text{x} = 6`

`text{3y - 1 = 26 [opposite sides of parallelogram]}`

`text{3y = 26 + 1}`

`text{y} = 27/3`

`text{y} = 9`

`text{Answer:}`

`text{x = 6, y = 9}`

`text{Sol.}`

`text{RUNS}`

`text{The diagonals of a parallelogram bisect}``text{each other}`

`text{y + 7 = 20}`

`text{y = 20 - 7}`

`text{y = 13}`

`text{and}`

`text{x + y = 16}`

`text{x + 13 = 16}`

`text{x = 16 - 13}`

`text{x = 3}`

`text{Answer:}`

`text{x = 3, y = 13}`

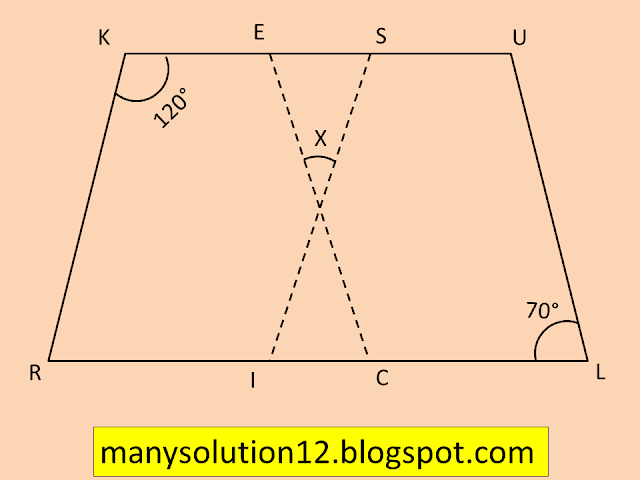
Q9. In the above figure both `text{RISK}` and `text{CLUE}` are parallelograms. Find the value of `x`.

`text{Sol.}`

`text{RISK}`

`angle text{K} + angle text{S} = 180^circ text{[adjacent angles]}`

`120^circ + angle text{S} = 180^circ`

`angle text{S} = 180^circ - 120^circ`

`angle text{S} = 60^circ`

`text{and}`

`text{CLUE}`

`angle text{E} = angle text{L [opposite angles]}`

`angle text{E} = 70^circ`

`text{Now}`

`text{Angle sum property of triangle}`

`text{x}+ 70^circ + 60^circ = 180^circ`

`text{x}+ 130^circ = 180^circ`

`text{x} = 180^circ - 130^circ`

`text{x} = 50^circ`

`text{Answer:}`

`text{x} = 50^circ`.

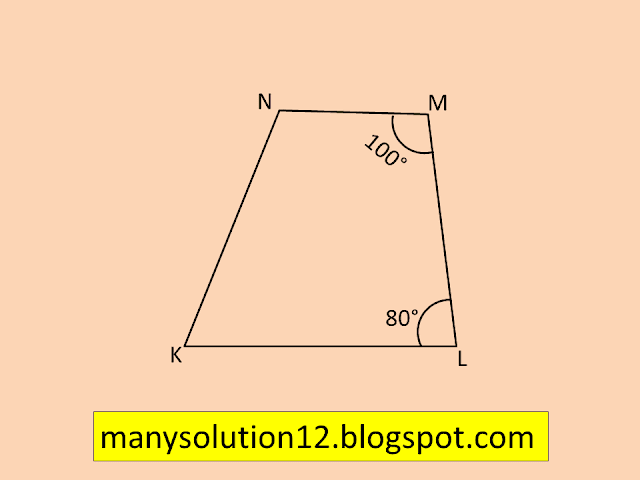
Q10. Explain how this figure is a trapezium. Which of its sides are parallel? (Fig.)

`text{Sol.}`

`text{Answer:}`

`overline text{NM}∥ overline text{KL} text{ (sum of interior opposite}``text{ angles is}` `180^circ).``text{So, KLMN is a trapezium.}`

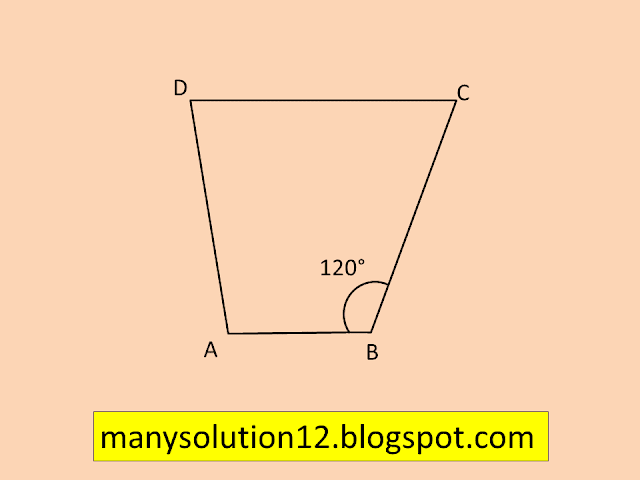
Q11. Find `m angletext{C}` in Fig. if  `overline text{AB} ∥ overline text{DC}`.

`text{Sol.}`

`angle text{B} + angle text{C} = 180^circ [ overline text{AB}∥ overline text{DC}]`

`120^circ + angle text{C} = 180^circ`

`angle text{C} = 180^circ - 120^circ`

`angle text{C} = 60^circ`

`text{Answer:}`

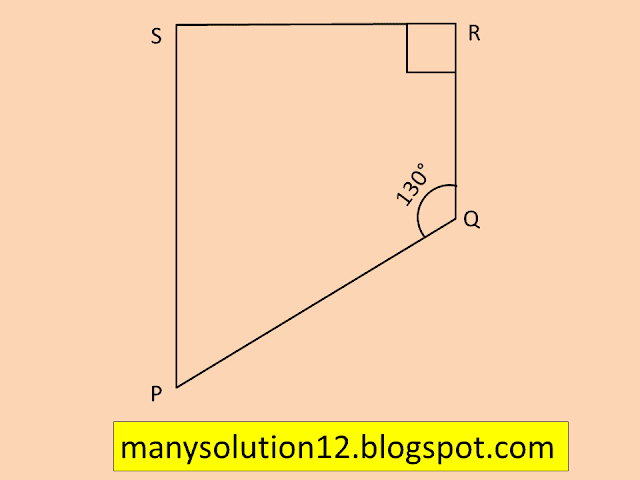
`60^circ`.

Q12. Find the measure of `angletext{P}` and `angle text{S}` if `overline text{SP} ∥ overline text{RQ}` in Fig. (If you find `mangle text{R}`, is there more than one method to find `mangletext{P}`?)

`text{Sol.}`

`angle text{P} + angle text{Q} = 180^circ [overline text{SP} ∥ overline text{RQ}]`

`angle text{P} + 130^circ = 180^circ`

`angle text{P} = 180^circ - 130^circ`

`angle text{P} = 50^circ`

`text{and}`

`angle text{S} + angle text{R} = 180^circ [overline{SP}∥ overline text{RQ}]`

`angle text{S} + 90^circ = 180^circ`

`angle text{S} = 180^circ - 90^circ`

`angle text{S} = 90^circ` 

`text{Answer:}`

`angle text{P} = 50^circ, angle text{S} = 90^circ`.